6.7机器学习期末复习题
空间
样本空间
就是属性的所有可能情况,包括了一切可能出现或不可能出现的所有样本情况
版本空间&假设空间
假设空间就是在样本空间的基础上,给所有属性都加了一个通配符,表示任意即可;以及加上了一个空集,表示该命题完全不成立
然后就相乘
然后对于版本空间,就是在假设空间里只保存那些符合训练集规定的正例假设的样本,所以就是不断从树顶开始往下删除
对于1,2,3,4组成的训练集,就是从原来的树顶不断删掉符合坏瓜定义的假设,直到全部删完
留出法

就是要保持分层采样
贝叶斯分类器

就是求后验概率,即已知特征是sunny,然后选手的类别是yes or no,即P(yes|sunny)
相关文章:

6.7机器学习期末复习题
空间 样本空间 就是属性的所有可能情况,包括了一切可能出现或不可能出现的所有样本情况 版本空间&假设空间 假设空间就是在样本空间的基础上,给所有属性都加了一个通配符,表示任意即可;以及加上了一个空集,表示…...

1123--日期类
目录 一 java 1. Date类 2. calendar类 3. 第三代日期类‘ 3.1 常用方法 3.2 格式化操作 一 java 1. Date类 2. calendar类 3. 第三代日期类‘ 3.1 常用方法 3.2 格式化操作...
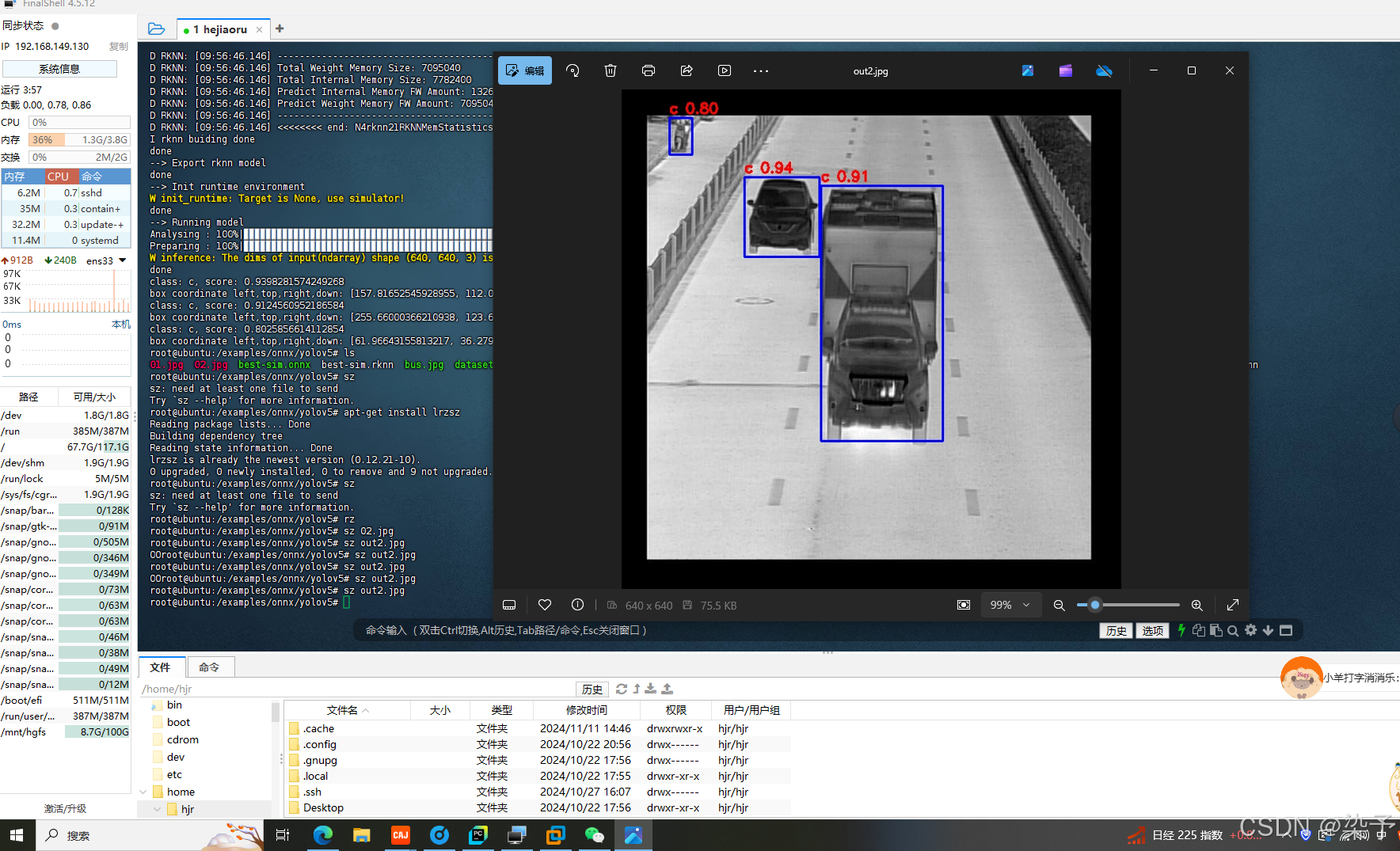
YOLOV5 /onnx模型转换成rknn
上两篇文章讲述了pytorch模型下best.pt转换成onnx模型,以及将onnx进行简化成为best-sim.onnx, 接下来这篇文章讲述如何将onnx模型转换成rknn模型,转换成该模型是为了在rk3568上运行 1.创建share文件夹 文件夹包含以下文件best-sim.onnx,rknn-tookit2-…...
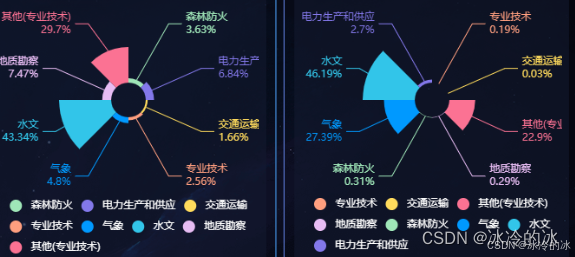
Echarts+VUE饼图的使用(基础使用、多个饼图功能、单组饼图对应颜色使用)
安装:npm install echarts --save 配置:main.js // 引入echarts import * as echarts from echarts Vue.prototype.$echarts echarts一、基础饼图(直接拷贝就能出效果) <div class"big-box" ref"demoEhart"><…...
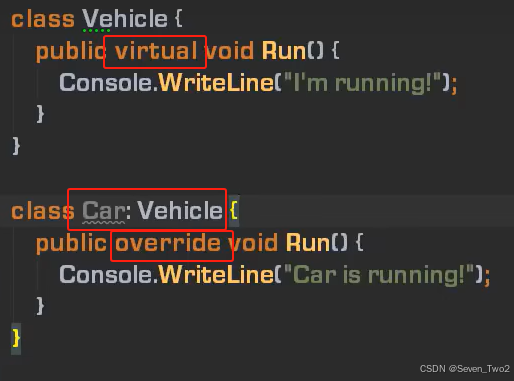
刘铁猛C#入门 026 重写与多态
类的继承 类成员的“横向扩展”(成员越来越多)类成员的“纵向扩展”(行为改变,版本增高)类成员的隐藏(不常用)重写与隐藏的发生条件:函数成员,可见,签名一致 函数成员:方法 、属性可见:父类修饰符是public protected …...

《筑牢安全防线:培养 C++安全编程思维习惯之道》
在当今数字化飞速发展的时代,软件安全的重要性已提升到前所未有的高度。C作为一种广泛应用于系统开发、游戏制作、高性能计算等众多领域的编程语言,其程序的安全性更是关乎重大。培养 C安全编程的思维习惯,不仅是开发者个人能力提升的关键&am…...
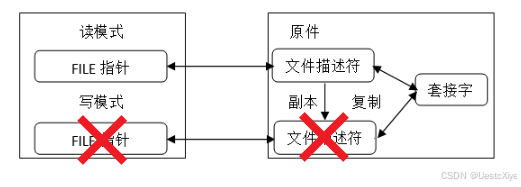
《TCP/IP网络编程》学习笔记 | Chapter 16:关于 I/O 流分离的其他内容
《TCP/IP网络编程》学习笔记 | Chapter 16:关于 I/O 流分离的其他内容 《TCP/IP网络编程》学习笔记 | Chapter 16:关于 I/O 流分离的其他内容分离 I/O 流2 次 I/O 流分离分离「流」的好处「流」分离带来的 EOF 问题 文件描述符的的复制和半关闭终止「流」…...

单片机学习笔记 5. 数码管静态显示
更多单片机学习笔记:单片机学习笔记 1. 点亮一个LED灯单片机学习笔记 2. LED灯闪烁单片机学习笔记 3. LED灯流水灯单片机学习笔记 4. 蜂鸣器滴~滴~滴~ 目录 0、实现的功能 1、Keil工程 1-1 数码管显示原理 1-2 静态与动态显示 1-3 74HC573锁存器的工作原理 1-…...

ValueError: not enough values to unpack (expected 2, got 1) 解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...

java基础知识(常用类)
一、包装类(Wrapper) (1)包装类与基本数据的转换 装箱:基本类型->包装类型 拆箱:包装类型->基本类型 java5以后是自动装箱和拆箱的方式,自动装箱底层调用的是valueOf方法,比如Integer.…...
Selenium+Java(19):使用IDEA的Selenium插件辅助超快速编写Pages
前言 或是惊叹于Selenium对于IDEA的支持已经达到了这样的地步,又或是由于这个好用的小工具的入口就在那里,它已经陪伴了我这么久,而我这么久的时间却都没有发现它。在突然发现这个功能的一瞬间,真的是喜悦感爆棚,于是赶快写下了这篇文章。希望可以帮助到其他同样在做UI自动…...

决策树分类算法【sklearn/决策树分裂指标/鸢尾花分类实战】
决策树分类算法 1. 什么是决策树?2. DecisionTreeClassifier的使用(sklearn)2.1 算例介绍2.2 构建决策树并实现可视化 3. 决策树分裂指标3.1 信息熵(ID3)3.2 信息增益3.3 基尼指数(CART) 4. 代码…...

深入理解 Spring Boot 的 WebApplicationType
1. 前言 在 Spring Boot 应用程序启动过程中,WebApplicationType 是一个重要的概念,它决定了应用程序是以 Web 应用程序的形式运行还是以非 Web 应用程序的形式运行。本文将详细探讨 WebApplicationType 的工作机制及其在实际项目中的应用。 2. 什么是 WebApplicationType?…...

摄影:相机控色
摄影:相机控色 白平衡(White Balance)白平衡的作用: 白平衡的使用环境色温下相机色温下总结 白平衡偏移与包围白平衡包围 影调 白平衡(White Balance) 人眼看到的白色:会自动适应环境光线。 相…...

Python网络爬虫技术及其应用
Python网络爬虫技术及其应用 在当今数字化时代,互联网已经成为信息传播的主要渠道。海量的数据每天都在互联网上产生,这些数据对于企业决策、市场分析、科学研究等有着极其重要的价值。然而,如何高效地收集并利用这些数据成为了一个挑战。Py…...

鸿蒙学习笔记:ArkUI概述
ArkUI是构建分布式应用界面的声明式UI开发框架。组件是界面搭建最小单位,页面是最小调度分隔单位。其有诸多特征,如内置丰富多态UI组件、多样布局、多种动画及绘制能力、交互事件适配多输入设备等,还有平台API通道与两种开发范式。 JS、TS、…...

Selenium 在自动化测试中的应用
在自动化测试中,Selenium是一种非常流行的工具,它允许开发者通过编程的方式与Web浏览器进行交互,模拟用户操作,如点击按钮、填写表单、导航网页等。 1. Selenium 简介 Selenium是一个支持多种浏览器的Web自动化测试工具ÿ…...

python3 Flask应用 使用 Flask-SQLAlchemy操作MySQL数据库
一、环境搭建 下载命令: pip install flask flask-sqlalchemy pymysql 二、创建项目结构 yourProjectFolder/ |—— app.py |—— config.py |—— models.py |__ mydb.py 三、基本使用 3.1 config.py 进行数据库连接配置 import osbasedir os.path.abspat…...

Python学习——猜拳小游戏
import random player int(input(“请输入:剪刀 0,石头 1,布2”)) computer random.randint(0,2)# print(“玩家输入的是%d,电脑输入的是%d” %(player,computer)) 用于测试 if (player 0) and (computer 0) or (player 1) a…...

递归-迭代
24. 两两交换链表中的节点 Leetcode 24 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 递归解法 // 注意:cpp …...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

