拉格朗日乘子(Lagrange Multiplier)是数学分析中用于解决带有约束条件的优化问题的一种重要方法,特别是SVM
拉格朗日乘子(Lagrange Multiplier)是数学分析中用于解决带有约束条件的优化问题的一种重要方法,也称为拉格朗日乘数法。
例如之前博文写的2月7日 SVM&线性回归&逻辑回归在支持向量机(SVM)中,为了找到最佳的分割面(即决策边界),我们确实需要设置目标函数并引入拉格朗日乘子。
1 以下是对拉格朗日乘子的详细解释:
一、定义与基本概念
拉格朗日乘子法主要用于寻找在给定约束条件下,能够最大化或最小化一个函数的解。这里的约束条件通常以一个或多个等式的形式给出。
二、核心思想
拉格朗日乘子法的核心思想是将约束条件引入到目标函数中,通过构建一个新的函数(称为拉格朗日函数),从而将带有约束的优化问题转换为无约束的优化问题。这个新的函数包含了原目标函数和约束条件的线性组合,其中引入了一个新的变量,即拉格朗日乘子,它表示约束条件对目标函数的影响。
三、构建拉格朗日函数
对于目标函数f(x)和约束条件g(x)=0(其中x为变量向量),我们构造拉格朗日函数L(x,λ)=f(x)-λg(x)。其中,λ为拉格朗日乘子,g(x)为约束条件。
四、求解步骤
- 构造拉格朗日函数:根据目标函数和约束条件,构造出拉格朗日函数。
- 求偏导数:对拉格朗日函数分别关于变量向量x和拉格朗日乘子λ求偏导数,并设这些偏导数为0,形成一组方程。
- 解方程组:解这组方程,找到变量向量x和拉格朗日乘子λ的解。
- 验证解:将找到的解代入原目标函数和约束条件,验证是否满足极值条件和约束条件。
五、几何解释
从几何角度来看,拉格朗日乘子法的原理是在约束条件所表示的曲面上,目标函数的梯度和约束条件的梯度是共线的(平行的)。也就是说,目标函数在满足约束的点处,其梯度是约束条件的线性组合。如果我们可以找到拉格朗日乘子λ,使得目标函数和约束条件的梯度是平行的,那么这个点就是满足约束条件的最优点。
六、应用实例
拉格朗日乘子法在多个领域都有广泛应用,如经济学中的效用最大化问题、物理学中的力学问题、机器学习中的支持向量机(SVM)等。
七、注意事项
- 拉格朗日乘子法通常适用于等式约束的优化问题。对于不等式约束的优化问题,需要使用其他方法,如卡罗需-库恩-塔克(KKT)条件等。
- 在应用拉格朗日乘子法时,需要注意约束条件的可行性和目标函数的可微性。
综上所述,拉格朗日乘子法是解决带有约束条件的优化问题的一种有效方法,它通过构建拉格朗日函数将约束条件和目标函数结合起来,从而转换成无约束的优化问题。这种方法在数学优化、经济学、物理学和机器学习等领域都有广泛应用。
2 在支持向量机(SVM)中详细的步骤和解释:
2.1. 设置目标函数和约束条件
SVM 的目标是找到一个超平面(在二维空间中为直线,三维空间中为平面,以此类推),该超平面能够将数据点尽可能好地分开。为了量化“尽可能好地分开”,我们引入了间隔(margin)的概念。间隔是指超平面到其最近的数据点(即支持向量)的距离。SVM 的目标是最大化这个间隔。
目标函数(也称为优化问题)通常表示为:
max w , b 2 ∥ w ∥ \max_{\mathbf{w}, b} \frac{2}{\|\mathbf{w}\|} maxw,b∥w∥2
其中, w \mathbf{w} w 是超平面的法向量, b b b 是截距。这个表达式是在最大化间隔(因为间隔与 1 ∥ w ∥ \frac{1}{\|\mathbf{w}\|} ∥w∥1 成正比,所以我们最大化 2 ∥ w ∥ \frac{2}{\|\mathbf{w}\|} ∥w∥2 或等价地最小化 1 2 ∥ w ∥ 2 \frac{1}{2}\|\mathbf{w}\|^2 21∥w∥2)。
约束条件是:
y i ( w ⋅ x i + b ) ≥ 1 , ∀ i y_i(\mathbf{w} \cdot \mathbf{x}_i + b) \geq 1, \quad \forall i yi(w⋅xi+b)≥1,∀i
其中, y i y_i yi 是数据点 x i \mathbf{x}_i xi 的标签(正类或负类), w ⋅ x i \mathbf{w} \cdot \mathbf{x}_i w⋅xi 是向量 w \mathbf{w} w 和 x i \mathbf{x}_i xi 的点积。
2. 引入拉格朗日乘子
为了求解这个带有约束条件的优化问题,我们引入拉格朗日乘子 α i ≥ 0 \alpha_i \geq 0 αi≥0,并构造拉格朗日函数:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 N α i [ y i ( w ⋅ x i + b ) − 1 ] L(\mathbf{w}, b, \alpha) = \frac{1}{2}\|\mathbf{w}\|^2 - \sum_{i=1}^N \alpha_i [y_i(\mathbf{w} \cdot \mathbf{x}_i + b) - 1] L(w,b,α)=21∥w∥2−∑i=1Nαi[yi(w⋅xi+b)−1]
3. 求解拉格朗日函数
接下来,我们对拉格朗日函数关于 w \mathbf{w} w 和 b b b 求偏导数,并设它们为0,以找到极值点。这会导致以下两个条件:
∂ L ∂ w = 0 ⇒ w = ∑ i = 1 N α i y i x i \frac{\partial L}{\partial \mathbf{w}} = 0 \Rightarrow \mathbf{w} = \sum_{i=1}^N \alpha_i y_i \mathbf{x}_i ∂w∂L=0⇒w=∑i=1Nαiyixi
∂ L ∂ b = 0 ⇒ ∑ i = 1 N α i y i = 0 \frac{\partial L}{\partial b} = 0 \Rightarrow \sum_{i=1}^N \alpha_i y_i = 0 ∂b∂L=0⇒∑i=1Nαiyi=0
将这两个条件代入拉格朗日函数,我们得到一个只包含 α i \alpha_i αi 的函数(称为拉格朗日对偶函数)。
4. 求解对偶问题
现在,我们需要最大化拉格朗日对偶函数,同时满足约束条件 α i ≥ 0 \alpha_i \geq 0 αi≥0 和 ∑ i = 1 N α i y i = 0 \sum_{i=1}^N \alpha_i y_i = 0 ∑i=1Nαiyi=0。这通常通过求解一个二次规划(QP)问题来完成。
5. 推导出分割面
一旦我们找到了最优的 α i \alpha_i αi,我们就可以使用它们来找到最优的 w \mathbf{w} w 和 b b b。然后,分割面(或决策边界)可以表示为:
w ⋅ x + b = 0 \mathbf{w} \cdot \mathbf{x} + b = 0 w⋅x+b=0
其中, w \mathbf{w} w 是由支持向量的线性组合给出的,而 b b b 可以通过任何支持向量来计算(使用 y i ( w ⋅ x i + b ) = 1 y_i(\mathbf{w} \cdot \mathbf{x}_i + b) = 1 yi(w⋅xi+b)=1 的条件)。
总结
通过引入拉格朗日乘子并求解对偶问题,SVM 能够找到最大化间隔的分割面。这个分割面是由支持向量决定的,即那些位于间隔边界上的数据点。
相关文章:
是数学分析中用于解决带有约束条件的优化问题的一种重要方法,特别是SVM)
拉格朗日乘子(Lagrange Multiplier)是数学分析中用于解决带有约束条件的优化问题的一种重要方法,特别是SVM
拉格朗日乘子(Lagrange Multiplier)是数学分析中用于解决带有约束条件的优化问题的一种重要方法,也称为拉格朗日乘数法。 例如之前博文写的2月7日 SVM&线性回归&逻辑回归在支持向量机(SVM)中,为了…...

鸿蒙征文|鸿蒙心路旅程:始于杭研所集训营,升华于横店
始于杭研所 在2024年7月,我踏上了一段全新的旅程,前往风景如画的杭州,参加华为杭研所举办的鲲鹏&昇腾集训营。这是一个专门为开发者设计的培训项目,中途深入学习HarmonyOS相关技术。对于我这样一个对技术充满热情的学生来说&…...

c语言数据结构与算法--简单实现线性表(顺序表+链表)的插入与删除
老规矩,点赞评论收藏关注!!! 目录 线性表 其特点是: 算法实现: 运行结果展示 链表 插入元素: 删除元素: 算法实现 运行结果 线性表是由n个数据元素组成的有限序列ÿ…...
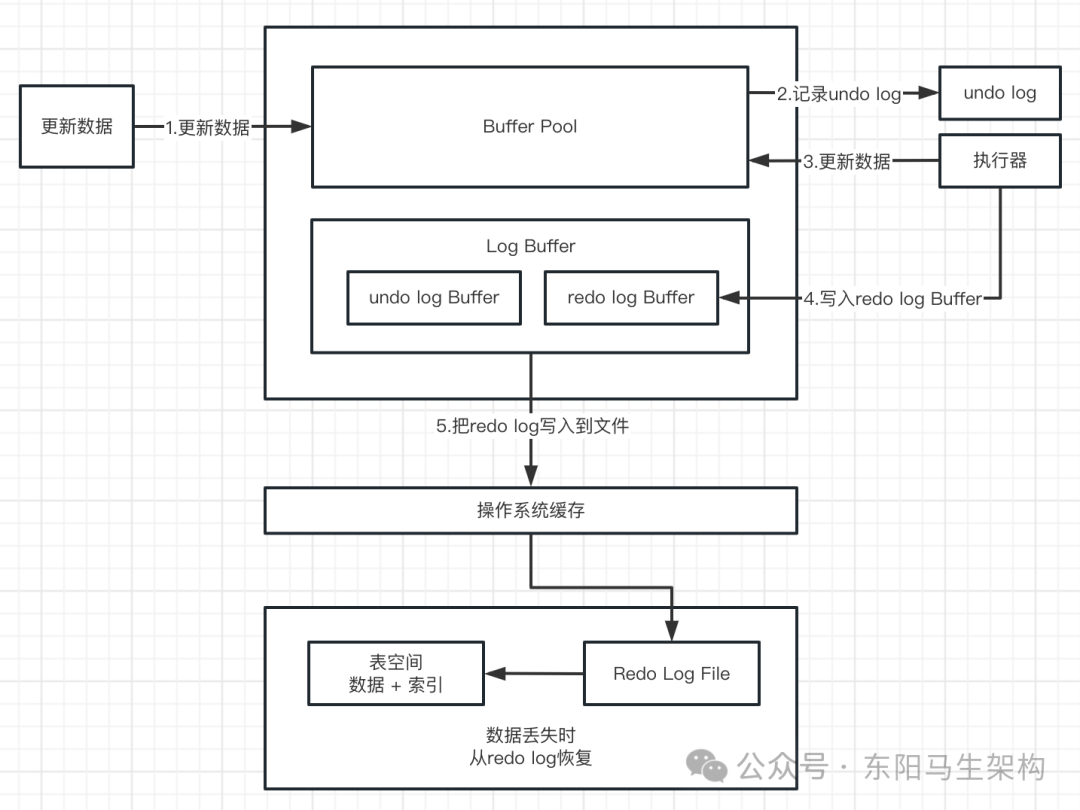
MySQL底层概述—1.InnoDB内存结构
大纲 1.InnoDB引擎架构 2.Buffer Pool 3.Page管理机制之Page页分类 4.Page管理机制之Page页管理 5.Change Buffer 6.Log Buffer 1.InnoDB引擎架构 (1)InnoDB引擎架构图 (2)InnoDB内存结构 (1)InnoDB引擎架构图 下面是InnoDB引擎架构图,主要分为内存结构和磁…...
计算两个日期天数之差)
MySQL:DATEDIFF()计算两个日期天数之差
题目需求: 计算出比前一天温度要高的日期。 select a.id from weather a, weather b where a.temperature > b.temperature and datediff(a.recordDate, b.recordDate) 1; DATEDIFF(date1, date2)函数用于计算两个日期之间的天数差。函数返回date1和date2之…...

Linux 编译Ubuntu24内核
参考来源: 编译并更新内核:https://www.cnblogs.com/smlile-you-me/p/18248433 编译报错–sub-make: https://forum.linuxfoundation.org/discussion/865005/facing-error-in-building-the-kernel 1.下载源码,执行如下命令,会在/usr/src下多…...

Android系统中init进程、zygote进程和SystemServer进程简单学习总结
Android系统中,init、zygote和SystemServer进程是系统启动和运行的关键进程,它们之间有着密切的关系,本文针对这三个进程的学习做一个简单汇总,方便后续查询。 1、init进程 Android用户空间执行的第一个程序就是它,可…...

Flask 基于wsgi源码启动流程
1. 点击 __call__ 进入到源码 2. 找到 __call__ 方法 return 执行的是 wsgi方法 3. 点击 wsgi 方法 进到 wsgi return 执行的是 response 方法 4. 点击response 方法 进到 full_dispatch_request 5. full_dispatch_request 执行finalize_request 方法 6. finalize_request …...

leetcode代码 50道答案
简单难度:两数之和 def twoSum(nums, target): for i in range(len(nums)): for j in range(i 1, len(nums)): if nums[i] nums[j] target: return [i, j] return [] 简单难度:有效的括号 def isVa…...

Centos-stream 9,10 add repo
Centos-stream repo前言 Centos-stream 9,10更换在线阿里云创建一键更换repo 自动化脚本 华为centos-stream 源 , 阿里云centos-stream 源 华为epel 源 , 阿里云epel 源vim /centos9_10_repo.sh #!/bin/bash # -*- coding: utf-8 -*- # Author: make.h...

【隐私计算大模型】联邦深度学习之拆分学习Split learning原理及安全风险、应对措施以及在大模型联合训练中的应用案例
Tips:在两方场景下,设计的安全算法,如果存在信息不对等性,那么信息获得更多的一方可以有概率对另一方实施安全性攻击。 1. 拆分学习原理 本文介绍了一种适用于隐私计算场景的深度学习实现方案——拆分学习,又称分割…...

DataWhale—PumpkinBook(TASK05决策树)
课程开源地址及相关视频链接:(当然这里也希望大家支持一下正版西瓜书和南瓜书图书,支持文睿、秦州等等致力于开源生态建设的大佬✿✿ヽ(▽)ノ✿) Datawhale-学用 AI,从此开始 【吃瓜教程】《机器学习公式详解》(南瓜…...

elasticsearch7.10.2集群部署带认证
安装elasticsearch rpm包安装 下载地址 https://mirrors.aliyun.com/elasticstack/7.x/yum/7.10.2/ 生成证书 #1.生成CA证书 # 生成CA证书,执行命令后,系统还会提示你输入密码,可以直接留空 cd /usr/share/elasticsearch/bin ./elasticsearch-certutil ca#会在/usr/share/el…...

Java基础-I/O流
(创作不易,感谢有你,你的支持,就是我前行的最大动力,如果看完对你有帮助,请留下您的足迹) 目录 字节流 定义 说明 InputStream与OutputStream示意图 说明 InputStream的常用方法 说明 OutputStrea…...
全面解析多种mfc140u.dll丢失的解决方法,五种方法详细解决
当你满心期待地打开某个常用软件,却突然弹出一个错误框,提示“mfc140u.dll丢失”,那一刻,你的好心情可能瞬间消失。这种情况在很多电脑用户的使用过程中都可能出现。无论是游戏玩家还是办公族,面对这个问题都可能不知所…...

详细探索xinput1_3.dll:功能、问题与xinput1_3.dll丢失的解决方案
本文旨在深入探讨xinput1_3.dll这一动态链接库文件。首先介绍其在计算机系统中的功能和作用,特别是在游戏和输入设备交互方面的重要性。然后分析在使用过程中可能出现的诸如文件丢失、版本不兼容等问题,并提出相应的解决方案,包括重新安装相关…...
)
InfluxDB时序数据库笔记(一)
InfluxDB笔记一汇总 1、时间序列数据库概述2、时间序列数据库特点3、时间序列数据库应用场景4、InfluxDB数据生命周期5、InfluxDB历史数据需要另外归档吗?6、InfluxDB历史数据如何归档?7、太麻烦了,允许的话选择设施完备的InfluxDB云产品吧8、…...

Spring Boot 3.x + OAuth 2.0:构建认证授权服务与资源服务器
Spring Boot 3.x OAuth 2.0:构建认证授权服务与资源服务器 前言 随着Spring Boot 3的发布,我们迎来了许多新特性和改进,其中包括对Spring Security和OAuth 2.0的更好支持。本文将详细介绍如何在Spring Boot 3.x版本中集成OAuth 2.0…...

2024年09月CCF-GESP编程能力等级认证Scratch图形化编程二级真题解析
本文收录于《Scratch等级认证CCF-GESP图形化真题解析》专栏,专栏总目录:点这里,订阅后可阅读专栏内所有文章。 一、单选题(共 10 题,每题 3 分,共 30 分) 第 1 题 据有关资料,山东大学于 1972 年研制成功 DJL-1 计算机,并于 1973 年投入运行,其综合性能居当时全国第…...
)
Linux 正则表达式(basic and extened)
正则表达式(Regular Expressions),整理自: https://pubs.opengroup.org/onlinepubs/9699919799/basedefs/V1_chap09.html gred sed 定义 Regular Expressions (REs) provide a mechanism to select specific strings from a set of character strings.…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...
