《线性代数的本质》
之前收藏的一门课,刚好期末复习,顺便看一看哈哈
课程链接:【线性代数的本质】合集-转载于3Blue1Brown官方双语】
向量究竟是什么
线性代数中最基础、最根源的组成部分就是向量,需要先明白什么是向量
不同专业对向量的看法
- 物理专业:长度和方向
- 计算机专业:有序的数字列表
- 数学专业:加法和数乘
思考向量的特定方式
几何方面:向量是空间中的箭头,线性代数中,一般选择原点作为起点。可以和数字列表结合起来,为了把点(-2, 3)和向量(-2, 3)区分开来,一般将向量竖着写,用方括号括起来,这样每一对数和向量就一一对应了,三维空间类似。


向量加法
将w向量从原点沿着v向量的方向向上平移,如下图所示,可以得到两向量的和向量。视频中提到,将向量看作一种运动,就是想空间中某一方向移动一段距离,例如,先沿着v运动,再沿着w运动,和你沿着他们的和向量运动是一样的。


向量数乘
将一个数字乘以一个向量,相当于对这个向量进行缩放,这个数字也称为“标量”,主要作用就是对向量进行缩放

线性组合:张成的空间与基
二维平面,有两个特殊的向量,”基向量“,每当我们使用数字描述向量,它都依赖于我们正在使用的基。两个向量全部线性组合构成的向量称为**“张成的空间”**

当考虑一个向量的时候,将其看作箭头,当考虑多个向量的时候,就将每个向量看作一个点,在三维空间中取两个指向不同方向的向量,对红和蓝两标量进行缩放相加,可以得到绿色,逐渐改变标量,可以得到一个过坐标原点的平面,此时随机加入一个向量,该向量不在之前两向量张成的空间内,由于他们指向不同方向,所以可以得到所有的三维向量,可以理解为第三个向量将前两个向量张成的平面来回移动,从而扫过整个空间。



- 线性相关:一个向量可以表示为其他向量的线性组合
- 线性无关:如果所有的向量都给张成的空间增加了新的维度,则被称为线性无关
基的严格定义:向量空间的一组基是张成该空间的一个线性无关向量集。
矩阵和线性变换
我感觉这个up通过可视化进行讲述,先举出特定的例子帮助理解,然后再归一到一般情况进行全面总结。这里,线性变化抓住最本质的东西,确定基向量,将矩阵看作空间的变换。
线性变换的理解:
函数,根据输入,得到输出的过程,而变换,则暗示以特定方式来可视化这一输入输出的关系。
空间中的变换的多样的,线性代数的变换更容易理解,怎么理解线性呢?需要满足两个条件,一个是变换之后直线依然是直线,二是原点必须保持固定。保证了网格线平行且等距分布,并且保持原点不动。将矩阵看作空间变换,这个思想对后续章节都有作用
如何用数值描述线性变换,给定一个向量坐标,可以得到一个变换之后的向量坐标?实际只需要记住基向量变换之后的位置,由此可见,一个线性变换只要四个元素就可以确定,变换后i帽的两个坐标和变换后j帽的两个坐标。



矩阵乘法与线性变换复合的联系
回顾之前的内容,线性变换是将向量作为输入和输出的函数,可以将线性变换看作是对空间的挤压,他保持网格线平行且等距分布,并且保持原点不变,核心在于抓住基向量的变化,因为其他向量都可以通过基向量表示。
矩阵乘法的意义就是,就是两个变换的相继作用
就像求解函数的时候,总是从里到外,从右向左进行求解,矩阵运算也是一样的,我们先进行旋转操作,再进行剪切操作,也是从右向左进行操作。



我们看一下如何进行运算,首先看M1的第一列,这是i向量第一变换后的结果,然后计算其在M2作用下的结果,得到符合运算的第一列;同理j帽的变化类似


相继变换的一些性质:
由下面两图可以看出,两次作用的先后顺序对结果是有影响的


但是线性变换满足结合律,因为并没有改变作用的顺序,还是从左到右进行变换操作,因此矩阵乘法具有结合性。
相关文章:

《线性代数的本质》
之前收藏的一门课,刚好期末复习,顺便看一看哈哈 课程链接:【线性代数的本质】合集-转载于3Blue1Brown官方双语】 向量究竟是什么 线性代数中最基础、最根源的组成部分就是向量,需要先明白什么是向量 不同专业对向量的看法 物理专…...

Gbase8s 允许内置用户创建用户以及创建只读权限用户以及利用角色管理普通用户权限
Gbase8s 允许内置用户创建用户以及创建只读权限用户以及利用角色管理普通用户权限 普通安装实例创建数据库以后,DBA权限只有gbasedbt用户。gbasdbt可以创建普通用户,并且给普通用户赋予库及权限或者表级权限。 但是gbasedbt用户口令和操作系统相关,所以想在不提供gbasedbt的…...

24/11/25 视觉笔记 深度传感器和手势识别
本章的目的是开发一个应用程序,使用深度传感器的输出实时检测和跟踪简单的手势。该应用程序将分析每个已捕捉的帧。并执行以下任务。 手部区域分割:通过分析Kinect传感器的深度图输出,在每一帧中提取用户的手部区域,这是通过阈值…...

迄今为止的排序算法总结
迄今为止的排序算法总结 7.10 迄今为止的排序算法总结复杂度和稳定性时间复杂度测试程序sortAlgorithm.hsortAlgorithm.cpptest.cpp 时间复杂度测试结果 7.10 迄今为止的排序算法总结 复杂度和稳定性 排序算法平均情况最好情况最坏情况稳定性空间复杂度选择排序O(n^2)O(n^2)O…...

HTML和CSS 表单、表格练习
HTML和CSS 表格练习 <!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>HTML表格练习</title>…...

H5流媒体播放器EasyPlayer.js网页直播/点播播放器如果H.265视频在播放器上播放不流畅,可以考虑的解决方案
随着流媒体技术的迅速发展,H5流媒体播放器已成为现代网络视频播放的重要工具。其中,EasyPlayer.js网页直播/点播播放器作为一款功能强大的H5播放器,凭借其全面的协议支持、多种解码方式以及跨平台兼容性,赢得了广泛的关注和应用。…...

Http 转 https 中 Nginx 的详细配置过程
摘要 本节将简要介绍从 HTTP 到 HTTPS 的配置过程,并完整展示 Nginx 的相关配置信息。 经过两天断断续续的调试,终于将 http 变成 https 了。现在说说这个安装 ssl 证书的过程。 服务器是在某云上。这个过程大致分为三个步骤:申请 ssl 证书、…...
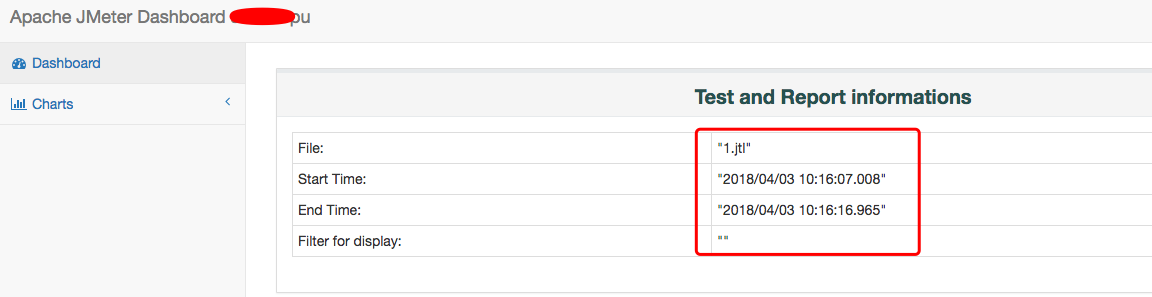
【测试工具JMeter篇】JMeter性能测试入门级教程(二)出炉,测试君请各位收藏了!!!
上篇文章:CSDN 我们介绍了JMeter的一些原理介绍,以及安装配置和启动流程,本文我们就来讲讲JMeter如何使用。 一、JMeter目录结构组成 1. 根目录 Jmeter安装包解压后的根目录如下图: 1.1 backups目录:脚本备份目录&am…...

Otter 安装流程
优质博文:IT-BLOG-CN 一、背景 随着公司的发展,订单库的数据目前已达到千万级别,需要进行分表分库,就需要对数据进行迁移,我们使用了otter,这里简单整理下,otter 的安装过程,希望对…...

一文学会Golang里拼接字符串的6种方式(性能对比)
g o l a n g golang golang的 s t r i n g string string类型是不可修改的,对于拼接字符串来说,本质上还是创建一个新的对象将数据放进去。主要有以下几种拼接方式 拼接方式介绍 1.使用 s t r i n g string string自带的运算符 ans ans s2. 使用…...

【笔记】Linux下编译Python3.10.15为动态库同时正确处理OpenSSL3依赖
之前自己第一次编译Python后发现pip会提示无法使用SSL,后来了解到是自己编译时没有配置OpenSSL。这个过程有点曲折,里面有一个坑,怕忘记于是写博客记录一下。 首先是下载OpenSSL,Python3.10.15支持此时最新版的OpenSSL 3.4.0&…...

Go语言获取客户端真实IP
在一些需求中,服务器需要记录客户端的ip地址,要获取ip地址,则需要有http.Request的对象参数传入,以下代码直接放在util中使用。 文件名:ip_utils.go package utilsimport ("context""github.com/spf1…...
)
大模型论文速递(11.23-11.25)
BlueLM-V3B 关键词:动态分辨率,图像放大,适应性网格化方法 研究问题:如何改进现有的动态分辨率匹配方法以减少在模型训练和部署中的计算复杂度? 方法: 分析现有动态分辨率匹配算法(如LLaVA-…...
)
维护在线重做日志(二)
迁移和重命名 可以使用操作系统命令重新定位重做日志,然后使用ALTER DATABASE语句使数据库知道它们的新名称(位置)。这个过程是必要的,例如,如果当前用于一些重做日志文件的磁盘将被删除,或者如果数据文件…...

.net core MVC入门(一)
文章目录 项目地址一、环境配置1.1 安装EF core需要包1.2 配置数据库连接二、使用EF创建表2.1 整体流程梳理2.1 建表详细流程三、添加第一个视图3.1整体流程梳理3.1 添加视图,并显示在web里四、使用EF增加Catogory数据,并且读取数据到页面4.1整体流程梳理4.2 实现五、增加Cat…...

802.11协议
802.11协议是由美国电气和电子工程师协会(IEEE)制定的无线局域网(WLAN)标准。以下是关于802.11协议的详细介绍: 一、定义与背景 定义:IEEE802.11是美国电机电子工程师协会(IEEE)为…...

【Linux】线程ID与互斥、同步(锁、条件变量)
作者主页: 作者主页 本篇博客专栏:Linux 创作时间 :2024年11月24日 线程ID及进程地址空间布局 先看一下这段代码: 运行一下: 运行这个代码之后,我们看到的这个很大的数字就是线程id,然后…...

Android 13 编译Android Studio版本的Launcher3
Android 13 Aosp源码 源码版本 Android Studio版本 Launcher3QuickStepLib (主要代码) Launcher3ResLib(主要资源) Launcher3IconLoaderLib(图片加载,冲突资源单独新建) 需要值得注意的是: SystemUISharedLib.jar 有kotlin和java下的,在 Lau…...

burp功能介绍
声明! 学习视频来自B站up主 **泷羽sec** 有兴趣的师傅可以关注一下,如涉及侵权马上删除文章,笔记只是方便各位师傅的学习和探讨,文章所提到的网站以及内容,只做学习交流,其他均与本人以及泷羽sec团队无关&a…...

Android12 的 Vold梳理
1.代码位置 system/vold/ 路径下,查看bp文件,发现是编译system/vold/main.cpp编译生成可执行文件vold 2.app侧调用代码流程 2.1 整体框架 #mermaid-svg-lqO8phN62rKNW407 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
