【leetcode】动态规划
31. 873. 最长的斐波那契子序列的长度
题目:
如果序列
X_1, X_2, ..., X_n满足下列条件,就说它是 斐波那契式 的:
n >= 3- 对于所有
i + 2 <= n,都有X_i + X_{i+1} = X_{i+2}给定一个严格递增的正整数数组形成序列 arr ,找到 arr 中最长的斐波那契式的子序列的长度。如果一个不存在,返回 0 。
(回想一下,子序列是从原序列 arr 中派生出来的,它从 arr 中删掉任意数量的元素(也可以不删),而不改变其余元素的顺序。例如,
[3, 5, 8]是[3, 4, 5, 6, 7, 8]的一个子序列)
题目链接
873. 最长的斐波那契子序列的长度 - 力扣(LeetCode)
画图分析
代码
class Solution { public:int lenLongestFibSubseq(vector<int>& arr) {int n = arr.size();vector<vector<int>>dp(n,vector<int>(n,0));map<int,int>hash;hash.insert({arr[0],0});int len = 0;for(int j = 2;j < n;j++){hash.insert({arr[j - 1],j - 1});for(int i = j - 1;i >= 1;i--){int x = arr[j] - arr[i];if(hash.count(x) && hash[x] < i){dp[i][j] = max(dp[i][j],dp[hash[x]][i] + 1);len = max(len,dp[i][j]);}}}if(len == 0){return 0;}return len + 2;} };
32. 1027. 最长等差数列
题目:
给你一个整数数组
nums,返回nums中最长等差子序列的长度。回想一下,
nums的子序列是一个列表nums[i1], nums[i2], ..., nums[ik],且0 <= i1 < i2 < ... < ik <= nums.length - 1。并且如果seq[i+1] - seq[i](0 <= i < seq.length - 1) 的值都相同,那么序列seq是等差的。
题目链接
1027. 最长等差数列 - 力扣(LeetCode)
文字分析
主要解题思路参考 873.最长的斐波那契子序列的长度
同样的我们可以通过两个元素,反推前面一个数
注意:
1. 这道题目没有规定一个数不能重复出现,所以判断前一个数是否存在,得到的下标有多个,要得到最大的子序列,下标应该最近的那个(实现这一点,hash表可以采取覆盖式的更新下标)
2. 这里的最长长度至少是2,任意两个数也构成定差子序列
代码
class Solution { public:int longestArithSeqLength(vector<int>& nums) {map<int,int> hash;hash[nums[0]] = 0;int n = nums.size();int Max = 2;vector<vector<int>> dp(n,vector<int>(n,2));for(int i = 1;i < n;i++){for(int j = i + 1;j < n;j++){int a = 2 * nums[i] - nums[j];if(hash.count(a)){dp[i][j] = dp[hash[a]][i] + 1;}Max = max(Max,dp[i][j]);}hash[nums[i]] = i; //更新下标}return Max;} };
33. 446. 等差数列划分2 -- 子序列
题目:
给你一个整数数组
nums,返回nums中所有 等差子序列 的数目。如果一个序列中 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该序列为等差序列。
- 例如,
[1, 3, 5, 7, 9]、[7, 7, 7, 7]和[3, -1, -5, -9]都是等差序列。- 再例如,
[1, 1, 2, 5, 7]不是等差序列。数组中的子序列是从数组中删除一些元素(也可能不删除)得到的一个序列。
- 例如,
[2,5,10]是[1,2,1,2,4,1,5,10]的一个子序列。题目数据保证答案是一个 32-bit 整数。
题目链接
446. 等差数列划分 II - 子序列 - 力扣(LeetCode)
文字分析
这道题和 1027.最长等差数列 相似,唯一最大的不同是:
由题目的示例2可知,子序列可以重复多算
注意:
这道题算出来的一些数很可能会越界,得用 long long 存储
代码
class Solution { public:int numberOfArithmeticSlices(vector<int>& nums) {unordered_map<long long, vector<int>> hash;int n = nums.size();vector<vector<long long>>dp(n, vector<long long>(n, 0)); //模拟哈希桶int len = 0;hash[nums[0]].push_back(0);for (int j = 2; j < n; j++){for (int i = j - 1; i >= 1; i--){long long x = (long long)2 * nums[i] - nums[j]; //不做强转,数据会溢出if (hash.count(x)){for (int e : hash[x]){if (e < i){dp[i][j] += (dp[e][i] + 1);}}len += dp[i][j];}}hash[nums[j - 1]].push_back(j - 1);}return len; } };

相关文章:

【leetcode】动态规划
31. 873. 最长的斐波那契子序列的长度 题目: 如果序列 X_1, X_2, ..., X_n 满足下列条件,就说它是 斐波那契式 的: n > 3对于所有 i 2 < n,都有 X_i X_{i1} X_{i2} 给定一个严格递增的正整数数组形成序列 arr ࿰…...
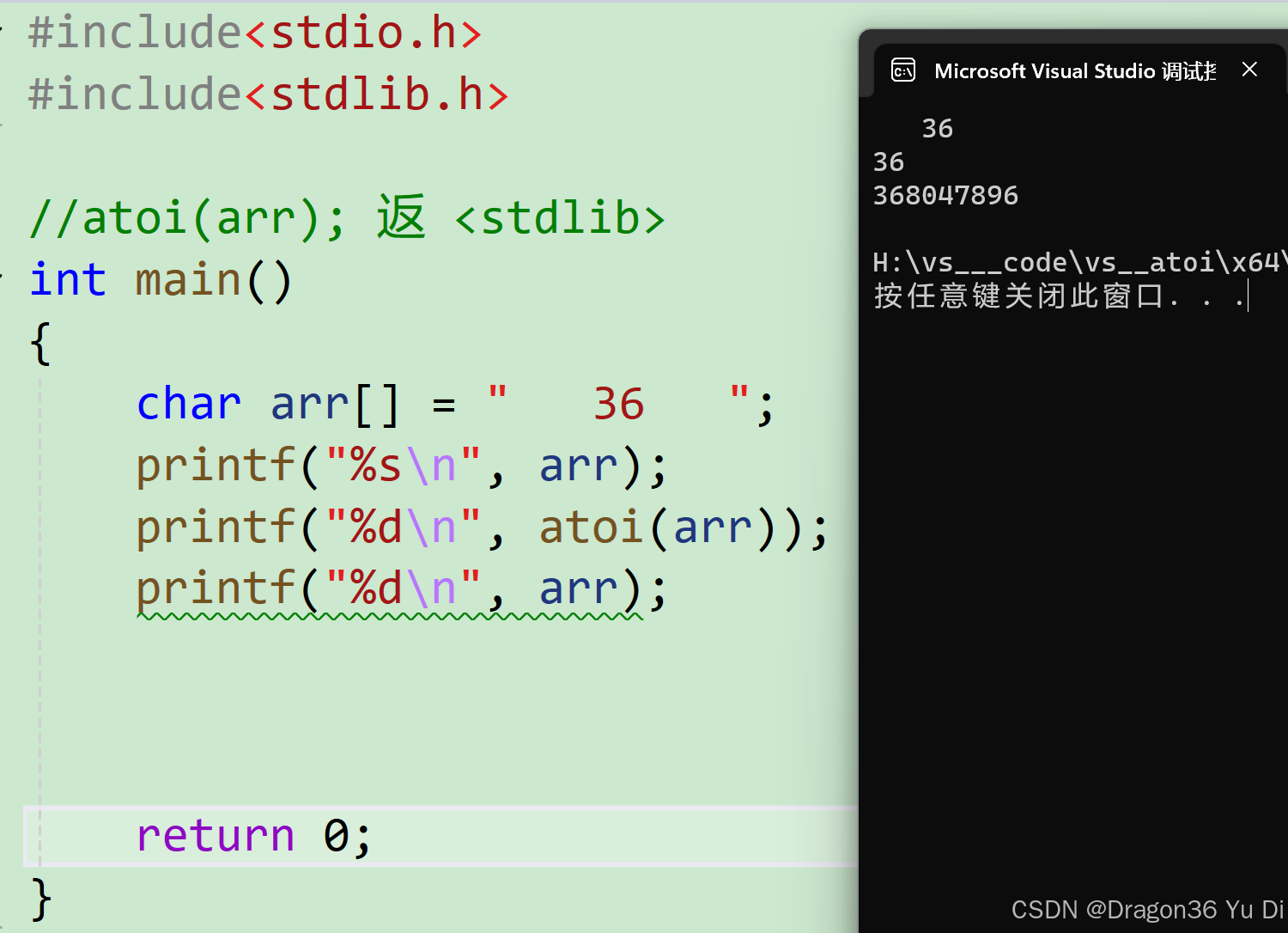
介绍一下atoi(arr);(c基础)
hi , I am 36 适合对象c语言初学者 atoi(arr);是返回整数(int型),整数是arr数组中字符中数字 格式 #include<stdio.h> atoi(arr); 返回值arr数组中的数字 未改变arr数组 #include<stdlib.h>//atoi(arr); 返 <stdlib> int main(…...

docker入门学习笔记
docker的定义 docker是一个用于构建、运行、传送 应用程序的平台。 为什么要使用docker ? 在开发测试库环境中测试成功后,打包成集装箱,到生产环境也是能够成功的。而传统的安装方式不仅繁琐,并且在测试环境安装后,到…...

使用Python和Pybind11调用C++程序(CMake编译)
目录 一、前言二、安装 pybind11三、编写C示例代码四、结合Pybind11和CMake编译C工程五、Python调用动态库六、参考 一、前言 跨语言调用能对不同计算机语言进行互补,本博客主要介绍如何实现Python调用C语言编写的函数。 实验环境: Linux gnuPython3.10…...
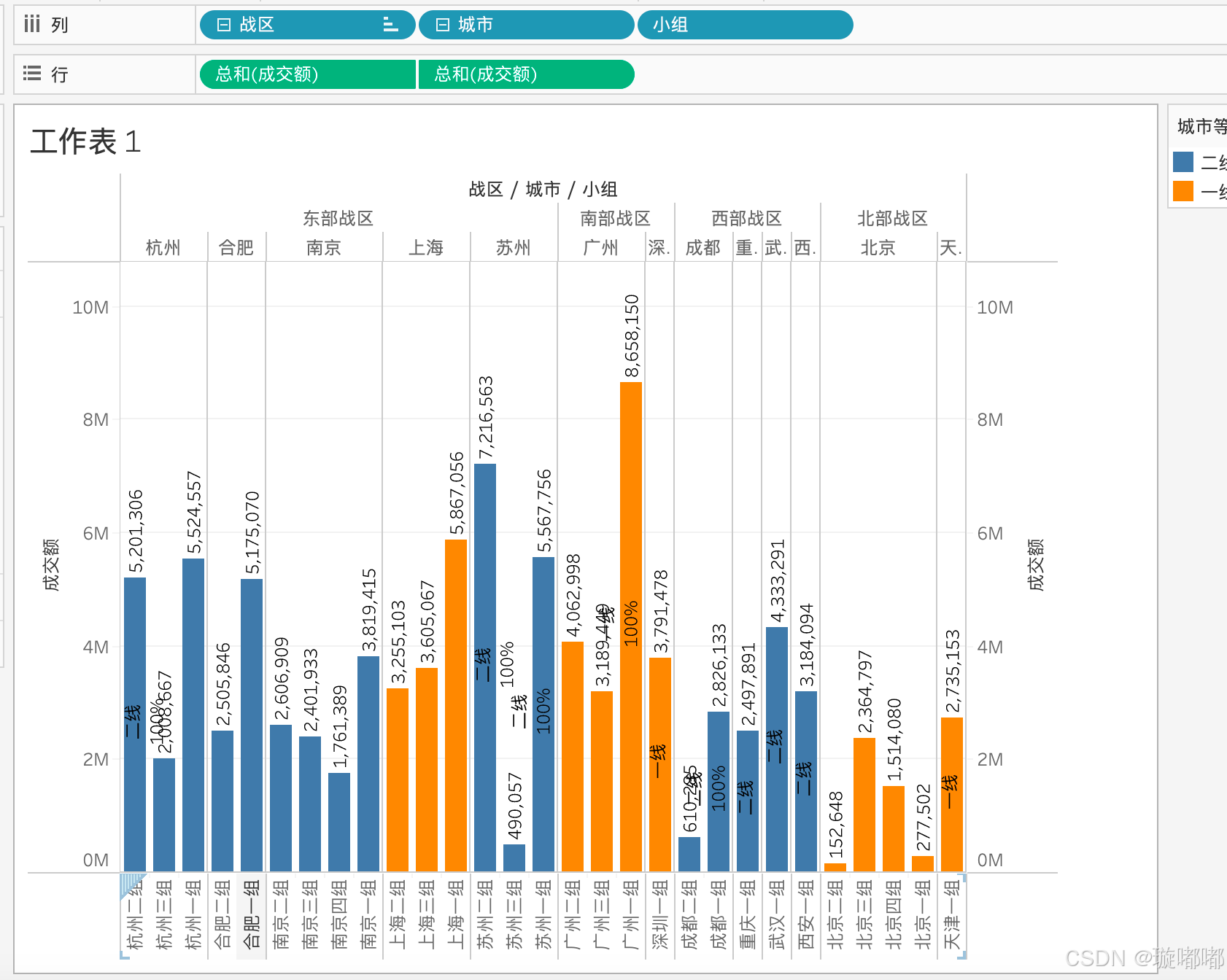
tableau-制作30个图表
制作条形图 步骤: 1、横轴是数值,对应了某一个度量值,纵轴是一个标签 战区的成交额,条形图横轴是战区,纵轴是成交额 下钻条形图 1、增加业务架构-战区右键点击,分层结构,增加分层结构 调整业务架构,将战区,城市,小组移动到业务架构下方 此时的条形图上方有➕号展开后…...

2024APMCM亚太杯数学建模C题【宠物行业】原创论文分享
大家好呀,从发布赛题一直到现在,总算完成了2024 年APMCM亚太地区大学生数学建模竞赛C题的成品论文。 给大家看一下目录吧: 目录 摘 要: 10 一、问题重述 14 二.问题分析 15 2.1问题一 15 2.2问题二 15 2.3问题三…...
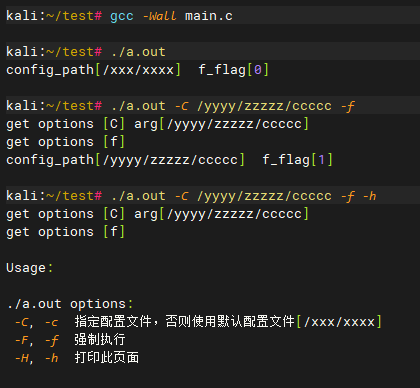
C语言解析命令行参数
原文地址:C语言解析命令行参数 – 无敌牛 欢迎参观我的个人博客:无敌牛 – 技术/著作/典籍/分享等 C语言有一个 getopt 函数,可以对命令行进行解析,下面给出一个示例,用的时候可以直接copy过去修改,很方便…...
推荐一款龙迅HDMI2.0转LVDS芯片 LT6211UX LT6211UXC
龙迅的HDMI2.0转LVDS芯片LT6211UX和LT6211UXC是两款高性能的转换器芯片,它们在功能和应用上有所差异,同时也存在一些共同点。以下是对这两款芯片的详细比较和分析: 一、LT6211UX 主要特性: HDMI2.0至LVDS和MIPI转换器。HDMI2.0输…...
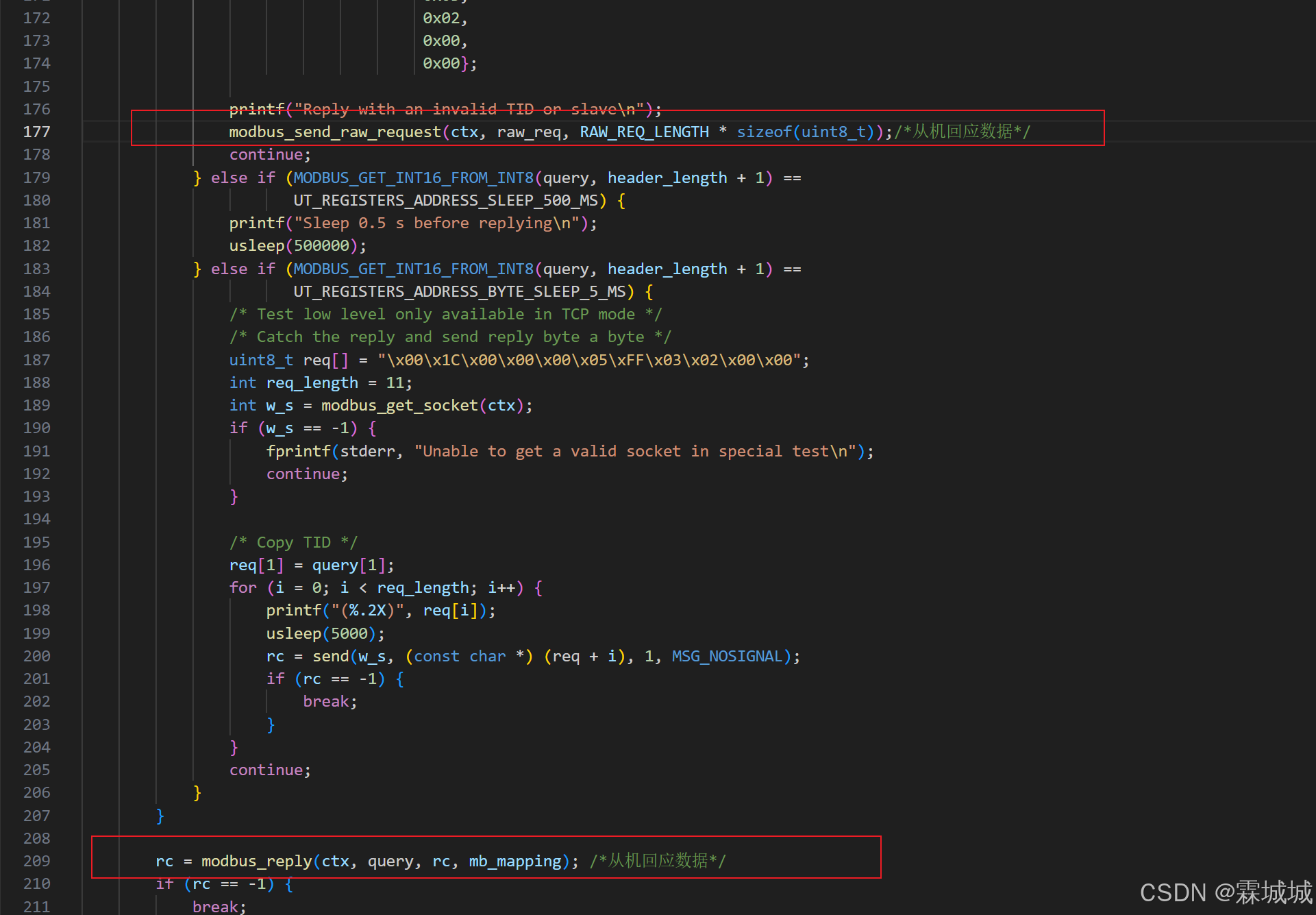
libmodbus 源码学习笔记
1.核心函数_框架_数据结构 整个通信的过程 就是上面这个框架 下面就是具体过程 <1> 主设备 我们首先要初始化 我们要使用的串口 然后 设置我们要访问的哪一个设备 最后打开串口 <2>从机设备 也是我们要初始化我们的串口 然后随后立即设置我们的串口设备地址 最后…...
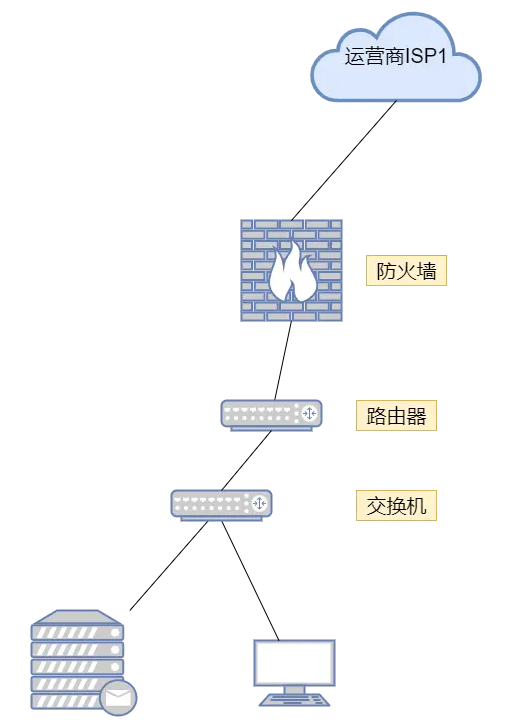
通用网络安全设备之【防火墙】
概念: 防火墙(Firewall),也称防护墙,它是一种位于内部网络与外部网络之间的网络安全防护系统,是一种隔离技术,允许或是限制传输的数据通过。 基于 TCP/IP 协议,主要分为主机型防火…...

Vue.js基础——贼简单易懂!!(响应式 ref 和 reactive、v-on、v-show 和 v-if、v-for、v-bind)
Vue.js是一个渐进式JavaScript框架,用于构建用户界面。它专门设计用于Web应用程序,并专注于视图层。Vue允许开发人员创建可重用的组件,并轻松管理状态和数据绑定。它还提供了一个虚拟DOM系统,用于高效地渲染和重新渲染组件。Vue以…...
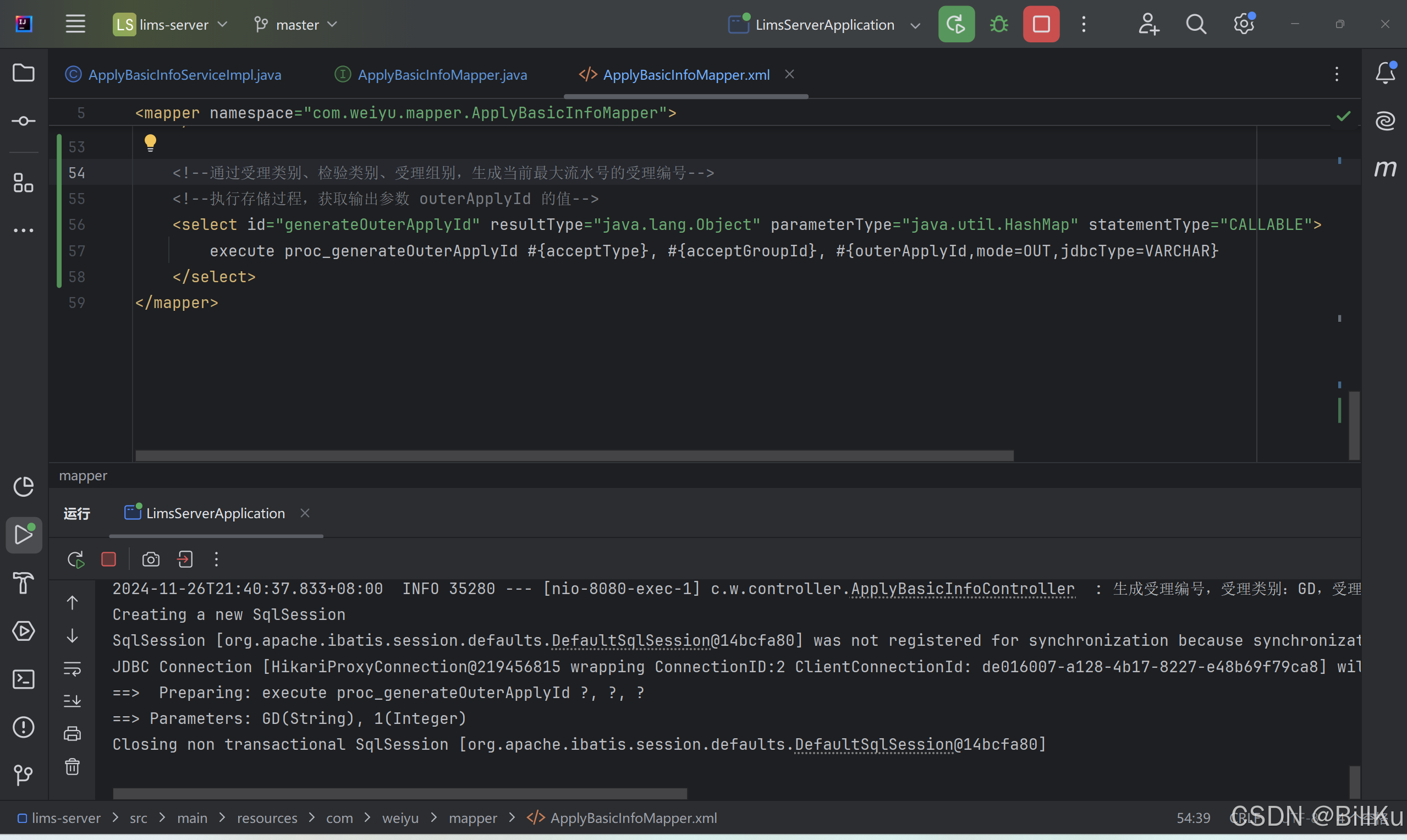
Mybatis 执行存储过程,获取输出参数的值
数据库环境:SQL Server 2008 R2 存储过程 alter procedure proc_generateOuterApplyId acceptType varchar(4),acceptGroupId int,outerApplyId varchar(20) output as begin set nocount onset outerApplyId 24GD6688--select outerApplyId as …...
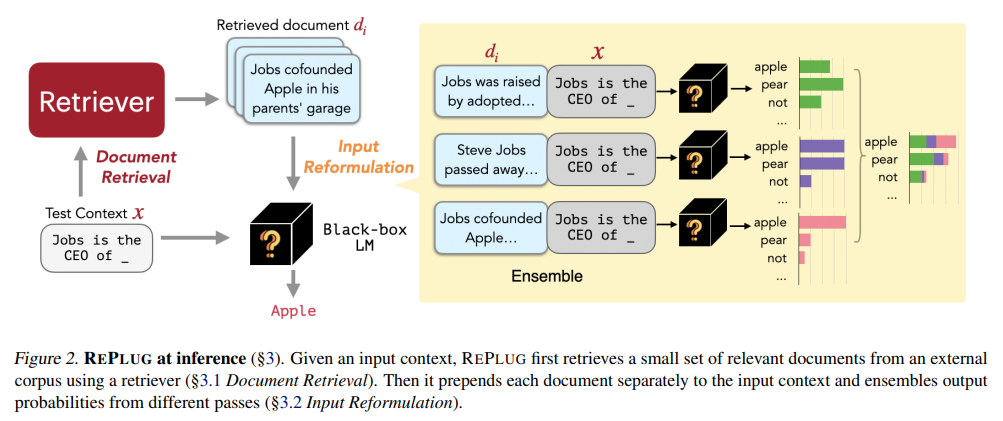
RAG架构类型
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
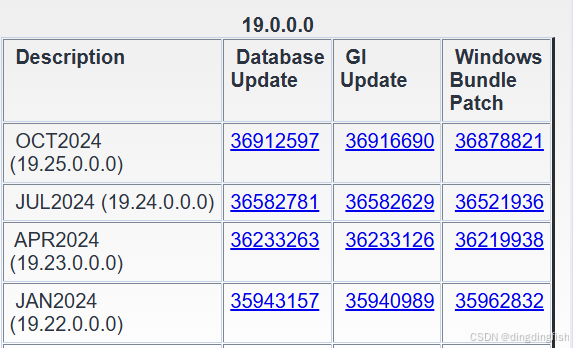
Oracle 数据库 IDENTITY 列的性能选项
在上一篇文章Oracle 数据库 IDENTITY 列中,我们介绍了Oracle IDENTITY列的基础知识。本文将介绍IDENTITY列的几个性能选项。由于IDENTITY列内部使用sequence机制,因此也等同于是sequence的性能选项。 由于sequence是递增的,在高并发时&#…...

计算(a+b)/c的值
计算(ab)/c的值 C语言代码C语言代码Java语言代码Python语言代码 💐The Begin💐点点关注,收藏不迷路💐 给定3个整数a、b、c,计算表达式(ab)/c的值,/是整除运算。 输入 输入仅一行&…...

OpenCV从入门到精通实战(八)——基于dlib的人脸关键点定位
本文使用Python库dlib和OpenCV来实现面部特征点的检测和标注。 下面是代码的主要步骤和相关的代码片段: 步骤一:导入必要的库和设置参数 首先,代码导入了必要的Python库,并通过argparse设置了输入图像和面部标记预测器的参数。…...

unity | 动画模块之卡片堆叠切换
一、预览动画 可以放很多图,可以自己往后加,可以调图片x轴和y轴间距,可以调图片飞出方向,可以调堆叠方向。 图1 图片堆叠动画预览 二、纯净代码 有粉丝问我这个效果,最近很忙,没有时间细写,先…...

前端开发工程师需要学什么?
前端开发工程师需要学习的主要内容包括HTML、CSS、JavaScript、前端框架、响应式设计、性能优化、版本控制等。 HTML/CSS/JavaScript HTML:是网页的骨架,负责网页的结构和内容。CSS:用于美化网页,设计样式和布局。…...

网络常见命令
一.添加ip地址 (1)先进入端口号 interface 端口号 (2)添加ip地址 IP address xxx.xxx.x.x 主机位 二、查看路由表(查看192.168.3.1) display ip routing-table 192.168.3.1 三、宣告(宣告完后…...

logminer挖掘日志归档查找问题
--根据发生问题时间点查找归档文件 select first_time,NAME from gv$archived_log where first_time>2016-03-15 17:00:00 and first_time<2016-03-15 21:00:00; 2016-03-15 17:23:55 ARCH/jxdb/archivelog/2016_03_15/thread_1_seq_41588.4060.906577337 2016-03-15 17:…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...