群论入门笔记
群的基本定义
群由一组元素 G 和一个运算(常用符号包括 +,x , 或 ∗)组成。
封闭性
对于任意两个元素 x,y∈G,运算 x * y 的结果仍然属于集合 G,即:
∀x,y∈G,x∗y∈G.
结合律
对于任意 a,b,c∈G,群的运算满足结合律:
(a * b) * c = a * (b * c).
单位元
群中存在一个单位元 e∈G,使得对于任意 y∈G:
y * e = e * y = y.
逆元
对于每个 x∈G,存在逆元 x−1∈G,使得:
x∗x−1=e.
群的注意事项
非交换性
一个群 G 不一定是交换的,即运算可能不满足:
x * y = y * x.
例如,在三角形的变换中,旋转 rr 和翻转 ff 的次序可能影响结果:
特殊情况
- 如果 G 是交换的(即运算满足交换律),称为交换群或阿贝尔群。
- 如果 G 不满足交换律,则称为非交换群或非阿贝尔群。
什么是子群?
子群是由一个群的子集构成的更小的群。子群本身需要满足群的定义。如果 H 是 G 的子群,我们记作 H≤G。
子群的判定条件
要判断一个集合 H 是否是 G 的子群,需要满足以下条件:
- 非空子集:H≠∅,子群中至少要包含一个 G 的元素,通常包括单位元 e。
- 闭合性:如果 a,b∈H,则 a∗b∈H。
- 逆元存在性:对于 H 中的每个元素 a,其逆元 a−1 也必须属于 H。
子群测试法
一个简便的判定方法是验证:
- H≠∅,且
- 对于所有 a,b∈H,都有 a∗b−1∈H。
子群的例子
平凡子群
每个群 G 至少有两个子群:
{e},G.
真子群
如果 H≠G 且 H≠{e},则称 H 为真子群。
整数加法群的子群
在整数群 G=(Z,+)中,子群
Hn={nk:k∈Z},
其中 n 是任意正整数。例如:
H2={0,±2,±4,… }.
陪集与子群的指数
如果 H≤G,那么 H 在 G 中的陪集定义为:
gH={g∗h:h∈H}
其中 g∈G。
H 的指数(记作 ∣G:H∣)是 H 在 G 中不同陪集的数量。
什么是Cayley表?
Cayley表(或称群表)是群论中的一个基本工具,用于表示有限群的结构。它是一个方形矩阵,用来直观地展示群的运算。在Cayley表中,群的每个元素在行和列中都有表示,表中第 ii 行和第 jj 列的交点显示了元素 gi 和 gj 经群运算后的结果。
如何构建Cayley表
考虑一个有限群 G,它的元素为 {g1,g2,…,gn},群的二元运算为 * 。构建该群的Cayley表的步骤如下:
-
标记行和列
用群的元素 g1,g2,…,gn 标记行和列。 -
填充表格
对于每一对元素 gi 和 gj,计算它们的积 gi ∗ gj(根据群的运算规则),并将结果填入表格中对应的位置。 -
对称性
如果群是交换群(即运算是交换的),则Cayley表相对于对角线是对称的。换句话说,对于任意的 gi,gj ∈G,都有:因此表中位置 (i, j) 和 (j, i) 的值相同。
Cayley表的例子
考虑群 Z3={0,1,2},其运算为模3加法(运算到十进制的“3”回到0,也就是求对3求余数)。这个群的Cayley表如下:
行和列标记为 0,1,2。 运算为模3加法,意味着加法结果取模3。
表格中第1行第2列的值是 1 + 2 = 0(模3),因此该项为0。类似地,第2行第3列的值是 2 + 2 = 1(模3)。
Cayley表的性质
单位元
群的单位元 e 会出现在Cayley表的对角线上。这是因为对于任意的 gi,都有:
逆元
每个群元素都有逆元,Cayley表可以用来找到这些逆元。对于元素 gi ,存在元素 gj ,使得:
gi∗gj = e.
交换群
对于交换群(阿贝尔群),Cayley表是对称的。这种对称性反映了对于任意的两个元素 gi 和 gj,都有:
非交换群
对于非交换群(非阿贝尔群),Cayley表通常不是对称的。表中 和
的值会不同。
Cayley表的应用
-
可视化群的结构
Cayley表是一种直观的方式来展示群的结构,尤其是在处理小型有限群时非常有用。它提供了一种快速检查群的封闭性、单位元和逆元的方法。 -
确定群的性质
通过检查Cayley表,可以快速判断群是否是交换的,找出元素的阶,以及识别子群。 -
群的分类
Cayley表还可以帮助分类有限群。例如,通过比较不同群的表,可以判断两个群是否同构(即结构上相同)。
总结
群论是数学中一门研究群及其性质的学科,广泛应用于代数、几何、物理学等多个领域。群的基本定义包括封闭性、结合律、单位元和逆元,构成了群的核心特性。群论的研究不仅限于群本身,还包括群的结构、子群、陪集以及群的表示等内容。
通过对群的不同特性的分析,我们可以将群分为交换群和非交换群。交换群满足运算的交换律,而非交换群则不满足交换律。子群是群的一个重要概念,具有独立的群结构,并且可以通过特定的条件来判断一个集合是否为某个群的子群。子群的分析有助于深入理解群的结构和性质。
Cayley表作为群的一个重要工具,能够直观地展示群的运算规则,尤其适用于有限群。通过Cayley表,我们可以清晰地看到群的元素之间的相互关系,以及群是否具有交换性。此外,Cayley表还帮助我们找到单位元和逆元,为群的性质分析提供了便利。
群论不仅在纯数学中占据重要地位,而且在物理学、化学、密码学等领域有着广泛的应用。在物理学中,群论帮助我们理解对称性和守恒定律;在化学中,群论用于研究分子的对称性;在密码学中,群论是加密算法的基础。
总之,群论为我们提供了分析和理解数学结构的强大工具。通过群的理论,我们能够系统地探索代数结构的内在规律,从而为进一步的数学研究和实际应用提供了理论支持。
相关文章:
群论入门笔记
群的基本定义 群由一组元素 G 和一个运算(常用符号包括 ,x , 或 ∗)组成。 封闭性 对于任意两个元素 x,y∈G,运算 x * y 的结果仍然属于集合 G,即: ∀x,y∈G,x∗y∈G. 结合律 对于任意 a,b,c∈G&…...

2024最新python使用yt-dlp
2024最新python使用yt-dlp下载YT视频 1.获取yt的cookie1)google浏览器下载Get cookies.txt LOCALLY插件2)导出cookie 2.yt-dlp下载[yt-dlp的GitHub地址](https://github.com/yt-dlp/yt-dlp?tabreadme-ov-file)1)使用Pycharm(2024.3)进行代码…...

Python + 深度学习从 0 到 1(00 / 99)
希望对你有帮助呀!!💜💜 如有更好理解的思路,欢迎大家留言补充 ~ 一起加油叭 💦 欢迎关注、订阅专栏 【深度学习从 0 到 1】谢谢你的支持! ⭐ 什么是深度学习? 人工智能、机器学习与…...

单点登录深入详解之设计方案总结
基于cookie的单点登录解决方案 概述 用户登录之后 , 将认证信息存储至 Cookie ,当再次访问本服务或者访问其他应用服务时,直接从 Cookie 中传递认证信息,进行鉴权处理。 问题 1. 如何保障Cookie内用户认证信息的安全性? 第一, Cookie…...

Loadsh源码分析-forEach,eachRight,map,flatMap,flatMapDeep,flatMapDepth
处理数组array的函数已经学习完,接下来是collection相关的函数, collection指的是一组用于处理集合(如数组或对象)的工具函数。 lodash源码研读之forEach,forEachRight,map,flatMap,flatMapDeep,flatMapDepth 一、源码地址 GitH…...

检测到“runtimelibrary”的不匹配项: 值“mtd_staticdebug”不匹配值“mdd_dynamic”
1. 解释“runtimelibrary”不匹配错误的含义 在Visual Studio中,LNK2038错误表示链接器检测到项目与其依赖的库之间存在“Runtime Library”(运行时库)的不匹配。具体来说,这意味着编译项目时使用的运行时库类型与编译依赖库时使…...

go clean -modcache命令清理缓存
go clean -modcache命令用于清理Go模块的本地缓存。Go模块缓存位于$GOPATH/pkg/mod/cache目录下,存储了所有下载和使用的模块版本。当执行go clean -modcache时,这个命令会删除该目录下的所有内容,迫使Go在下次构建时重新下载所有依赖的模块。…...

C#结构体排序(数组)
结构体排序(数组) 1 示例1.1 以PointF为例展示效果1.2 运行结果展示 2实际运用2.1 创建结构体2.2 调用示例2.3 运行结果展示 1 示例 1.1 以PointF为例展示效果 private void button1_Click(object sender, EventArgs e) {Random random new Random();…...

基于边缘智能网关的机房安全监测应用
随着我国工业互联网的扎实推进,越来越多地区积极建设信息基础设施,以充沛算力支撑产业物联网的可持续发展,数据机房就是其中的典型代表。而且随着机房规模的扩大,对于机房的安全管理难题挑战也日益增加。 面向数据机房安全监测与管…...

【Jenkins】自动化部署 maven 项目笔记
文章目录 前言1. Jenkins 新增 Maven 项目2. Jenkins 配置 Github 信息3. Jenkins 清理 Workspace4. Jenkins 配置 后置Shell脚本后记 前言 目标:自动化部署自己的github项目 过程:jenkins 配置、 shell 脚本积累 相关连接 Jenkins 官方 docker 指导d…...

LeetCode 3243. Shortest Distance After Road Addition Queries I
🔗 https://leetcode.com/problems/shortest-distance-after-road-addition-queries-i 题目 有 n 个城市,编号 0 ~ n-1,从城市 i 到 i1 有一条路给若干高速路,表明从城市 u 到 v 有一条新增的路,v - u > 1返回每新…...

ML 系列:第 31 节— 机器学习中的协方差和相关性
文章目录 一、说明二、协方差和相关性2.1 协方差的概念2.1 相关 三、有关关联的高级主题 (有关详细信息)3.1 相关性和独立性3.2 零相关性和依赖性示例 四、相关性和因果关系五、结论 一、说明 协方差量化了两个随机变量协同变化的程度。当一个变量的较高…...

【鸿蒙】鸿蒙开发过程中this指向问题
文章目录 什么是 this?常见 this 指向问题案例分析:HarmonyOS 组件中的 this 指向问题问题描述问题分析原因 解决方案:绑定 this 的正确方法方法一:使用箭头函数方法二:手动绑定 this 完整代码示例使用箭头函数使用 bi…...

d3-contour 生成等高线图
D3.js 是一个强大的 JavaScript 库,用于创建动态、交互式数据可视化。d3-contour 是 D3.js 的一个扩展模块,用于生成等高线图(contour plots)。 属性和方法 属性 x: 一个函数,用于从数据点中提取 x 坐标。y: 一个函…...

Ubuntu20.04离线安装全教程(包括DellR940重置Raid 5、安装Ubuntu、设置root、安装nvidia英伟达显卡驱动及设置防火墙白名单)
本文记录重装Ubuntu20.04的所有记录,从服务器磁盘阵列重新排列、Ubuntu 20.04系统安装、配置root权限、安装Nvidia显卡驱动以及设置防火墙白名单的全部操作。 每一部分参考的博客的出处会放置于段落末尾,表示感谢! 一、重置服务器磁盘阵列&…...
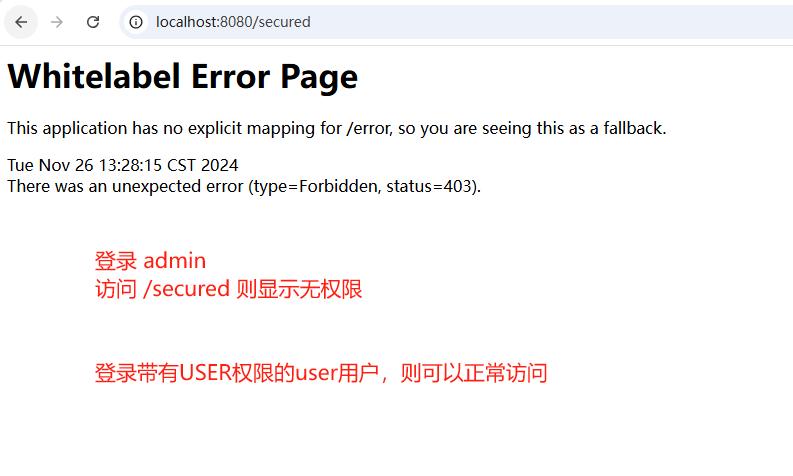
Spring Boot 3 集成 Spring Security(2)授权
文章目录 授权配置 SecurityFilterChain基于注解的授权控制自定义权限决策 在《Spring Boot 3 集成 Spring Security(1)》中,我们简单实现了 Spring Security 的认证功能,通过实现用户身份验证来确保系统的安全性。Spring Securit…...

【开篇】.NET开源 ORM 框架 SqlSugar 系列
01. 前言 ☘️ 1.1 什么是ORM? 对象-关系映射(Object-Relational Mapping,简称ORM),面向对象的开发方法是当今企业级应用开发环境中的主流开发方法,关系数据库是企业级应用环境中永久存放数据的主流数据存储系统。对…...

参加面试被问到的面试题
1.在程序中如何开启事务? 在Java中,使用JDBC(Java Database Connectivity)与数据库交互时,你可以使用Connection对象的setAutoCommit方法来控制事务。默认情况下,autoCommit是开启的,这意味着每…...

第29天:安全开发-JS应用DOM树加密编码库断点调试逆向分析元素属性操作
时间轴: 演示案例: JS 原生开发-DOM 树-用户交互 DOM:文档操作对象 浏览器提供的一套专门用来操作网页代码内容的功能,实现自主或用户交互动作反馈 安全问题:本身的前端代码通过 DOM 技术实现代码的更新修改ÿ…...

react 的路由功能
1. 安装依赖 pnpm add react-router-dom 2. 基本的路由设置(BrowserRouter) 在 main.tsx 入口文件中使用BrowserRouter组件来包裹整个应用。它会监听浏览器的 URL 变化。 import { StrictMode } from "react";import { createRoot } from …...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
