利用编程思维做题之最小堆选出最大的前10个整数
1. 理解问题
我们需要设计一个程序,读取 80,000 个无序的整数,并将它们存储在顺序表(数组)中。然后从这些整数中选出最大的前 10 个整数,并打印它们。要求我们使用时间复杂度最低的算法。
由于数据量很大,直接排序的时间复杂度较高,因此我们需要一个更高效的算法。最小堆 是一种合适的选择,因为它能够在 O(n log k) 的时间复杂度内完成最大 10 个整数的选取。
2. 输入输出
- 输入:通过键盘输入 80,000 个整数。
- 输出:打印出最大的 10 个整数。
3. 数据结构
我们使用一个最小堆来存储当前最大 10 个数。堆的根节点是堆中最小的元素,插入新元素时,如果新元素大于堆的根节点,则替换根节点并调整堆结构。这样,在遍历完所有 80,000 个数之后,堆中的 10 个元素就是最大的 10 个整数。
最小堆的数据结构如下:
struct MinHeap {
int* arr; // 存储堆的数组
int size; // 当前堆的大小
int capacity; // 堆的最大容量
};
4. 制定策略
- 建堆:我们通过一个大小为 10 的最小堆来存储当前最大的 10 个数。
- 遍历输入:每读取一个数,检查该数是否大于堆顶元素,如果大于,则替换堆顶并调整堆。
- 输出结果:遍历完所有数后,堆中将包含最大的 10 个数。
- 时间复杂度:由于堆的操作是 O(log k),每次插入操作的时间复杂度为 O(log 10),因此整个过程的时间复杂度是 O(n log 10) ≈ O(n)。
5. 实现代码
5.1 完整代码
#include <stdio.h>
#include <stdlib.h>
// 最小堆的结构体定义
struct MinHeap {
int* arr; // 存储堆的数组
int size; // 当前堆的大小,即有数值的个数
int capacity; // 堆的最大容量
};
// 创建最小堆
struct MinHeap* createMinHeap(int capacity) {
// 定义一个MinHeap结构体大小的指针,指向一个堆
struct MinHeap* heap = (struct MinHeap*)malloc(sizeof(struct MinHeap));
heap->arr = (int*)malloc(sizeof(int) * capacity);
heap->size = 0;
heap->capacity = capacity;
return heap;
}
// 交换两个元素
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 维护堆的性质(向下调整)
void heapify(struct MinHeap* heap, int index) {
int left = 2 * index + 1;
int right = 2 * index + 2;
int smallest = index;
// 找出最小的元素
if (left < heap->size && heap->arr[left] < heap->arr[smallest]) {
smallest = left;
}
if (right < heap->size && heap->arr[right] < heap->arr[smallest]) {
smallest = right;
}
// 如果最小元素不是当前元素,交换并继续调整
if (smallest != index) {
swap(&heap->arr[index], &heap->arr[smallest]);
heapify(heap, smallest);
}
}
// 维护堆的性质(向上调整)
void upheapify(struct MinHeap* heap, int index) {
while (index > 0 && heap->arr[index] < heap->arr[(index - 1) / 2]) {
swap(&heap->arr[index], &heap->arr[(index - 1) / 2]);
index = (index - 1) / 2;
}
}
// 插入元素到堆中
void insert(struct MinHeap* heap, int value) {
if (heap->size < heap->capacity) {
// 如果堆未满,直接插入
heap->arr[heap->size] = value;
upheapify(heap, heap->size); // 插入后需要向上调整
heap->size++;
} else if (value > heap->arr[0]) {
// 如果堆已满且当前值大于堆顶元素,则替换堆顶
heap->arr[0] = value;
heapify(heap, 0); // 替换堆顶后需要进行堆化
}
}
// 打印堆中的前 10 个最大值
void printTop10(struct MinHeap* heap) {
// 最小堆中的前 10 个最大值已经存储在堆中,直接打印
for (int i = 0; i < heap->size; i++) {
printf("%d ", heap->arr[i]);
}
printf("\n");
}
// 主程序
int main() {
struct MinHeap* heap = createMinHeap(10); // 创建一个容量为 10 的最小堆
int value;
printf("请输入 80000 个整数(每输入一个整数后按 Enter,输入 80000 个数):\n");
// 读取 80,000 个整数
for (int i = 0; i < 80000; i++) {
scanf("%d", &value);
insert(heap, value); // 将输入的值插入堆中
}
// 打印堆中的前 10 个最大值
printf("最大的 10 个整数是:\n");
printTop10(heap);
// 释放堆内存
free(heap->arr);
free(heap);
return 0;
}
6. 代码说明
- 结构体定义:我们定义了一个
MinHeap结构体来表示最小堆,包含一个数组arr存储堆的元素,size表示当前堆的大小,capacity是堆的最大容量(即 10)。 - 堆的操作:
createMinHeap:创建一个新的最小堆。swap:交换堆中的两个元素。heapify:维护堆的性质,确保堆仍然是最小堆。insert:将新元素插入堆。如果堆未满,直接插入。如果堆已满并且新元素大于堆顶元素,则替换堆顶并重新调整堆。printTop10:打印堆中的前 10 个最大值(即堆中的元素)。
- 主程序:
- 通过
scanf读取 80,000 个整数,并将它们插入最小堆。 - 插入操作将保证堆中始终保存着最大的 10 个元素。
- 最后输出堆中的元素,即为最大的 10 个整数。
- 通过
7. 模拟过程
假设输入为:
2 5 8 12 20 10 1 35 27 50 41 39 70 80 90 23 17 16 13 11 ...
程序将使用最小堆的结构,维护堆中最大 10 个数。每读取一个新数,程序将插入最小堆,并保证堆的大小不超过 10。当所有 80,000 个数输入完成后,堆中将包含最大的 10 个数。
8. 运行结果
假设输入的数据中最大的 10 个数为:90, 80, 70, 50, 41, 39, 35, 27, 23, 20,程序输出:
最大的 10 个整数是:90 80 70 50 41 39 35 27 23 20
注意,此代码只会获取最大的10个数,但不会排序这10个数。
9. 时间和空间复杂度分析
- 时间复杂度:
- 建堆的时间复杂度:每次插入一个元素时,最小堆的插入操作为 O(log 10) = O(1),因此整个过程的时间复杂度是 O(n),其中
n为 80,000。
- 建堆的时间复杂度:每次插入一个元素时,最小堆的插入操作为 O(log 10) = O(1),因此整个过程的时间复杂度是 O(n),其中
- 空间复杂度:最小堆需要 O(10) 的空间来存储最大 10 个数,因此空间复杂度为 O(1),即常数空间。
10. 总结
通过使用最小堆,我们能够以 O(n) 的时间复杂度找到并输出最大的 10 个数。这种方法比直接排序更高效,尤其是当数据量很大时。
相关文章:

利用编程思维做题之最小堆选出最大的前10个整数
1. 理解问题 我们需要设计一个程序,读取 80,000 个无序的整数,并将它们存储在顺序表(数组)中。然后从这些整数中选出最大的前 10 个整数,并打印它们。要求我们使用时间复杂度最低的算法。 由于数据量很大,直…...

详解MVC架构与三层架构以及DO、VO、DTO、BO、PO | SpringBoot基础概念
🙋大家好!我是毛毛张! 🌈个人首页: 神马都会亿点点的毛毛张 今天毛毛张分享的是SpeingBoot框架学习中的一些基础概念性的东西:MVC结构、三层架构、POJO、Entity、PO、VO、DO、BO、DTO、DAO 文章目录 1.架构1.1 基本…...

Unity C# 影响性能的坑点
c用的时间长了怕unity的坑忘了,记录一下。 GetComponent最好使用GetComponent<T>()的形式, 继承自Monobehaviour的函数要避免空的Awake()、Start()、Update()、FixedUpdate().这些空回调会造成性能浪费 GetComponent方法最好避免在Update当中使用…...

工作学习:切换git账号
概括 最近工作用的git账号下发下来了,需要切换一下使用的账号。因为是第一次弄,不熟悉,现在记录一下。 打开设置 路径–git—git remotes,我这里选择项是Manage Remotes,点进去就可以了。 之后会出现一个输入框&am…...
)
量化交易系统开发-实时行情自动化交易-8.量化交易服务平台(一)
19年创业做过一年的量化交易但没有成功,作为交易系统的开发人员积累了一些经验,最近想重新研究交易系统,一边整理一边写出来一些思考供大家参考,也希望跟做量化的朋友有更多的交流和合作。 接下来会对于收集整理的33个量化交易服…...

Scala习题
姓名,语文,数学,英语 张伟,87,92,88 李娜,90,85,95 王强,78,90,82 赵敏,92,88,91 孙涛,…...

结构方程模型(SEM)入门到精通:lavaan VS piecewiseSEM、全局估计/局域估计;潜变量分析、复合变量分析、贝叶斯SEM在生态学领域应用
目录 第一章 夯实基础 R/Rstudio简介及入门 第二章 结构方程模型(SEM)介绍 第三章 R语言SEM分析入门:lavaan VS piecewiseSEM 第四章 SEM全局估计(lavaan)在生态学领域高阶应用 第五章 SEM潜变量分析在生态学领域…...

OpenCV图像基础处理:通道分离与灰度转换
在计算机视觉处理中,理解图像的颜色通道和灰度表示是非常重要的基础知识。今天我们通过Python和OpenCV来探索图像的基本组成。 ## 1. 图像的基本组成 在数字图像处理中,彩色图像通常由三个基本颜色通道组成: - 蓝色(Blue&#x…...

C++ 类和对象(类型转换、static成员)
目录 一、前言 二、正文 1.隐式类型转换 1.1隐式类型转换的使用 2.static成员 2.1 static 成员的使用 2.1.1static修辞成员变量 2.1.2 static修辞成员函数 三、结语 一、前言 大家好,我们又见面了。昨天我们已经分享了初始化列表:https://blog.c…...
【网络安全设备系列】12、态势感知
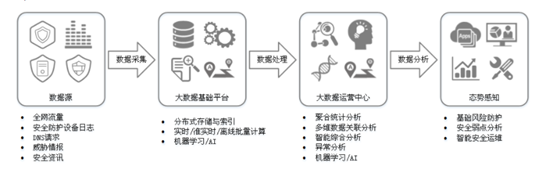
0x00 定义: 态势感知(Situation Awareness,SA)能够检测出超过20大类的云上安全风险,包括DDoS攻击、暴力破解、Web攻击、后门木马、僵尸主机、异常行为、漏洞攻击、命令与控制等。利用大数据分析技术,态势感…...

Linux介绍与安装指南:从入门到精通
1. Linux简介 1.1 什么是Linux? Linux是一种基于Unix的操作系统,由Linus Torvalds于1991年首次发布。Linux的核心(Kernel)是开源的,允许任何人自由使用、修改和分发。Linux操作系统通常包括Linux内核、GNU工具集、图…...

BGE-M3模型结合Milvus向量数据库强强联合实现混合检索
在基于生成式人工智能的应用开发中,通过关键词或语义匹配的方式对用户提问意图进行识别是一个很重要的步骤,因为识别的精准与否会影响后续大语言模型能否检索出合适的内容作为推理的上下文信息(或选择合适的工具)以给出用户最符合…...
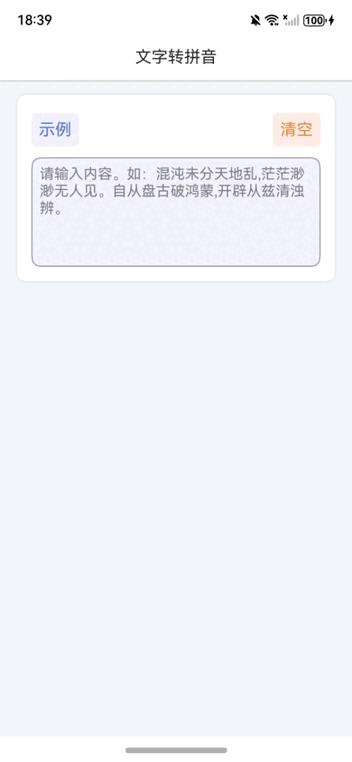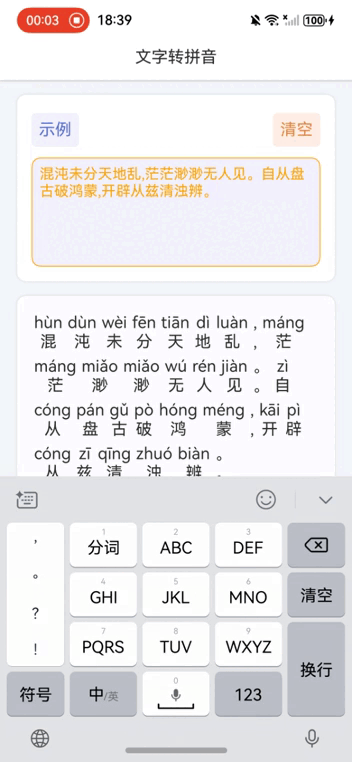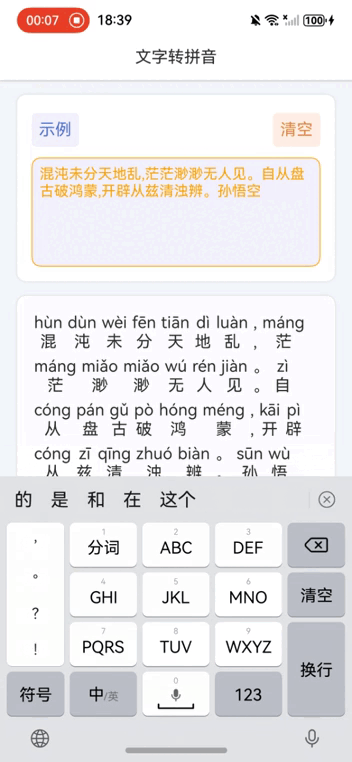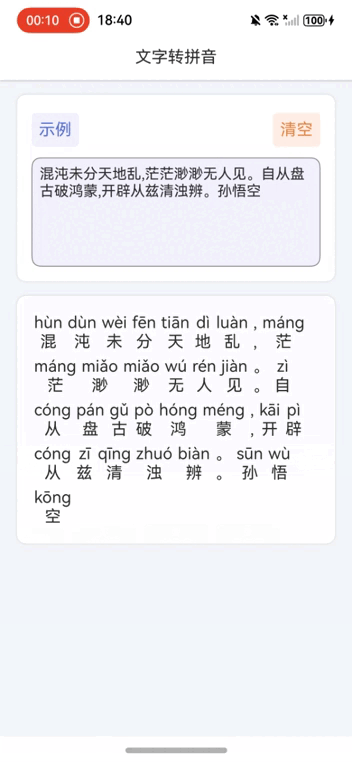
鸿蒙NEXT开发案例:文字转拼音
【引言】 在鸿蒙NEXT开发中,文字转拼音是一个常见的需求,本文将介绍如何利用鸿蒙系统和pinyin-pro库实现文字转拼音的功能。 【环境准备】 • 操作系统:Windows 10 • 开发工具:DevEco Studio NEXT Beta1 Build Version: 5.0.…...
)
CTF之密码学(栅栏加密)
栅栏密码是古典密码的一种,其原理是将一组要加密的明文划分为n个一组(n通常根据加密需求确定,且一般不会太大,以保证密码的复杂性和安全性),然后取每个组的第一个字符(有时也涉及取其他位置的字…...

修改插槽样式,el-input 插槽 append 的样式
需缩少插槽 append 的 宽度 方法1、使用内联样式直接修改,指定 width 为 30px <el-input v-model"props.applyBasicInfo.outerApplyId" :disabled"props.operateCommandType input-modify"><template #append><el-button click…...

UPLOAD LABS | PASS 01 - 绕过前端 JS 限制
关注这个靶场的其它相关笔记:UPLOAD LABS —— 靶场笔记合集-CSDN博客 0x01:过关流程 本关的目标是上传一个 WebShell 到目标服务器上,并成功访问: 我们直接尝试上传后缀为 .php 的一句话木马: 如上,靶场弹…...

【css实现收货地址下边的平行四边形彩色线条】
废话不多说,直接上代码: <div class"address-block" ><!-- 其他内容... --><div class"checked-ar"></div> </div> .address-block{height:120px;position: relative;overflow: hidden;width: 500p…...

缓存方案分享
不知道大家平常更新缓存是怎么做的,但是大部分时候都是更新数据的同时更新缓存,今天和同事一起聊到一个缓存方案的问题,感觉很有趣、非常精妙,记录一下。 基于此本文将介绍几种常见的缓存更新策略,包括简单的缓存覆盖…...

第四十篇 DDP模型并行
摘要 分布式数据并行(DDP)技术是深度学习领域中的一项重要技术,它通过将数据和计算任务分布在多个计算节点上,实现了大规模模型的并行训练。 DDP技术的基本原理是将数据和模型参数分割成多个部分,每个部分由一个计算节点负责处理。在训练过程中,每个节点独立计算梯度,…...

软件测试面试之常规问题
1.描述一下测试过程 类似题目:测试的生命周期 思路:这是一个“范围”很大的题目,而且回答时间一般在3分钟之内,不可能非常详细的描述整个过程,因此答题的思路要从整体结构入手,不要过细。为了保证答案的准确性,可以引…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
