STL算法之set相关算法
STL一共提供了四种与set(集合)相关的算法,分别是并集(union)、交集(intersection)、差集(difference)、对称差集(symmetric difference)。
目录
set_union
set_itersection
set_difference
set_symmetric_difference
所谓set,可细分为数学上定义的和STL的定义两种,数学上的set允许元素重复而未经排序,例如{1,1,4,6,3},STL的定义(也就是set容器)则要求元素不得重复,并且经过排序,例如{1,3,4,6}。本节的四个算法所接受的set,必须是有序区间(sorted range),元素值可重复出现。换句话说,它们可接受STL的set/multiset容器作为输入区间。
SGI另外提供了hash_set/hash_multiset两种容器,以hashtable为底层机制。其内的元素并未呈现排序状态,所以虽然名称也是set字样,缺不可以应用于本节的四个算法。
本节四个算法都至少有四个参数,分别表现两个set区间,以下所有说明都以S1代表第一区间[first1, last1),以S2代表第二区间[first2, last2).每一个set算法都提供两个版本,第二个版本允许用户指定"a<b"的意义,因为这些算法判断两个元素是否相等的依据,完全靠“小于”运算。
a <b && b< a 推导出 a==b
以下程序测试四个set相关算法。欲使用它们,必须包含<algorithm>
#include <set>
#include <iostream>
#include <algorithm>
#include <iterator>
using namespace std;template <class T>
struct display {void operator() (const T& x) {cout << x << " ";}
};int main() {int ia1[6] = {1, 3, 5, 7, 9, 11};int ia2[7] = {1, 1, 2, 3, 5, 8, 13};multiset<int> S1(ia1, ia1+6);multiset<int> S2(ia2, ia2+7);for_each(S1.begin(), S1.end(), display<int>());// 1 3 5 7 9 11cout << endl;for_each(S2.begin(), S2.end(), display<int>());// 1 1 2 3 5 8 13cout << endl;auto first1 = S1.begin();auto last1 = S1.end();auto first2 = S2.begin();auto last2 = S2.end();cout << "Union of S1 and S2:";set_union(first1, last1, first2, last2, ostream_iterator<int>(cout, " ")); // 1 1 2 3 5 7 9 11 13cout << endl;first1 = S1.begin();first2 = S2.begin();cout << "intersection of S1 and S2:";set_intersection(first1, last1, first2, last2, ostream_iterator<int>(cout, " "));// 1 3 5cout << endl;first1 = S1.begin();first2 = S2.begin();cout << "difference of S1 and S2 (S1-S2): " ;set_difference(first1, last1, first2, last2, ostream_iterator<int>(cout, " ")); // 7 9 11cout << endl;first1 = S1.begin();first2 = S2.begin();cout << "Symmetric difference of S1 and S2: " ;set_symmetric_difference(first1, last1, first2, last2, ostream_iterator<int>(cout, " ")); // 1 2 7 8 9 11 13cout << endl;first1 = S1.begin();first2 = S2.begin();cout << "difference of S2 and S1 (S2-S1): ";set_difference(first2, last2, first1, last1, ostream_iterator<int>(cout, " ")); // 1 2 8 13cout << endl;return 0;
}
执行结果如下:
1 3 5 7 9 11
1 1 2 3 5 8 13
Union of S1 and S2:1 1 2 3 5 7 8 9 11 13
intersection of S1 and S2:1 3 5
difference of S1 and S2 (S1-S2): 7 9 11
Symmetric difference of S1 and S2: 1 2 7 8 9 11 13
difference of S2 and S1 (S2-S1): 1 2 8 13 请注意,当集合(set)允许重复元素的存在时,并集、交集、差集、对称差集的定义,都与直观定义有些微的不同。例如上述的并集结果,我们会直观以为是{1,2,3,5,7,8,9,11,13},而上述的对称差结果,我们会直观以为是{2,7,8,9,11,13},这都是未考虑重复元素的结果。以下各小节会详细说明。
set_union
算法set_union可构造S1、S2之并集。也就是说,它能构造出集合,此集合内含S1或S2内的每一个元素。S1、S2及其并集都是以排序区间表示。返回值为一个迭代器,指向输出区间的尾端。
由于S1和S2内的每一个元素都不需要唯一,因此,如果某个值在S1出现n次,在S2出现m次,那么该值在输出区间会出现max(n,m)次,其中n个来自S1,其余来自S2,在STL set容器内,且
set_union是一种稳定(stable)操作,意思是输入区间内的每个元素的相对顺序都不会改变。set_union有两个版本,差别在于如何定义某个元素小于另一个元素。第一版本使用operator<进行比较,第二版本采用仿函数comp进行比较。
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_union(InputIterator1 first1, InputIterator1 last1,InputIterator2 first2, InputIterator2 last2,OutputIterator result) {while (first1 != last1 && first2 != last2) {if (*first1 < *first2) {*result = *first1;++first1;} else if (*first2 < *first1) {*result = *first2;++first2;} else {*result = *first1;++first1;++first2;}++result;}// 此时[first1,last1)和[first2,last2)至少有一个空白区间,边界剩下的是都属于union的元素return copy(first2, last2, copy(first1, last1, result));
}从以上合并的过程,可以看出主要是利用了set/multi_set经过排序的特性,而后对并集的特例化处理。和数学定义上的union处理略有差异。
set_itersection
算法set_itersection可构造S1,S2之交集。也就是说,它能构造出集合,此集合内含同时出现在S1和S2的每一个元素。S1、S2及其交集都是以排序区间表示。返回值为一个迭代器,指向输出区间的尾端。
由于S1和S2内的每个元素都不需要唯一,因此,如果某个值在S1出现n次,在S2出现m次,那么该值在输出区间出现min(n,m)次,并且全部来自S1.在STL set内,且
。
set_itersection是一种稳定(stable)的操作,意思是输出区间内的每个元素的相对顺序都和S1内的相对顺序相同。它有两个版本,其差异同set_union.其代码定义如下:
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_itersection(InputIterator1 first1, InputIterator1 last1,InputIterator2 first2, InputIterator2 last2,OutputIterator result) {while (first1 != last1 && first2 != last2) {if (*first1 < *first2) {++first1;} else if (*first2 < *first1) {++first2;} else { // *first1 == *first2*result = *first1;++first1;++first2;}++result;}return result;
}对照set_itersection和set_union的算法实现,可发现内部迭代器的前进逻辑是一致的;只是输出时,只讲*first1==*first2的数据输出到result。对于边界情况,因为其中一组迭代器已经为空,所以也就没有了新的元素加入,直接返回了result;
set_difference
算法set_difference可构造S1、S2只差集。也就是说,它能构造集合S1-S2,此集合内容"出现于S1但不出现于S2"的每一个元素。S1、S2及其交集都是以排序区间表示。返回值为一个迭代器,指向输出区间的尾端。
由于S1和S2内的每个元素都不需要唯一,因此,如果某个值在S1出现n次,在S2出现m次,那么该值在输出区间出现max(n-m,0)次
set_difference是一种稳定操作,输出相对顺序保持S1内的相对顺序。代码如下:
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_difference(InputIterator1 first1, InputIterator1 last1,InputIterator2 first2, InputIterator2 last2,OutputIterator result) {while (first1 != last1 && first2 != last2) {if (*first1 < *first2) {*result = *first1;++first1;++result;} else if (*first2 < *first1) {++first2;} else {++first1;++first2;}}return copy(first1, last1, result);
}有了前面set_union及set_itersecion算法的经验,可看出迭代器的逻辑还是保留的相同的步伐。只是输出给result的值,只保留了*first1 < *first2的部分;正好符合S1-S2的特性。
set_symmetric_difference
算法set_symmetric_difference可构造S1、S2之对称差集。也就是构造出,此集合内含"出现在S1但不出现于S2"以及“出现在S2不出现在S1”的每一个元素。
有了前三个算法的基础,很容易得出set_symmetric_difference的结果包含*first1<*first2,以及*first2-*first1的结果,同时需要将边界情况保留。其代码如下:
template <class InputIterator1, class InputIterator2, class OutputIterator>
OutputIterator set_symmetric_difference(InputIterator1 first1, InputIterator1 last1,InputIterator2 first2, InputIterator2 last2,OutputIterator result) {while (first1 != last1 && first2 != last2) {if (*first1 < *first2) {*result = *first1;++first1;++result;} else if (*first2 < *first1) {*result = *first2++first2;++result;} else {++first1;++first2;}}return copy(first2, last2, copy(first1, last1, result));
}
相关文章:
STL算法之set相关算法
STL一共提供了四种与set(集合)相关的算法,分别是并集(union)、交集(intersection)、差集(difference)、对称差集(symmetric difference)。 目录 set_union set_itersection set_difference set_symmetric_difference 所谓set,可细分为数学上定义的和…...

vscode中json文件的注释飘红
vscode的json文件 添加注释,提示json中不允许有注释,点编辑器最下面的json,如下图 然后选择如上图的json with comments就好了...

【微服务】SpringBoot 整合Redis Stack 构建本地向量数据库相似性查询
目录 一、前言 二、向量数据库介绍 2.1 什么是向量数据库 2.2 向量数据库特点 2.3 向量数据库使用场景 三、常用的向量数据库解决方案 3.1 Milvus 3.1.1 Milvus是什么 3.1.2 Milvus主要特点 3.2 Faiss 3.2.1 Faiss是什么 3.2.2 Faiss主要特点 3.3 Pinecone 3.3.1 …...

三:安装服务-controller node
一:工具、环境准备-controller node 二:OpenStack环境准备-controller node 三:安装服务-controller node 四:工具、环境准备-compute node 五:OpenStack环境准备-compute node 六:安装服务-compute node 七…...
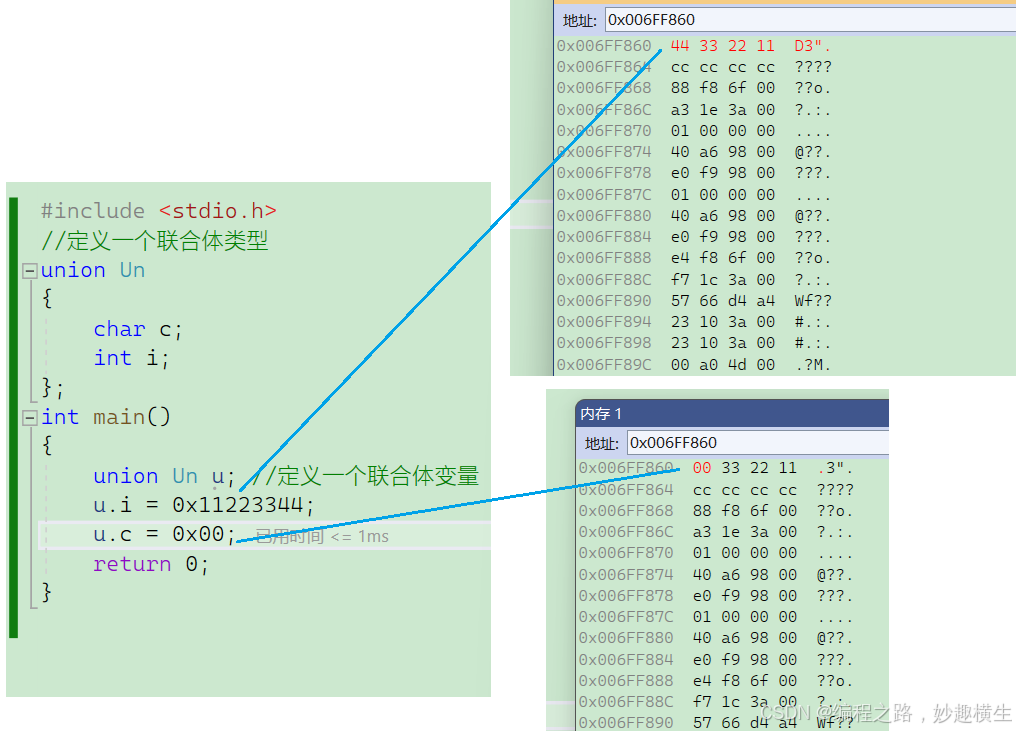
自定义类型: 结构体、枚举 、联合
目录 结构体 结构体类型的声明 匿名结构体 结构的自引用 结构体变量的定义和初始化 结构体成员变量的访问 结构体内存对齐 结构体传参 位段 位段类型的声明 位段的内存分配 位段的跨平台问题 位段的应用 枚举 枚举类型的定义 枚举的优点 联合体(共用体) 联合…...
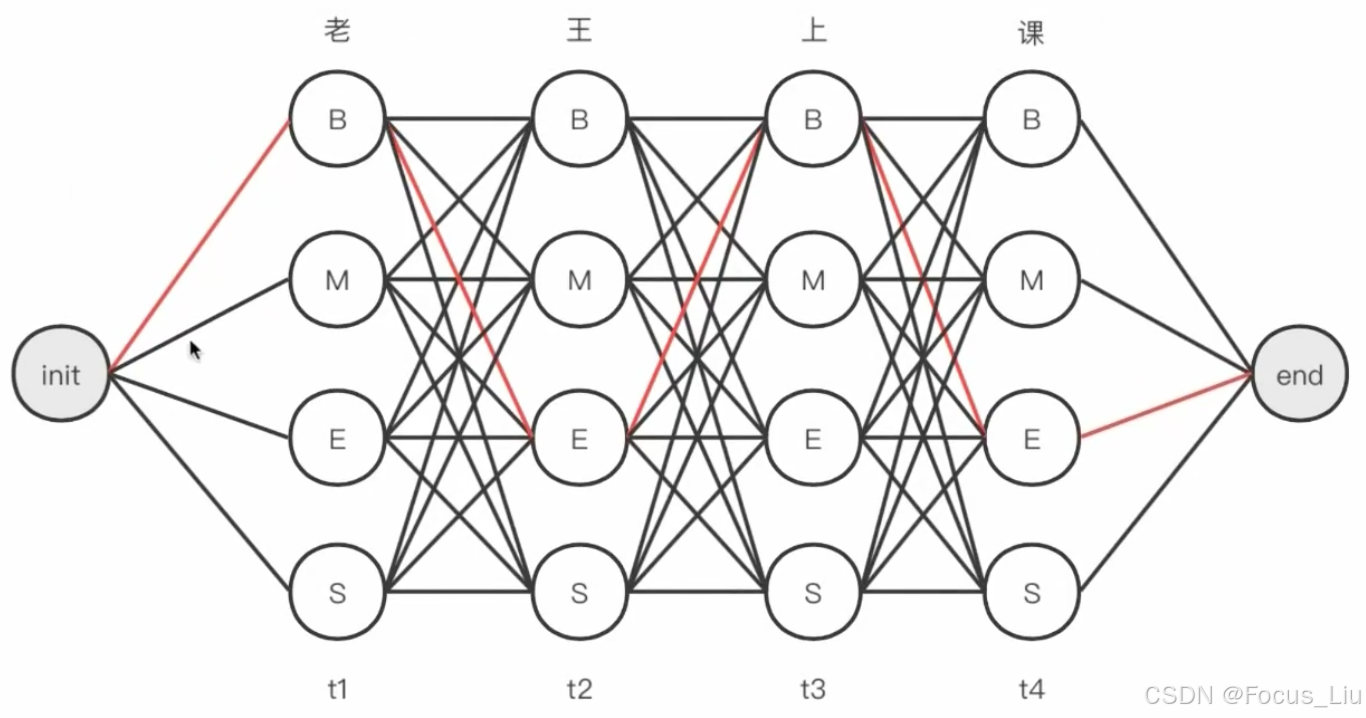
Bert+CRF的NER实战
CRF(条件随机场-Conditional Random Field) 原始本文:我在北京吃炸酱面 标注示例: 我O在O北B-PLA京I-PLA吃O炸B-FOOD酱I-FOOD面I-FOOD CRF: 目的:提出一些不可能出现的预测组合(例如I-PLA不能…...

永久停用PostgreSQL 归档功能
文章目录 引言永久停用归档功能归档的优势归档的劣势开启归档的情况关闭归档的情况see also引言 PostgreSQL 是一个开源的关系型数据库系统,支持数据归档(WAL),可以实现数据备份、恢复和灾难恢复等功能。在使用 PostgreSQL 的过程中,如果 PostgreSQL 数据库开启了归档(a…...
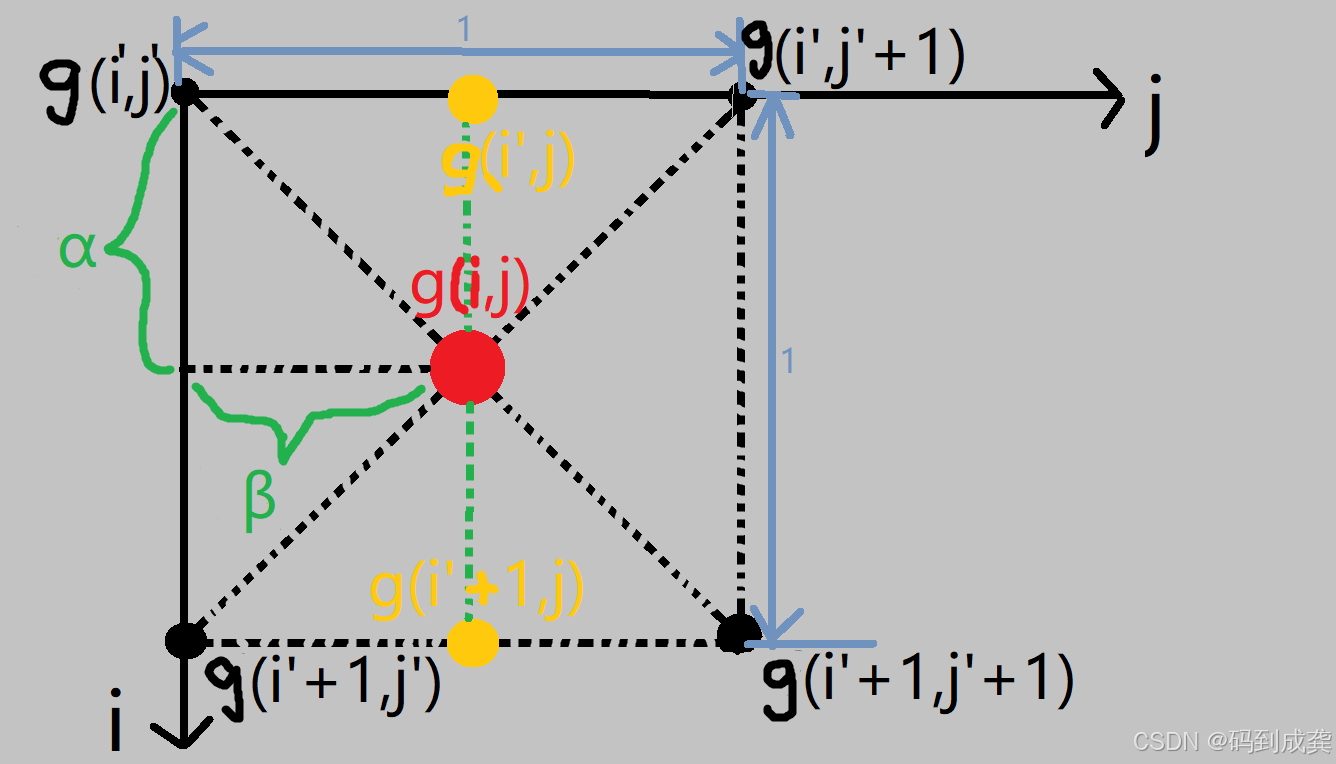
《数字图像处理基础》学习07-图像几何变换之最近邻插值法放大图像
目录 一,概念 二,题目及matlab实现 1,解题思路 2,matlab实现 1)matlab思路 2)完整代码 三,放大图像及matlab实现 一,概念 通过上一篇,我已经学习了使用最邻近插…...

pip安装库时报错(请求超时)
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

XPath表达式详解及其在Web开发中的应用
XPath(XML Path Language)是一种强大的查询语言,用于在XML文档中选择节点。由于HTML可以被视为一种特殊的XML,因此XPath同样适用于HTML文档。XPath允许开发者通过元素的层级结构和属性来选择节点或节点集合,这使得它成…...

Qt中Socket网络编程
文章目录 Qt中Socket网络编程服务器端客户端 Qt中Socket网络编程 这里就拿b站上爱编程的小丙的demo来做总结吧,首先要感谢成功带我入门的人:爱编程的小丙和程序员长风,这两个人是讲Socket编程我听懂的课555,接下来就总结一下Qt中…...

【05】Selenium+Python 两种文件上传方式(AutoIt)
上传文件的两种方式 一、input标签上传文件 可以用send_keys方法直接上传文件 示例代码 input标签上传文件import time from selenium import webdriver from chromedriver_py import binary_path # this will get you the path variable from selenium.webdriver.common.by i…...

Python网络编程
网络编程 Socket(套接字) socket 位于 网络协议中的 数据传输层、 该层 主要 可以通过 UDP 或者 TCP协议 实现 数据的传输 TCP 协议 VS UDP协议 tcp : 是一个 可靠的 ,面向 连接的协议。 数据在网络传输中 是安全的,不易丢失的。 TCP连接 在建立的时候&…...

openssl生成ca证书
常见CA文件夹 1、生成CA钥匙 openssl genrsa -out ./private/cakey.pem 2、生成CA自签名 openssl req -new -x509 -key ./private/cakey.pem -out ./cacert.crt -days 3650 3、生成http服务器私钥 openssl genrsa -out ./data/frontt.project.com.key 2048 4、CA给http服务器…...

Oracle RAC 环境下数据文件误建在本地目录的处理过程
问题描述 在 Oracle RAC 环境中,有时会误将数据文件创建在本地目录,导致其他节点无法访问该数据文件,从而报出 ORA-01157 和 ORA-01110 错误。 问题分析 错误日志 Mon Nov 16 19:02:38 2021 Errors in file /u01/app/oracle/diag/rdbms/orc…...

新质驱动·科东软件受邀出席2024智能网联+低空经济暨第二届湾区汽车T9+N闭门会议
为推进广东省加快发展新质生产力,贯彻落实“百县千镇万村高质量发展工程”,推动韶关市新丰县智能网联新能源汽车、低空经济与数字技术的创新与发展,充分发挥湾区汽车产业链头部企业的带动作用。韶关市指导、珠三角湾区智能网联新能源汽车产业…...

windows11 使用体验记录
好的地方: UI上字体风格貌似更好看了,文件夹增加了多个标签,类似于浏览器既可以打开多个窗口,也可以在同一个窗口中打开多个标签页 不好的地方: 桌面右下角点击日期时间,显示日期,时间呢&…...

202页MES项目需求方案深入解读,学习MES系统设计规划
202页MES项目需求方案深入解读,学习MES系统设计规划 MES项目需求方案旨在实现制造执行、效率提升、精细化管理等多个方面的功能。整体结构分为七大部分,包括制造执行、效率、精细化、品质在线、设备、用户思想和数据互联。制造执行部分关注订单、品质数据…...

前端css实例
前端css实例 一、带条纹的表格 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>条纹样式的表格<…...

YOLO的框架及版本迭代
YOLO(You Only Look Once)是一种非常流行的实时目标检测算法,其特点是将目标检测任务转换为一个回归问题,通过一次前向传播就可以同时完成目标的分类和定位。以下是YOLO框架的整体架构和工作原理: 一、YOLO的基本框架…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
