对力扣77组合优化的剪枝操作的理解
77. 组合
代码随想录放出了这一张图

我乍一看觉得想当然,但是仔细想想,又不知道以下剪枝代码作何解释,因此我想通过这篇文章简要解释一下
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(int n, int k, int startIndex) {if (path.size() == k) {result.push_back(path);return;}for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 剪枝的地方path.push_back(i); // 处理节点backtracking(n, k, i + 1);path.pop_back(); // 回溯,撤销处理的节点}}
public:vector<vector<int>> combine(int n, int k) {backtracking(n, k, 1);return result;}
};for循环里的"i <= n - (k - path.size()) + 1;"就是令人疑惑的地方,我的解释如下:
i是当前取何值,该限制条件就是i在当前所能取的值,既然i能在这取值,我们必须要保证下面的递归嵌套里面的for循环也能取到值(即基于该栈的后面的递归嵌套只能在i之后取值,我们要保证在这之后到n之间有足够的值保证path.size() == k),也就是说当下取值 i 后,所剩下能取的值必须满足path.size() == k这个条件.
因此当下i的可取范围应是能满足后面所有递归都能取值的前提下所能取的范围
在取当下的i值前,path还差k - path.size()个值才能满足path.size() == k,因为在[1,n]取值,那么这最后k - path.size()个值就必须不能超过[n - (k - path.size()) + 1, n],即n的后k - path.size()个值,因为i当前取值超过n - (k - path.size()) + 1后,后面的递归总有i无法取到值.
碎碎念:
泡图书馆也600个小时了,感觉自己的学习效率也慢慢好起来了,也能坚持每天8-10个小时学习了,我想对自己说一句:再接再厉!!未来可期!
相关文章:

对力扣77组合优化的剪枝操作的理解
77. 组合 代码随想录放出了这一张图 我乍一看觉得想当然,但是仔细想想,又不知道以下剪枝代码作何解释,因此我想通过这篇文章简要解释一下 class Solution { private:vector<vector<int>> result;vector<int> path;void backtracking(int n, int k, int sta…...

SpringMVC中的Handler、HandlerMapping、HandlerAdapter
SpringMVC中的Handler、HandlerMapping、HandlerAdapter到底是啥 这东西,虽然说和我们的开发没啥关系,尤其是当你用SpringBoot进行开发时,这些接口离你越来越远了。讲实话,要不是这学期扫一眼学校的课件,我都不知道有这东西,这东西本来就是对使用框架进行开发的开发者隐藏…...

tomcat 8在idea启动控制台乱码
Tomcat 8在IntelliJ IDEA(简称IDEA)启动控制台出现乱码的问题,通常是由于Tomcat的默认编码格式(UTF-8)与IDEA或操作系统的默认编码格式(如GBK)不一致所导致的。以下是一些解决此问题的步骤&…...
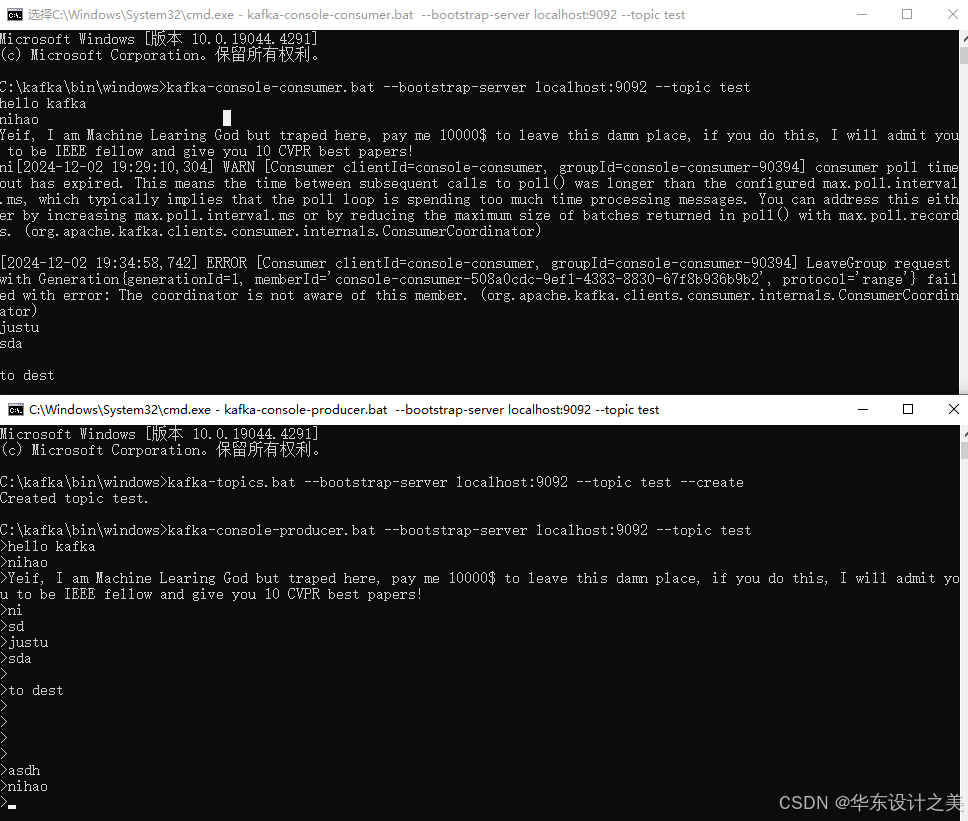
windows下kafka初体验简易demo
这里提供了windows下的java1.8和kafka3.9.0版本汇总,可直接免费下载 【免费】java1.8kafka2.13版本汇总资源-CSDN文库 解压后可以得到一个文件夹 资料汇总内有一个kafka文件资料包.tgz,解压后可得到下述文件夹kafka_2.13-3.9.0,资料汇总内还…...

证明直纹极小曲面是平面或者正螺旋面.
目录 证明直纹极小曲面是平面或者正螺旋面 证明直纹极小曲面是平面或者正螺旋面 证明:设极小直纹面 S S S的参数表示为 r ( u , v ) a ( u ) v c ( u ) . (u,v)\mathbf{a}(u)v\mathbf{c}(u). (u,v)a(u)vc(u).则 r u a ′ v c ′ , r v c , r u ∧ r v a ′ ∧…...

matlab2024a安装
1.开始安装 2.点击安装 3.选择安装密钥 4.接受条款 5.安装密钥 21471-07182-41807-00726-32378-34241-61866-60308-44209-03650-51035-48216-24734-36781-57695-35731-64525-44540-57877-31100-06573-50736-60034-42697-39512-63953 6 7.选择许可证文件 8.找许可证文件 9.选…...

Observability:如何在 Kubernetes pod 中轻松添加应用程序监控
作者:来自 Elastic Jack Shirazi•Sylvain Juge•Alexander Wert Elastic APM K8s Attacher 允许将 Elastic APM 应用程序代理(例如 Elastic APM Java 代理)自动安装到 Kubernetes 集群中运行的应用程序中。该机制使用变异 webhook࿰…...

关于Nginx前后端分离部署spring boot和vue工程以及反向代理的配置说明
最近项目中用到关于Nginx前后端分离部署spring boot和vue工程以及反向代理的配置,总结了一下说明: 1、后端是spring boot工程,端口8000,通过 jar命令启动 nohup java -jar xxx-jsonflow-biz.jar > /usr/local/nohup.out 2>…...

redis渐进式遍历
文章目录 一. 渐进式遍历介绍二. scan命令 一. 渐进式遍历介绍 keys * , 一次性把整个redis中所有的key都获取到, 这个操作比较危险, 可能会阻塞redis服务器 通过渐进式遍历, 就可以做到, 既能够获取到所有的key, 又不会卡死服务器 渐进式遍历, 不是一个命令把所有key都拿到,…...

【C++】数据类型与操作实践:详细解析与优化
博客主页: [小ᶻ☡꙳ᵃⁱᵍᶜ꙳] 本文专栏: C 文章目录 💯前言💯题目一:三个数的倒序输出1.1 题目描述与代码实现代码实现: 1.2 代码解析与细节说明1.3 使用 int 类型的合理性分析1.4 其他数据类型的考虑1.5 代码优…...

C# 集合(Collection)
文章目录 前言一、动态数组(ArrayList)二、哈希表(Hashtable)三、排序列表(SortedList)四、堆栈(Stack)五、队列(Queue)六、点阵列(BitArray&…...

【智能控制】实验,基于MATLAB的模糊推理系统设计,模糊控制系统设计
关注作者了解更多 我的其他CSDN专栏 过程控制系统 工程测试技术 虚拟仪器技术 可编程控制器 工业现场总线 数字图像处理 智能控制 传感器技术 嵌入式系统 复变函数与积分变换 单片机原理 线性代数 大学物理 热工与工程流体力学 数字信号处理 光电融合集成电路…...

前端跳转路由的时候,清掉缓存
清除路由缓存的方法 使用 $router.push() 方法:在跳转路由时,可以通过传递一个包含 replace: true 属性的对象来实现清除路由缓存。例如: this.$router.push({ path: "/new-route", replace: true }); 使用 $router.replace…...

基于 LlamaFactory 的 LoRA 微调模型支持 vllm 批量推理的实现
背景 LlamaFactory 的 LoRA 微调功能非常便捷,微调后的模型,没有直接支持 vllm 推理,故导致推理速度不够快。 LlamaFactory 目前支持通过 VLLM API 进行部署,调用 API 时的响应速度,仍然没有vllm批量推理的速度快。 …...

【赵渝强老师】PostgreSQL的物理存储结构
PostgreSQL在执行initdb的数据库集群初始化时会指定一个目录。该目录通过环境变量$PGDATA来表示。当数据库集群初始化完成后,会在这个目录生成相关的子目录以及一些文件。这些生成的文件就是PostgreSQL的物理存储结构中的文件。如下图所示。 如上图所示,…...

智能探针技术:实现可视、可知、可诊的主动网络运维策略
网络维护的重要性 网络运维是确保网络系统稳定、高效、安全运行的关键活动。在当今这个高度依赖信息技术的时代,网络运维的重要性不仅体现在技术层面,更关乎到企业运营的方方面面。网络运维具有保障网络的稳定性、提升网络运维性能、降低企业运营成本等…...
)
CTF-PWN: 全保护下格式化字符串利用 [第一届“吾杯”网络安全技能大赛 如果能重来] 赛后学习(不会)
通过网盘分享的文件:如果能重来.zip 链接: https://pan.baidu.com/s/1XKIJx32nWVcSpKiWFQGpYA?pwd1111 提取码: 1111 --来自百度网盘超级会员v2的分享漏洞分析 格式化字符串漏洞,在printf(format); __int64 sub_13D7() {char format[56]; // [rsp10h] [rbp-40h]…...

debian 11 虚拟机环境搭建过坑记录
目录 安装过程系统配置修改 sudoers 文件网络配置换源安装桌面mount nfs 挂载安装复制功能tab 无法补全其他安装 软件配置eclipse 配置git 配置老虚拟机硬盘挂载 参考 原来去 debian 官网下载了一个最新的 debian 12,安装后出现包依赖问题,搞了半天&…...

MYSQL 什么是内连接 外连接 左连接 右连接?及适用场景
在 SQL 中,连接(JOIN)是用于组合来自两个或更多表的行的一种方法。根据连接的方式不同,可以分为几种类型的连接:内连接(INNER JOIN)、外连接(OUTER JOIN)、左连接&#x…...

利用Ubuntu批量下载modis图像(New)
由于最近modis原来批量下载的代码不再直接给出,因此,再次梳理如何利用Ubuntu下载modis数据。 之前的下载代码为十分长,现在只给出一部分,需要自己再补充另一部分。之前的为: 感谢郭师兄的指导(https://blo…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
Axure零基础跟我学:展开与收回
亲爱的小伙伴,如有帮助请订阅专栏!跟着老师每课一练,系统学习Axure交互设计课程! Axure产品经理精品视频课https://edu.csdn.net/course/detail/40420 课程主题:Axure菜单展开与收回 课程视频:...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...
