Algorithm:河内之塔
1. 说明
2. 解法
- 每次只能移动一个盘子。
- 不能将较大的盘子放在较小的盘子上。
- 可以使用一个辅助棒(B)。
2.1 算法分析
- 如果只有一个盘子,直接从A移动到C。
- 如果有多个盘子:
2.2 C语言实现
2.3 示例运行
2.4 运行原理
- 将盘1和盘2移到辅助棒B:
- 将盘3移到目标棒C。
- 将盘1和盘2从辅助棒B移到目标棒C:

2.5 注意事项
- 此代码适用于任何正整数的盘子数量,但盘子数量较大时,递归深度可能超过栈的限制。
- 时间复杂度为 O(2^n),因此对大盘子数量的计算效率较低。
3. 附件
3.1 问题的分解特性
- 要把所有盘子从A移动到C,首先需要将除了最大的盘子之外的盘子从A移动到B,然后将最大的盘子从A移动到C,最后将剩下的盘子从B移动到C。
- 这个过程重复进行,直到只剩下一个盘子时,问题变得简单。
3.2 边界条件
- 在“河内之塔”中,当只有一个盘子时(即 n = 1),移动问题非常简单,直接将该盘子从起始棒移动到目标棒。
3.3 递归调用的结构
- 将 n-1 个盘子从起始棒移动到辅助棒。
- 将第 n 个盘子(即最大盘子)从起始棒移动到目标棒。
- 将 n-1 个盘子从辅助棒移动到目标棒。
3.4 数学归纳法的验证
- 当 n = 1 时,移动一个盘子显然是正确的。
- 假设对于 n = k 时,已经正确实现了将 k 个盘子从起始棒移动到目标棒。
- 对于 n = k+1,我们可以将问题分解为两个部分:首先递归地将 k 个盘子从起始棒移动到辅助棒,然后将第 k+1 个盘子(最大盘子)从起始棒移动到目标棒,最后递归地将 k 个盘子从辅助棒移动到目标棒。
3.5 总结
- 问题具有分解特性:大问题可以分解为更小的相同问题。
- 存在明确的基本情况,当问题规模为1时可以直接求解。
- 问题通过递归调用来逐步解决每个子问题,直到最小问题得到解决。
相关文章:

Algorithm:河内之塔
1. 说明 河内之塔(Towers of Hanoi)是法国人 M.Claus(Lucas)于1883年从泰国带至法国的,河内为越战时北越的首都,即现在的胡志明市;1883年法国数学家 Edouard Lucas 曾提及这个故事,据…...

集中管理与实时审计:构建Linux集群(1300台服务器)日志平台的最佳实践
简介 随着企业IT基础设施的不断扩大,Linux服务器的数量也日益增多,传统的单机日志管理方式已无法满足对日志数据集中管理、审计和分析的需求。尤其是在大型集群环境中,如何高效地收集、存储和分析日志成为了一项重要的技术挑战。 背景 在实…...

在Scala中Array不可变的学习
package gjhs114import scala.collection.mutable.ArrayBuffer object Arrray114 {// 不可变数组:Array// def main(args: Array[String]): Unit {1 创建不可变数组// val arr1 Array(1,2,3)//2 访问.数组名(下标)。下标是从0开始到…...

vue3+vite 批量引入组件动态使用
import { ref, reactive, toRaw, markRaw, defineAsyncComponent, onMounted } from vue import type { Component } from vue// vue3vite 批量引入组件动态使用 const modules import.meta.glob<Component>(./details/*.vue) // 明确指定导入的模块类型为Component con…...

设计模式——方法链or流式接口
方法链或流式接口是一种编程模式或设计模式。核心思想是通过返回对象自身的应用,使得可以在一个表达式中连续调用多个方法。 c中实现这种模式 1.基本语法规则 (1)每个可链接的方法都返回对象自身的引用(通常是*this)…...

JAVA OPCUA 服务端开发,客户端连接会话监听和订阅事件监听
前言 关于使用milo开源库,开发opc ua服务器,有网友咨询如何设置服务端如何监听客户端的连接或断开事件,如何监听客户端发起订阅事件的代码实现,于是我完善了这部分的空缺整理整了这篇教程,希望能解决有同样需求,但是遇到困难的网友!因为milo没有官方文档的教程且网上详…...

pytest相关总结
1.pytest -v -s -v将测试用例名称和用例中的输出进行展示,将每条用例脚本的内容逐行进行结果展示; -s 参数是为了显示用例执行层级的打印信息 pytest使用总结笔记 - fengf233 - 博客园 2....

cin/cout的性能优化和缓冲区同步问题
目录 背景导入 问题 1.1ios::sync_with_stdio(false) 1.2为什么要解除C/C IO流同步? 1.3使用场景 2.1cin和cout的绑定关系 2.2为什么要解除绑定关系? 2.3注意事项 背景导入 大家可以先看一下这段背景知识;后面我会谈谈自己的理解; 1.在C中,标准输⼊输出流…...

redisson-spring-data与Spring-Data-Redis的版本关系问题
redisson-spring-boot-starter https://github.com/redisson/redisson/tree/master/redisson-spring-boot-starter https://github.com/redisson/redisson/tree/master/redisson-spring-data#spring-data-redis-integration 将 Redisson 与 Spring Boot 库集成。依赖于Spring…...

Puppeteer代理认证的最佳实践和示例
在现代网络环境中,代理服务器的使用越来越普遍,尤其是在数据抓取、网页自动化测试和网络监控等领域。Puppeteer作为一个流行的Node库,它提供了高级的API来控制Chrome或Chromium浏览器。在某些情况下,我们需要通过代理服务器来执行…...

js 字符串 只显示数字
1. 使用正则表达式的match方法 原理:正则表达式\d用于匹配一个或多个数字。match方法会在字符串中查找与正则表达式匹配的部分,并返回一个包含所有匹配结果的数组。示例代码: let str "abc123def456"; let numbers str.match(/…...

STM32标准库-FLASH
FLASH模仿EEPROM STM32本身没有自带EEPROM,但是自带了FLASH存储器。 STM32F103ZET6自带 1M字节的FLASH空间,和 128K64K的SRAM空间。 STM32F4 的 SPI 功能很强大,SPI 时钟最高可以到 37.5Mhz,支持 DMA,可以配置为 SPI协…...

PowerShell:查找并关闭打开的文件
Get-SmbOpenFile 打开 Windows PowerShell 并运行 Get-SmbOpenFile | Format-List 若要仅显示特定文件共享的连接,请使用 Where-Object 运行 Get-SmbOpenFile。 Get-SmbOpenFile | Where-Object Path -eq "C:\Data\" | Format-List Get-SmbSession 显…...

【AI系统】昇腾异构计算架构 CANN
昇腾异构计算架构 CANN 本文将介绍昇腾 AI 异构计算架构 CANN(Compute Architecture for Neural Networks),这是一套为高性能神经网络计算需求专门设计和优化的架构。CANN 包括硬件层面的达芬奇架构和软件层面的全栈支持,旨在提供…...

STM32 HAL库开发学习3.STM32启动浅析
STM32 HAL库开发学习3.STM32启动浅析 一、STM32启动模式(也称自举模式)1. MSP与PC指针赋值2. F1系列的启动模式:3. F4系列启动模式4. F7系列启动模式5. H7系列启动模式 二、STM32启动过程1. MSP 栈顶地址2. PC值3. Reset_Handler4. 启动文件内…...

FakeLocation 1.3.5 BETA 提示校园跑漏洞修复解决
任务一 作者对此又进行了更新,在本次更新中,我们依旧使用hookvip进行破解 本次的更新,使得包名强制写入更加严重,之前靠一些方法已经无法阻止appconfigs.xml的文件的修改,而且使得验证加强,和云端加强&…...
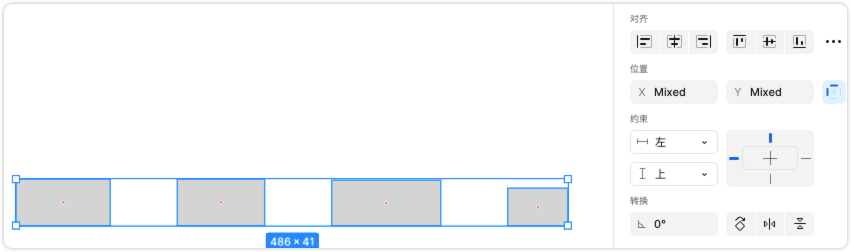
Figma入门-约束与对齐
Figma入门-约束与对齐 前言 在之前的工作中,大家的原型图都是使用 Axure 制作的,印象中 Figma 一直是个专业设计软件。 最近,很多产品朋友告诉我,很多原型图都开始用Figma制作了,并且很多组件都是内置的,…...

腾讯元宝深度搜索AI多线程批量生成TXT原创文章软件
腾讯元宝深度搜索AI多线程批量生成TXT原创文章软件说明: 腾讯元宝深度搜索AI:能够理解用户意图,对搜索结果进行提炼和总结,直接提供用户所需的答案或信息摘要,从而提升用户体验。 腾讯元宝深度搜索AI:通过…...

Git操作学习1
一、一些Linux相关指令 在当前目录下,创建文件并写入内容:echo "这是第一个文件">file1.txt 查看文件的内容: cat file1.txt 会显示:这是第一个文件 修改文件名:mv file.txt file4.txt 把file.txt修改…...

【计算机网络】细说IP
文章目录 概述IP地址的组成IP地址的分类IP地址的作用 分类一、A类IP地址二、B类IP地址三、C类IP地址四、D类IP地址五、E类IP地址 协议报文子网掩码一、定义与功能二、表示方法三、子网掩码与IP地址的关系四、子网掩码的设置与配置五、实例说明 IPv6一、定义与背景二、地址格式与…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...
