【强化学习入门笔记】1.5 贝尔曼最优公式

本系列为学习赵世钰老师的《强化学习的数学原理》所作的学习笔记.
课程视频网址:https://space.bilibili.com/2044042934
1.5.1 定义
1.5.1.1 Contraction mapping theorem (收缩映射定理)
- fixed point(不动点)
如果 x ∗ x^* x∗满足下式, x ∗ x^* x∗称之为fixed point(不动点)
f ( x ∗ ) = x ∗ f\left(x^*\right)=x^* f(x∗)=x∗
- Contraction mapping (收缩映射)
如果一个函数满足下面不等式, 则称这个函数满足Contraction mapping
∥ f ( x 1 ) − f ( x 2 ) ∥ ≤ γ ∥ x 1 − x 2 ∥ γ ∈ ( 0 , 1 ) \left\|f\left(x_1\right)-f\left(x_2\right)\right\| \leq \gamma\left\|x_1-x_2\right\| \\ \gamma \in(0,1) ∥f(x1)−f(x2)∥≤γ∥x1−x2∥γ∈(0,1)
- Contraction mapping theorem (收缩映射定理)
如果函数 f ( x ) f(x) f(x)满足Contraction mapping, 则有Contraction mapping theorem:
- 存在性: 一定存在fixed point, 使其满足 f ( x ∗ ) = x ∗ f\left(x^*\right)=x^* f(x∗)=x∗
- 唯一性: fixed point x ∗ x^* x∗一定是唯一的
- 求解算法: x ∗ x^* x∗可以通过迭代计算得到, 并且迭代会指数收敛
1.5.1.2 贝尔曼最优公式
如果对于所有的状态 S \mathcal{S} S, 策略 π ∗ \pi^* π∗的状态值大于等于其他任何一个策略的状态值, 那么 π ∗ \pi^* π∗称之为 S \mathcal{S} S状态空间中的最优策略:
v π ∗ ( s ) ≥ v π ( s ) for all s ∈ S v_{\pi^*}(s) \geq v_\pi(s) \text { for all } s \in \mathcal{S} vπ∗(s)≥vπ(s) for all s∈S
在贝尔曼公式的基础上, 求解使得状态值 v ( s ) v(s) v(s)最大的策略 π ( s ) \pi(s) π(s)就是贝尔曼最优公式:
v ( s ) = max π ( s ) ∈ Π ( s ) ∑ a ∈ A π ( a ∣ s ) ( ∑ r ∈ R p ( r ∣ s , a ) r + γ ∑ s ′ ∈ S p ( s ′ ∣ s , a ) v ( s ′ ) ) = max π ( s ) ∈ Π ( s ) ∑ a ∈ A π ( a ∣ s ) q ( s , a ) , \begin{aligned}v(s) & =\max _{\pi(s) \in \Pi(s)} \sum_{a \in \mathcal{A}} \pi(a \mid s)\left(\sum_{r \in \mathcal{R}} p(r \mid s, a) r+\gamma \sum_{s^{\prime} \in \mathcal{S}} p\left(s^{\prime} \mid s, a\right) v\left(s^{\prime}\right)\right) \\& =\max _{\pi(s) \in \Pi(s)} \sum_{a \in \mathcal{A}} \pi(a \mid s) q(s, a),\end{aligned} v(s)=π(s)∈Π(s)maxa∈A∑π(a∣s)(r∈R∑p(r∣s,a)r+γs′∈S∑p(s′∣s,a)v(s′))=π(s)∈Π(s)maxa∈A∑π(a∣s)q(s,a),
将贝尔曼最优公式写成矩阵形式:
v = max π ∈ Π ( r π + γ P π v ) v=\max _{\pi \in \Pi}\left(r_\pi+\gamma P_\pi v\right) v=π∈Πmax(rπ+γPπv)
如果将右边的最优化问题, 定义为函数 f ( x ) f(x) f(x):
v = f ( v ) = max π ( r π + γ P π v ) v=f(v)=\max _\pi\left(r_\pi+\gamma P_\pi v\right) v=f(v)=πmax(rπ+γPπv)
书中详细证明了函数符合Contraction mapping, 有兴趣可以看详细证明, 这里我们使用结论即可.
1.5.2 最优解及其特性
1.5.2.1 最优解
Contraction mapping theorem告诉我们:贝尔曼最优公式一定存在唯一解 v ∗ v^* v∗, 并且可以用迭代的方式求解.
当我们有了最优解 v ∗ v^* v∗之后, 就有它对应的最优策略 π ∗ \pi^* π∗:
π ∗ = arg max π ∈ Π ( r π + γ P π v ∗ ) \pi^*=\arg \max _{\pi \in \Pi}\left(r_\pi+\gamma P_\pi v^*\right) π∗=argπ∈Πmax(rπ+γPπv∗)
那么贝尔曼最优公式可以简写成:
v ∗ = r π ∗ + γ P π ∗ v ∗ v^*=r_{\pi^*}+\gamma P_{\pi^*} v^* v∗=rπ∗+γPπ∗v∗
我们可以发现, 这就是一个贝尔曼公式. 只不过他的参数是最优策略 π ∗ \pi^* π∗, 也就是说贝尔曼最优公式是贝尔曼公式在最优策略下的一个特殊形式.
v ∗ = v π ∗ ≥ v π v^*=v_{\pi^*} \geq v_\pi v∗=vπ∗≥vπ, 书中同样详细证明了为什么 v ∗ v^* v∗和 π ∗ \pi^* π∗是最优的.
1.5.2.2 Greedy optimal policy(贪婪最优定理)
最优策略 π ∗ \pi^* π∗的Greedy optimal policy(贪婪最优定理), 对于任何 s ∈ S s ∈ S s∈S,贝尔曼最优公式的最优解唯一, 且是确定性贪婪策略:
π ∗ ( a ∣ s ) = { 1 , a = a ∗ ( s ) , 0 , a ≠ a ∗ ( s ) , \pi^*(a \mid s)= \begin{cases}1, & a=a^*(s), \\ 0, & a \neq a^*(s),\end{cases} π∗(a∣s)={1,0,a=a∗(s),a=a∗(s),
之所以称之为贪婪, 是因为只有最优动作的概率是1, 其他动作概率都是0. 但是仍然有以下两个性质需要注意:
- π ∗ \pi^* π∗不唯一: 虽然最优解 v ∗ v^* v∗的值是唯一的, 但是最优策略不唯一. 也就是说, 可能有多个策略的状态值都是最优.
- π ∗ \pi^* π∗可能是随机策略: 虽然Greedy optimal policy告诉我们, 一定存在一个确定性的策略 π ∗ \pi^* π∗; 但是因为 π ∗ \pi^* π∗不唯一, 其他的 π ∗ \pi^* π∗可能是随机策略.

这个例子可以说明上面的两个特性: 两个策略的状态值都是最优, 那么它们都是最优策略; 并且左边是确定策略, 右边是随机策略.
1.5.3 例子
我们重新回顾贝尔曼最优公式:
v ( s ) = max π ( s ) ∈ Π ( s ) ∑ a ∈ A π ( a ∣ s ) ( ∑ r ∈ R p ( r ∣ s , a ) r + γ ∑ s ′ ∈ S p ( s ′ ∣ s , a ) v ( s ′ ) ) , s ∈ S . v(s)=\max _{\pi(s) \in \Pi(s)} \sum_{a \in \mathcal{A}} \pi(a \mid s)\left(\sum_{r \in \mathcal{R}} p(r \mid s, a) r+\gamma \sum_{s^{\prime} \in \mathcal{S}} p\left(s^{\prime} \mid s, a\right) v\left(s^{\prime}\right)\right), \quad s \in \mathcal{S} . v(s)=π(s)∈Π(s)maxa∈A∑π(a∣s)(r∈R∑p(r∣s,a)r+γs′∈S∑p(s′∣s,a)v(s′)),s∈S.
- 求解目标: 状态值 v ( s ) v(s) v(s), 策略 π ( s ) \pi(s) π(s)
- 参数 r , γ r,\gamma r,γ: 通过改变奖励设计和折扣率, 可以改变最优解
1.5.3.1 γ \gamma γ的影响
举个例子说明参数的影响,在这样参数设置时:
- 抵达禁止格或边界的奖励是-1: r boundary = r forbidden = − 1 r_{\text {boundary }}=r_{\text {forbidden }}=-1 rboundary =rforbidden =−1
- 抵达终点的奖励是1: r target = 1 r_{\text {target }}=1 rtarget =1
- γ = 0.9 \gamma=0.9 γ=0.9
- 其他行为奖励是0
它的最优策略和最优状态值如下图所示, 它会倾向于穿过禁止格, 抵达终点:

当我们把 γ = 0.5 \gamma=0.5 γ=0.5时, 最优策略则倾向于绕过禁止格, 抵达终点:

当我们把 γ = 0 \gamma=0 γ=0时, 最优策略则几乎放弃抵达终点, 倾向于脱离禁止格后原地不动, 因为它只考虑了眼前的即时动作奖励:

这几个例子说明了 γ \gamma γ代表奖励设计的远视程度: γ \gamma γ越大说明越鼓励长远的收益; γ \gamma γ越小说明越鼓励眼前的收益;
不过需要说明的是, 只要 γ \gamma γ不等于1, 远期收益都会逐渐衰减. 我们可以看return的公式:
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + … G_t =R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\ldots Gt=Rt+1+γRt+2+γ2Rt+3+…
因为 0 ≤ γ ≤ 1 0\leq \gamma \leq1 0≤γ≤1, 越远期的奖励折扣率越小, 它自然的就会使得远期收益逐渐衰减.
1.5.3.2 r r r的影响
如果我们非常不希望策略进入禁止格, 那么我们可以将禁止格惩罚设置为-10或者是更小的值, 来惩罚对应的动作.
但是显而易见的是: 如果整体性的放大奖励, 比如将终点奖励也设置为10, 结果不会有任何变化.
推荐阅读
- 端到端理论与实战
- 动手学轨迹预测
- 动手学运动规划
- 动手学行为决策
- 强化学习入门笔记

相关文章:

【强化学习入门笔记】1.5 贝尔曼最优公式
本系列为学习赵世钰老师的《强化学习的数学原理》所作的学习笔记. 课程视频网址:https://space.bilibili.com/2044042934 1.5.1 定义 1.5.1.1 Contraction mapping theorem (收缩映射定理) fixed point(不动点) 如果 x ∗ x^* x∗满足下式, x ∗ x^* x∗称之为…...

编码问题技术探讨:IDE全局GBK与项目UTF-8引发的中文乱码
在软件开发过程中,编码问题一直是开发者们需要面对和解决的难题之一。尤其是在使用IDE(集成开发环境)时,如果全局编码设置与项目编码设置不一致,往往会导致中文乱码的问题。本文将深入探讨这一问题的背景、示例以及解决…...

SpringBoot两天
SpringBoot讲义 什么是SpringBoot? Spring Boot是由Pivotal团队提供的全新框架,其设计目的是用来简化新Spring应用的初始搭建以及开发过程。该框架使用了特定的方式来进行配置,从而使开发人员不再需要定义样板化的配置。通过这种方式…...

自动化立体仓库项目任务调度系统中任务流程可视化实现
在运维自动化平台中,任务系统无疑是最核心的组成部分之一。它承担着所有打包编译、项目上线、日常维护等运维任务的执行。通过任务系统,我们能够灵活地构建满足不同需求的自定义任务流。早期的任务流后端采用了类似列表的存储结构,根据任务流内子任务的排序依次执行,尽管通…...

计算机毕业设计hadoop+spark民宿推荐系统 民宿数据分析可视化大屏 民宿爬虫 民宿大数据 知识图谱 机器学习 大数据毕业设计
温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 作者简介:Java领…...

Java中OGNL表达式语言的使用
文章目录 OGNL 介绍OGNL 使用场景- ognl- 主要功能- 注意事项- Ognl类的主要方法- 设置值- 获取值- 使用示例 - MybatisJava原生表达式的使用 - Fastjson- JSONPath类的主要方法- 主要功能- JSONPath的优势- 使用示例 Spring不选择OGNL的原因 OGNL 介绍 OGNL(Objec…...

[HCTF 2018]WarmUp-滑稽
启动场景打开链接,出现一下图片 F12查看代码出现一个注释,应该在这个文件中, 进入到该页面,出现一段代码 <?phphighlight_file(__FILE__);class emmm{public static function checkFile(&$page){$whitelist ["sourc…...

JAVAWeb——maven、SpringBoot、HTTP、Tomcat
目录 1.maven a.概述 b.作用 c.仓库 b.坐标 c.依赖管理 2.SpringBoot 3.HTTP a.概述 b.请求协议 c.响应协议 d.协议解析 4.Tomcat a.Web服务器 b.Tomcat c.SpringBoot与Tomcat关系 1.maven a.概述 Maven是apache旗下的一个开源项目,是一款用于管理…...

【C++】—— set 与 multiset
【C】—— map 与 set 1 序列式容器和关联式容器2 set 系列的使用2.1 set 和 multiset 参考文档2.2 set 类的介绍2.3 set 的迭代器和构造2.4 set的增删查2.4.1 insert2.4.2 find 与 erase2.4.3 count 2.5 lower_bound 与 upper_bound2.6 multiset 与 set 的差异2.6.1 不再去重2…...

蓝桥杯-扫雷
这题不难,就是麻烦一点,这里暴力求解了直接 题目链接: 扫雷 AC代码: import java.util.Scanner; // 1:无需package // 2: 类名必须Main, 不可修改public class Main {public static void main(String[] args) {Scanner scan ne…...

黑马JavaWeb-day06、07、08(SQL部分) _
文章目录 MYSQL概述数据模型SQL简介SQL分类 DDL数据库操作表操作 DML增(INSERT)改(UPDATE)删(DELETE) DQL基本查询条件查询(where)分组查询(group by)排序查询…...

三十五:Wireshark的捕获过滤器
Wireshark 是一个广泛使用的网络协议分析工具,主要用于捕获和分析网络流量。它支持丰富的协议分析,并提供了多种过滤方式,以便用户在大量数据中精确地找到自己关注的内容。在Wireshark中,过滤器可以分为两类:捕获过滤器…...
)
第9章 大模型的有害性(上)
9.1 引言 本章将探讨大型语言模型(LLMs)可能带来的有害性,重点讨论以下几个方面: 性能差异社会偏见和刻板印象 在后续内容中,还会涉及其他层面的危害,如有害信息、虚假信息、隐私和安全风险、版权问题、…...

遗传算法与深度学习实战(26)——编码卷积神经网络架构
遗传算法与深度学习实战(26)——编码卷积神经网络架构 0. 前言1. EvoCNN 原理1.1 工作原理1.2 基因编码 2. 编码卷积神经网络架构小结系列链接 0. 前言 我们已经学习了如何构建卷积神经网络 (Convolutional Neural Network, CNN),在本节中&a…...

Linux无线网络配置工具:iwconfig vs iw
在Linux系统中,无线网络配置和管理是网络管理员和开发者的常见任务。本文将详细介绍两个常用的无线网络配置命令行工具:iwconfig 和 iw,并对比它们之间的区别,帮助您更好地选择合适的工具进行无线网络配置。 一、iwconfig 简介 …...

RabbitMQ介绍及安装
文章目录 一. MQ二. RabbitMQ三. RabbitMQ作用四. MQ产品对比五. 安装RabbitMQ1. 安装erlang2. 安装rabbitMQ3. 安装RabbitMQ管理界⾯4. 启动服务5. 访问界面6. 添加管理员用户7. 重新登录 一. MQ MQ( Message queue ), 从字⾯意思上看, 本质是个队列, FIFO 先⼊先出ÿ…...

借助 AI 工具,共享旅游-卡-项目助力年底增收攻略
年底了,大量的商家都在开始筹备搞活动,接下来的双十二、元旦、春节、开门红、寒假,各种活动,目的就是为了拉动新客户。 距离过年还有56 天,如何破局? 1、销售渠道 针对旅游卡项目,主要销售渠道…...

Docker Compose 和 Kubernetes 之间的区别?
一、简介🎀 1.1 Docker Compose Docker Compose 是 Docker 官方的开源项目,负责实现对 Docker 容器集群的快速编排,可以管理多个 Docker 容器组成一个应用。你只需定义一个 YAML 格式的配置文件 docker-compose.yml ,即可创建并…...

node.js常用的模块和中间件?
Node.js常用的模块和中间件包括以下几种: Express:Express是一个灵活的Node.js web应用框架,提供了丰富的API来处理HTTP请求和响应。它支持中间件系统,可以轻松地添加各种功能,如路由、模板引擎、静态文件服务…...

Llama模型分布式训练(微调)
1 常见大模型 1.1 参数量对照表 模型参数量发布时间训练的显存需求VGG-19143.68M2014~5 GB(单 224x224 图像,batch_size32)ResNet-15260.19M2015~7 GB(单 224x224 图像,batch_size32)GPT-2 117M117M2019~…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
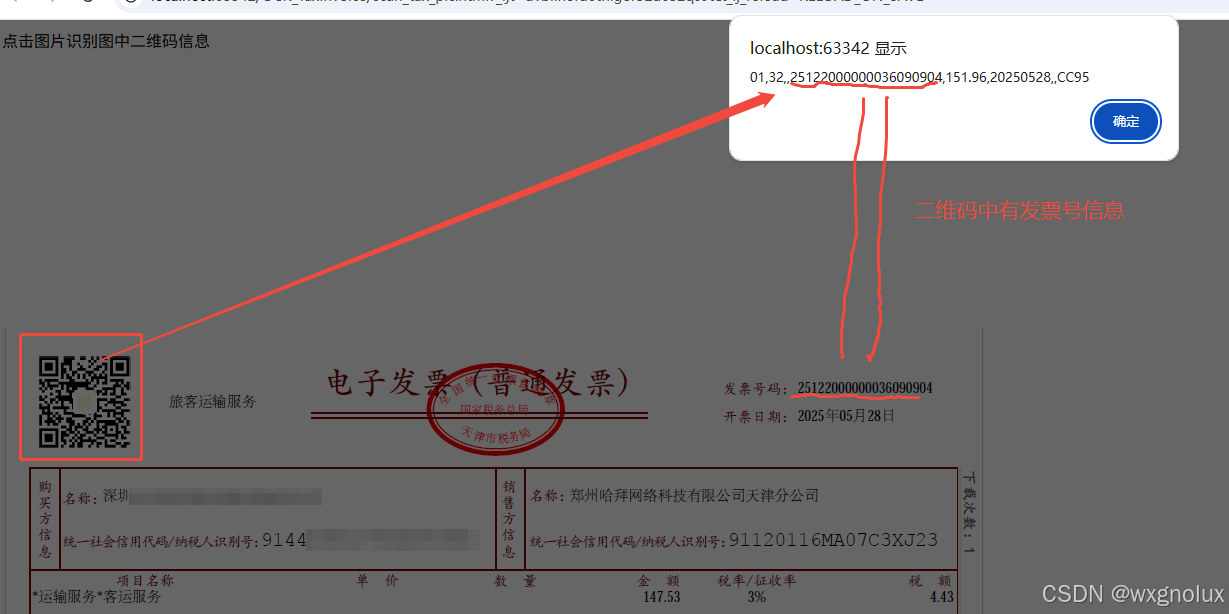
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...
