Lua面向对象实现
Lua中的面向对象是通过表(table)来模拟类实现的,通过setmetatable(table,metatable)方法,将一个表设置为当前表的元表,之后在调用当前表没有的方法或者键时,会再查询元表中的方法和键,以此来实现面向对象。
至于元表和元方法的使用可以看我的这篇文章:
Lua元表和元方法的使用-CSDN博客
一个例子来说明实现:
有一家三口,爸爸是工程师,妈妈是老师,孩子是学生,都会跑步,但是他们从事不同的工作。
实现封装:
local people = {}function people:new ()local t = {}setmetatable(t,self);self.__index = self;return t
endfunction people:talk()print("I'm a person")
endfunction people:running()print("I can run")
end实现继承:
local engineer = people:new();local teacher = people:new();local student = people:new();engineer.running();teacher.running();student.running();输出:

实现多态:
local engineer = people:new();function engineer:talk()print("I'm an engineer")
endlocal teacher = people:new();function teacher:talk()print("I am a teacher")
endlocal student = people:new();function student:talk()print("I am a student")
endengineer.talk();teacher.talk();student.talk();输出:

参考书籍与链接:
《Lua程序设计》
《Cocos2d-x游戏开发:手把手教你Lua语言的编程方法》
掌握 Lua 脚本语言 (pikuma.com)
Creating A Toggle Switch In Wix Studio (youtube.com)
相关文章:

Lua面向对象实现
Lua中的面向对象是通过表(table)来模拟类实现的,通过setmetatable(table,metatable)方法,将一个表设置为当前表的元表,之后在调用当前表没有的方法或者键时,会再查询元表中的方法和键,以此来实现…...

OpenCV的圆形检测HoughCircles
HoughCircles 函数是 OpenCV 库中用于在灰度图像中检测圆的函数,它基于霍夫变换(Hough Transform)的一种变体——梯度霍夫变换(HOUGH_GRADIENT)函数原型如下: void HoughCircles( InputArray image, OutputArray circles,int method, double dp, double minDist,double …...

iOS视图控制器的生命周期及各阶段的作用
iOS视图控制器(UIViewController)的生命周期是指从它被创建到最终被销毁的过程中所经历的一系列阶段。每个阶段都有其特定的作用和执行时机,这些阶段和作用对于开发高效、稳定的iOS应用至关重要。以下是iOS视图控制器的生命周期及其各个阶段的…...

四轮阿克曼(前轮转向、后轮驱动)车子仿真控制
目录 写在前面的话调用 libgazebo_ros_ackermann_drive.so 插件属性介绍补充 steering_wheel_joint 配置键盘控制命令 结果演示 写在前面的话 这里增加一个四轮阿克曼(前轮转向、后轮驱动)车子仿真控制的版本,使用的事gazebo的插件 参考资料…...

Blender均匀放缩模型
解决办法: 首先选中模型,按下“s”键,如下图所示,此时模型根据鼠标的移动放缩 或者在按下“s”后输入数值,再按回车键Enter,模型会根据你该数值进行均匀放缩 指定放大2倍结果——...

Python基于 Opencv+wxPython 的人脸识别上课考勤系统,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...

【AI工具】强大的AI编辑器Cursor详细使用教程
目录 一、下载安装与注册 二、内置模型与配置 三、常用快捷键 四、项目开发与问答 五、注意事项与技巧 参考资料 近日,由四名麻省理工学院(MIT)本科生共同创立的Anysphere公司宣布,其开发的AI代码编辑器Cursor在成立短短两年…...

DApp开发与APP开发的五大区别
随着比特币与区块链技术的不断发展,DApp应用会逐渐成为主流。与APPAPP相比,DApp有许多不同之处,尤其是在架构、数据存储、用户隐私等方面。本文将通过五大关键点,深入探讨DApp开发与APP开发之间的主要区别。 1. 后端架构ÿ…...

哪款云手机适合多开?常用云手机功能对比
在全球化和数字化时代,云手机以其独特的灵活性和高效性,成为多账号运营和数字营销的热门工具。云手机能够解决传统设备管理的诸多痛点,例如账号关联、硬件成本高等问题。本文将为您推荐多款优质云手机品牌,帮助您选择最适合的工具…...
)
Python几种常用数据结构(重制版)
一、列表 [List] 定义:有序可重复的数据集合。示例:my_list [element1, element2, element3]增加元素方法: append():在列表末尾增加单个元素(列表特有方法),例如 my_list.append(element)。e…...
)
C++ 游戏开发:开启游戏世界的编程之旅(2)
三、游戏输入处理 (一)键盘输入处理 在游戏中,玩家通过键盘输入来控制角色的行动。我们需要在游戏循环中不断检测键盘事件,并根据不同的按键按下或松开状态来执行相应的操作。例如,在 SDL 中,可以这样处理…...

用 Python 做数据分析需要掌握哪些基础?
用 Python 做数据分析,需要掌握以下几个基础方面: 1. Python 编程基础 语法基础:变量、数据类型(如字符串、整数、浮点数、布尔值)、条件语句(if-else)、循环(for、while࿰…...

UE5 像素流进行内网https证书创建
确定证书需求 内网 HTTPS 通信通常需要以下内容: 自签名证书(适用于内网环境,不需要通过公开的证书颁发机构 CA) 或者通过内部的企业 CA 签发的证书(更安全)。 生成自签名证书 使用工具(如 Ope…...

Envoy-istio
最近研究envoy-istio,发现这个博客,觉得很不错,这里记录一下 envoy-istio介绍 envoy-istio - 随笔分类 - yaowx - 博客园 envoy部分七:envoy的http流量管理基础 envoy部分六:envoy的集群管理 envoy部分五ÿ…...

CTF-PWN: WEB_and_PWN [第一届“吾杯”网络安全技能大赛 Calculator] 赛后学习(不会)
附件 calculate.html <!DOCTYPE html> <html lang"en"> <head><!-- 设置字符编码为 UTF-8,支持多语言字符集 --><meta charset"UTF-8"><!-- 设置响应式视图,确保页面在不同设备上自适应显示 --&…...

【数据结构与算法】排序算法(上)——插入排序与选择排序
文章目录 一、常见的排序算法二、插入排序2.1、直接插入排序2.2、希尔排序( 缩小增量排序 ) 三、选择排序3.1、直接选择排序3.2、堆排序3.2.1、堆排序的代码实现 一、常见的排序算法 常见排序算法中有四大排序算法,第一是插入排序,二是选择排序ÿ…...

Linux操作系统性能优化
Linux操作系统性能优化 1. TCP连接出现大量ESTABLISHED连接解决方法 1. TCP连接出现大量ESTABLISHED连接解决方法 TCP协议规定,对于已经建立的连接,网络双方要进行四次握手才能成功断开连接,如果缺少了其中某个步骤,将会使连接处于…...

iOS与Windows间传文件
想用数据线从 windows 手提电脑传文件入 iPhone,有点迂回。 参考 [1],要在 windows 装 Apple Devices。装完、打开、插线之后会检测到手机,界面: 点左侧栏「文件」,不是就直接可以传,而是要通过某个应用传…...

在数据库设计中同步冗余字段的思考与实践
目录 前言1. 冗余字段设计的背景与场景1.1 场景描述1.2 冗余字段的必要性 2. 冗余字段设计的优点2.1 提高查询效率2.2 简化应用逻辑 3. 冗余字段设计的缺点与挑战3.1 数据不一致问题3.2 更新开销增加3.3 数据冗余占用存储空间 4. 如何同步更新冗余字段4.1 手动更新方式4.2 使用…...

Qt 带数据库功能的项目部署之后,数据库无法打开问题解决方法
前言:最近项目添加了sqlite数据库功能,在qtcreator直接运行时,打开数据库正常,但是部署之后,发现数据库打开会失败,提示“driver not loaded”错误,后来发现是因为sqldrivers文件夹目录不对导致…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...
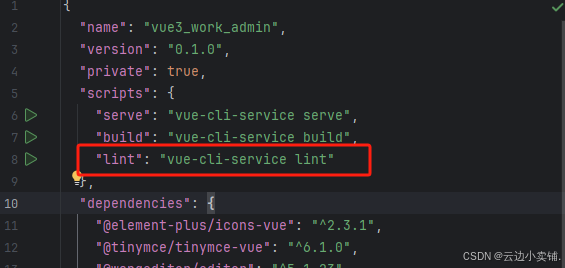
运行vue项目报错 errors and 0 warnings potentially fixable with the `--fix` option.
报错 找到package.json文件 找到这个修改成 "lint": "eslint --fix --ext .js,.vue src" 为elsint有配置结尾换行符,最后运行:npm run lint --fix...

(12)-Fiddler抓包-Fiddler设置IOS手机抓包
1.简介 Fiddler不但能截获各种浏览器发出的 HTTP 请求,也可以截获各种智能手机发出的HTTP/ HTTPS 请求。 Fiddler 能捕获Android 和 Windows Phone 等设备发出的 HTTP/HTTPS 请求。同理也可以截获iOS设备发出的请求,比如 iPhone、iPad 和 MacBook 等苹…...
)
Android多媒体——音/视频数据播放(十八)
在媒体数据完成解码并准备好之后,播放流程便进入了最终的呈现阶段。为了确保音视频内容能够顺利输出,系统需要首先对相应的播放设备进行初始化。只有在设备初始化成功后,才能真正开始音视频的同步渲染与播放。这一过程不仅影响播放的启动速度,也直接关系到播放的稳定性和用…...
