MATLAB 遗传算法

✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。
🍎个人主页:小嗷犬的个人主页
🍊个人网站:小嗷犬的技术小站
🥭个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。
本文目录
- 遗传算法
- MATLAB 实现遗传算法
遗传算法
遗传算法是一种模拟自然界生物进化机制的优化算法,它通过模拟自然选择、交叉和变异等操作来寻找问题的最优解。
遗传算法通常包括以下步骤:
- 定义问题的目标函数和约束条件,以及变量的编码方式。
- 生成初始种群,即一组随机的可行解。
- 计算每个个体的适应度值,即目标函数的值。
- 选择操作,根据适应度值选择一部分个体进入下一代。
- 交叉操作,对选中的个体进行染色体的交换,产生新的个体。
- 变异操作,对某些个体的某些基因进行随机改变,增加种群的多样性。
- 重复3-6步,直到满足终止条件,如达到最大迭代次数或适应度值达到预设阈值。
- 输出最优解或最优解集。
MATLAB 实现遗传算法
MATLAB 中的遗传算法函数为 ga,其基本语法为:
[x,fval] = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon)
其中,fun 为目标函数,nvars 为变量个数,A 为不等式约束系数矩阵,b 为不等式约束右端项,Aeq 为等式约束系数矩阵,beq 为等式约束右端项,lb 为变量下界,ub 为变量上界,nonlcon 为非线性约束函数,intcon 为整数变量的下标。
该函数可以求解线性规划、整数规划、非线性规划、混合整数规划等各种优化问题。
例1
求解以下非线性规划问题:
minf(x)=x12+x22+x32+8\begin{equation} \min \quad f(x)=x_{1}^2+x_{2}^2+x_{3}^2+8 \end{equation} minf(x)=x12+x22+x32+8
s.t. {x12−x2+x32≥0x1+x22+x33≤20−x1−x22+2=0x2+2x32=3x1,x2,x3≥0\begin{equation} \text { s.t. } \left\{ \begin{array}{c} x_{1}^2-x_{2}+x_{3}^2 \geq 0 \\ x_{1}+x_{2}^2+x_{3}^3 \leq 20 \\ -x_{1}-x_{2}^2+2 = 0 \\ x_{2}+2x_{3}^2 = 3 \\ x_{1}, x_{2}, x_{3} \geq 0 \end{array} \right. \end{equation} s.t. ⎩⎨⎧x12−x2+x32≥0x1+x22+x33≤20−x1−x22+2=0x2+2x32=3x1,x2,x3≥0
解
转换为标准形式:
minf(x)=x12+x22+x32+8\begin{equation} \min \quad f(x)=x_{1}^2+x_{2}^2+x_{3}^2+8 \end{equation} minf(x)=x12+x22+x32+8
s.t. {−x12+x2−x32≤0x1+x22+x33−20≤0x1+x22−2=0x2+2x32−3=0x1,x2,x3≥0\begin{equation} \text { s.t. } \left\{ \begin{array}{c} -x_{1}^2+x_{2}-x_{3}^2 \leq 0 \\ x_{1}+x_{2}^2+x_{3}^3-20 \leq 0 \\ x_{1}+x_{2}^2-2 = 0 \\ x_{2}+2x_{3}^2-3 = 0 \\ x_{1}, x_{2}, x_{3} \geq 0 \end{array} \right. \end{equation} s.t. ⎩⎨⎧−x12+x2−x32≤0x1+x22+x33−20≤0x1+x22−2=0x2+2x32−3=0x1,x2,x3≥0
定义目标函数:
function f = objfun(x)f = x(1)^2 + x(2)^2 + x(3)^2 + 8;
end
定义非线性约束函数:
function [c,ceq] = nonlcon(x)c = [-x(1)^2 + x(2) - x(3)^2; x(1) + x(2)^2 + x(3)^3 - 20];ceq = [x(1) + x(2)^2 - 2; x(2) + 2*x(3)^2 - 3];
end
代码求解:
[x,fval] = ga(@objfun,3,[],[],[],[],[0,0,0],[],@nonlcon)
输出结果:
x =0.5516 1.2035 0.9477fval =10.6508
例2
求解以下整数规划问题:
maxZ=4x1+3y1+5y2\begin{equation} \max \quad Z=4x_{1}+3y_{1}+5y_{2} \end{equation} maxZ=4x1+3y1+5y2
s.t. {y1,y2are integers2x1+y1+3y2≤36x1+y1≥8x1+y2≥10x1+y1−y2=4x1,y1,y2≥0\begin{equation} \text { s.t. } \left\{ \begin{array}{c} y_{1},y_{2} \text{ are integers} \\ 2 x_{1}+y_{1}+3y_{2} \leq 36 \\ x_{1}+y_{1} \geq 8 \\ x_{1}+y_{2} \geq 10 \\ x_{1}+y_{1}-y_{2} = 4 \\ x_{1}, y_{1}, y_{2} \geq 0 \end{array} \right. \end{equation} s.t. ⎩⎨⎧y1,y2 are integers2x1+y1+3y2≤36x1+y1≥8x1+y2≥10x1+y1−y2=4x1,y1,y2≥0
解
转换为标准形式:
min−Z=−4x1−3y1−5y2\begin{equation} \min \quad -Z=-4x_{1}-3y_{1}-5y_{2} \end{equation} min−Z=−4x1−3y1−5y2
s.t. {y1,y2are integers2x1+y1+3y2≤36−x1−y1≤−8−x1−y2≤−10x1+y1−y2=4x1,y1,y2≥0\begin{equation} \text { s.t. } \left\{ \begin{array}{c} y_{1},y_{2} \text{ are integers} \\ 2x_{1}+y_{1}+3y_{2} \leq 36 \\ -x_{1}-y_{1} \leq -8 \\ -x_{1}-y_{2} \leq -10 \\ x_{1}+y_{1}-y_{2} = 4 \\ x_{1}, y_{1}, y_{2} \geq 0 \end{array} \right. \end{equation} s.t. ⎩⎨⎧y1,y2 are integers2x1+y1+3y2≤36−x1−y1≤−8−x1−y2≤−10x1+y1−y2=4x1,y1,y2≥0
代码求解:
fun = @(x) -4*x(1) - 3*x(2) - 5*x(3);
A = [2, 1, 3; -1, -1, 0; -1, 0, -1];
b = [36; -8; -10];
Aeq = [1, 1, -1];
beq = 4;
lb = [0, 0, 0];
ub = [];
intcon = [2, 3];
[x,fval] = ga(fun,3,A,b,Aeq,beq,lb,ub,[],intcon);
fval = -fval;
输出结果:
x =4.0000 7.0000 7.0000fval =72.0000
相关文章:

MATLAB 遗传算法
✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。 🍎个人主页:小嗷犬的个人主页 🍊个人网站:小嗷犬的技术小站 🥭个人信条:为天地立心&…...

探讨 Java 中 valueOf 和 parseInt 的区别
前言 在编程中,遇到类型转换,好像会经常用到 parseInt 和 valueOf,当然这里只拿 Integer 类型进行陈述,其他类型也是雷同的; 想必有读者也跟我一样,经常交叉使用这两个方法,但却不知道这两者到…...
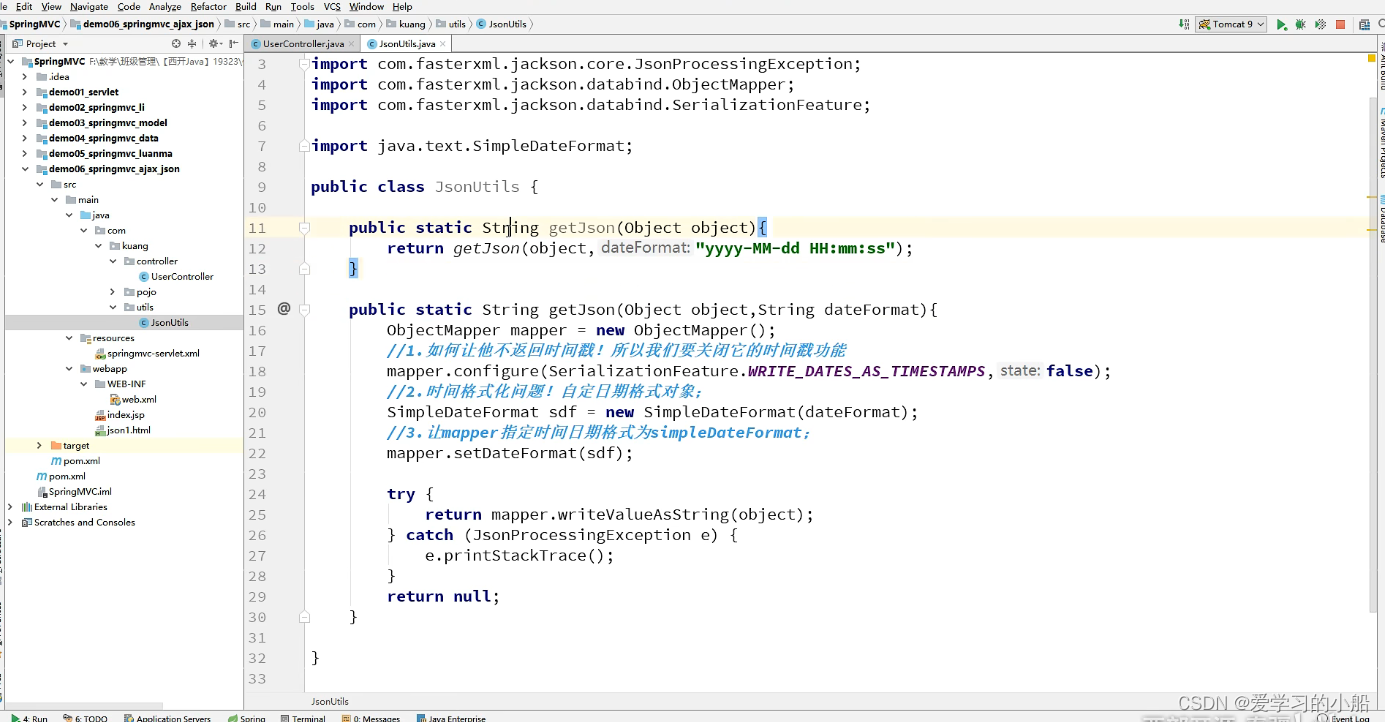
JSON学习笔记
♥课程链接:【狂神说Java】一小时掌握JSON_哔哩哔哩_bilibili配套的当然还要学习ajax不管是前端后端,感觉这部分内容是必须的,不然真的做项目的时候云里雾里。总体json的内容不多,具体就:1. 列表、对象等语法格式2. js…...
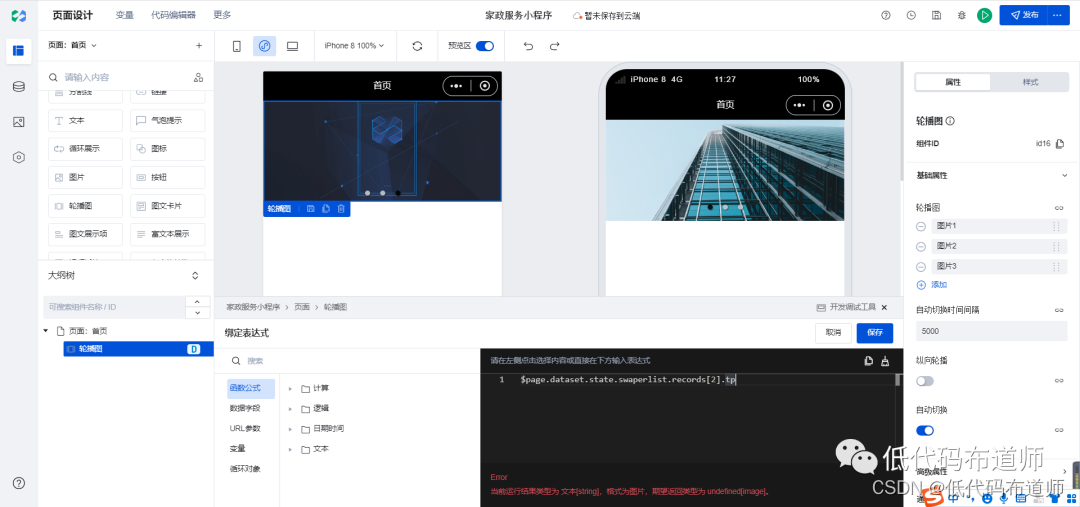
家政服务小程序实战教程07-轮播图组件
小程序中首页一般显示轮播图的功能,点击轮播图会跳转到具体的一篇文章或者是产品,本篇我们就介绍一下轮播图功能的开发 01 设计数据源 我们轮播图组件需要两个字段,一个是展示的图片,一个是跳转页面传入的参数。打开数据源&…...

MySQL之索引创建、删除、唯一索引、普通索引、及命名规则、注意事项
一、MySQL 索引 定义 索引是一个数据结构,用于加速数据库表中数据的查询。索引存储了一些数据表中的列值,以及这些列值在数据表中的位置,这样就可以通过索引来快速查找到数据表中的某一行数据。 MySQL 支持多种索引类型,包括普通…...

【C++设计模式】学习笔记(3):策略模式 Strategy
目录 简介动机(Motivation)模式定义结构(Structure)要点总结笔记结语简介 Hello! 非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~ ଘ(੭ˊᵕˋ)੭ 昵称:海轰 标签:程序猿|C++选手|学生 简介:因C语言结识编程,随后转入计算机专业,获得过国家奖学金…...
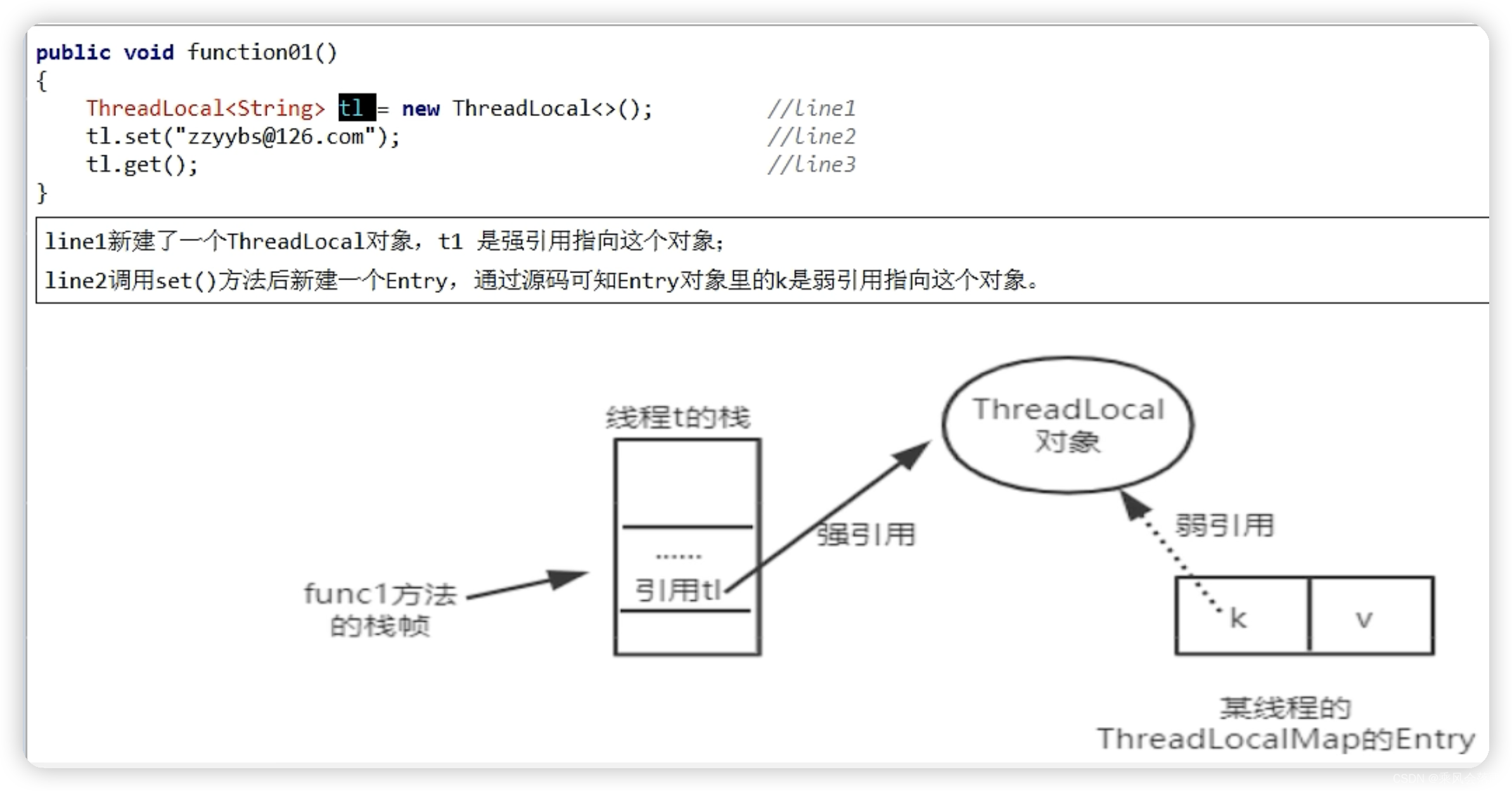
Java——聊聊JUC中的ThreadLocal
文章目录: 1.什么是ThreadLocal? 1.1 api介绍 1.2 最简单的案例认识ThreadLocal 1.3 线程池结合ThreadLocal案例 2.Thread &ThreadLocal & ThreadLocalMap 3.ThreadLocal内存泄漏问题 3.1 四大引用之强引用 3.2 四大引用之软引用 3.3 四…...
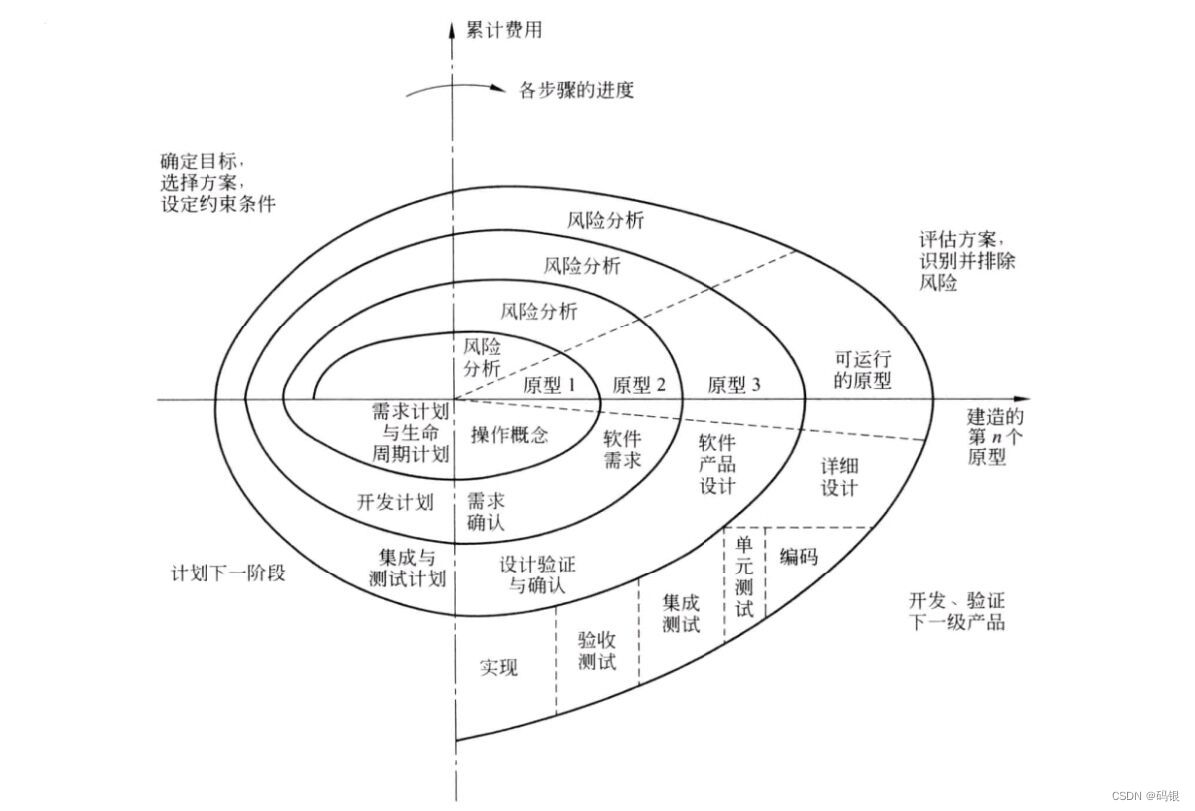
软件工程(4)--螺旋模型
前言 这是基于我所学习的软件工程课程总结的第四篇文章。 在软件开发过程中必须及时识别和分析风险,并且采取适当措施以消除或减少风险的危害。构建原型是一种能使某些类型的风险降至最低的方法。为了降低交付给用户的产品不能满足用户需要的风险,一种行…...

图解LeetCode——剑指 Offer 50. 第一个只出现一次的字符
一、题目 在字符串 s 中找出第一个只出现一次的字符。如果没有,返回一个单空格。 s 只包含小写字母。 二、示例 2.1> 示例 1: 【输入】s "abaccdeff" 【输出】b 2.2> 示例 2: 【输入】s "" 【输出】 限制: 0 < s 的…...

《HTML 5与CSS 3核心技法》读书笔记
目录前言第1章 写在前面第2章 HTML 语法基础第3章 布局类元素 ,房子的楼板、柱子和大梁第4章 功能类元素,房子的门、窗、水管和电气第5章 CSS基础第6章 选择器,确定样式的作用范围选择器类型选择器的组合使用第7章 权重,样式发送冲…...

【沐风老师】3DMAX几何投影插件Geometry Projection使用详解
【几何投影插件】 描述 3DMAX几何投影插件Geometry Projection,将一个或多个对象或它的顶点选择沿全局或局部 x、y 或 z 轴投影到另一个对象上。 适用版本 3dMax2013或更高版本 安装设置 插件的安装非常简单,解压后把插件脚本 “geometry_projectio…...

面试问题整理
20200422面试题 1、有nginx为什么还要用gateway 2、factorybean和beanfactory有什么区别 https://www.cnblogs.com/leeego-123/p/12159574.html 2、aop原理 3、ioc原理 4、注解requestbody和responsebody区别。pathvireable和requestparam注解区别,feign客户端的注解…...

“区块链60人”2022赋能中国区块链创新人物名单公布
2022年11月5日,“2022第五届全国高校人工智能大数据区块链教育教学创新论坛”在京隆重召开。此次论坛公布了“区块链60人”2022赋能中国区块链创新人物评选活动获评名单。 本次评选活动通过媒体报道、第三方推荐、专家评选等环节,坚持“公开、公平、公正…...

day2324 数组
文章目录相关概念codeArrayTest08 数组拷贝相关概念 day23课堂笔记 1、数组 1.1、数组的优点和缺点,并且要理解为什么。 第一:空间存储上,内存地址是连续的。 第二:每个元素占用的空间大小相同。 第三:知道首元素的内…...

【Python实战】神仙运气—快看看你的彩票:2千多万元大奖无人领,马上就过期了,下一期的中奖者会是你吗?(纯技术交流)
前言 越努力越幸运 哈喽~我是栗子同学! 特别注意:不管是沉迷赌球,还是沉迷购彩,都是不可取的。本文纯是一个技术学习内容。 听说关注我的人会暴富哦!、 所有文章完整的素材源码都在👇👇 粉丝…...

2023年上半年软考高项信息系统项目管理师2月25日开班
信息系统项目管理师是全国计算机技术与软件专业技术资格(水平)考试(简称软考)项目之一,是由国家人力资源和社会保障部、工业和信息化部共同组织的国家级考试,既属于国家职业资格考试,又是职称资…...
数据库(第一天)
文档信息 文档类别正式文档文档编号数据库基础课 1.2-001版本1.2-001文档名称数据库基础课编写负责人/编写时间梁昭东/2023 年 1 月 30 日审核负责人/审核时间年 月 日批准人/批准时间年 月 日 变更记录 日期版本号变更内容修订者2023.01.30v1.2版根据实际情况增删了部分内容…...

一文了解 ArrayList 的扩容机制
了解 ArrayList 在 Java 中常用集合类之间的关系如下图所示: 从图中可以看出 ArrayList 是实现了 List 接口,并是一个可扩容数组(动态数组),它的内部是基于数组实现的。它的源码定义如下: public class A…...

牛态已成选股源码
{牛态已成} {条件选股} {其他类型} N:7; A1:(REF(H,N) HHV(H,((2 * N) 1))); B1:FILTER(A1,N); C1:BACKSET(B1,(N 1)); D1:FILTER(C1,N); A2:(REF(L,N) LLV(L,((2 * N) 1))); B2:FILTER(A2,N); C2:BACKSET(B2,(N 1)); D2:FILTER(C2,N); E1:((REF(LLV(L,(2 * N)),1) REF(…...

Python基础
Python 是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。Python 的设计具有很强的可读性,相比其他语言经常使用英文关键字,其他语言的一些标点符号,它具有比其他语言更有特色语法结构。小编也整理了一套关于学习Python入门…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
