Dijkstra 算法 是什么?
Dijkstra 算法
Dijkstra 算法是一种经典的最短路径算法,用于在图(有向或无向图)中找到从起点到其他所有节点的最短路径。它以广度优先搜索的方式,逐步扩展到目标节点,确保计算出的路径是最短的。
1. Dijkstra 算法的基本概念
特点
- 适用于非负权值的图。
- 能够找到从单一源节点到所有其他节点的最短路径。
输入
- 一个图(节点和边)。
- 起始节点(源节点)。
输出
- 从起始节点到其他所有节点的最短路径长度。
- 如果需要,可以记录路径上的具体节点。
2. 核心思想
Dijkstra 算法的核心思想是:
- 利用贪心策略,每次选择当前未访问的、距离起点最近的节点进行扩展。
- 一旦访问一个节点,其最短路径就不会被更新(路径确定性)。
3. 算法步骤
初始化
- 创建一个距离表(distance table):
- 对每个节点初始化为无穷大(∞),表示当前未知最短路径。
- 起点的距离设为 0:
distance[start] = 0。
- 创建一个访问表(visited set),记录已访问的节点。
- 使用一个优先队列或小顶堆(priority queue)存储待访问节点及其距离。
主循环
- 从优先队列中取出距离起点最近的未访问节点 ( u )。
- 对 ( u ) 的每个邻居节点 ( v ):
- 计算从起点通过 ( u ) 到 ( v ) 的路径距离:
distance[v] = min(distance[v], distance[u] + weight(u, v))。 - 如果路径距离更新了,将 ( v ) 加入优先队列。
- 计算从起点通过 ( u ) 到 ( v ) 的路径距离:
- 将 ( u ) 标记为已访问。
- 重复上述步骤,直到优先队列为空或所有节点的最短路径确定。
路径恢复
如果需要输出路径,可以在更新距离表时记录每个节点的前驱节点,最后从目标节点回溯到起点。
4. 伪代码
Dijkstra(Graph, Start):# 初始化distance = {node: ∞ for node in Graph}distance[Start] = 0visited = set()priority_queue = [(0, Start)] # (distance, node)while priority_queue:# 取出当前距离最小的节点current_distance, current_node = priority_queue.pop()if current_node in visited:continuevisited.add(current_node)# 更新邻居节点的距离for neighbor, weight in Graph[current_node]:new_distance = current_distance + weightif new_distance < distance[neighbor]:distance[neighbor] = new_distancepriority_queue.append((new_distance, neighbor))return distance
5. 示例
图示
假设一个加权图如下:
(A)--1--(B)--4--(D)| |2 2| |(C)--1--(E)
输入
- 起点:
A - 图的权值:
Graph = {A: [(B, 1), (C, 2)], B: [(A, 1), (D, 4), (E, 2)], C: [(A, 2), (E, 1)], ...}
执行步骤
- 初始化:
distance = {A: 0, B: ∞, C: ∞, D: ∞, E: ∞}。 - 选择 ( A ) 开始,更新邻居:
- ( distance[B] = 0 + 1 = 1 )
- ( distance[C] = 0 + 2 = 2 )
- 选择 ( B ):
- ( distance[D] = 1 + 4 = 5 )
- ( distance[E] = 1 + 2 = 3 )
- 选择 ( C ):
- ( distance[E] = min(3, 2 + 1) = 3 )
- 选择 ( E )、( D ),最终得到:
distance = {A: 0, B: 1, C: 2, D: 5, E: 3}。
输出
从 ( A ) 到各节点的最短路径距离:
- ( A \to B: 1 )
- ( A \to C: 2 )
- ( A \to D: 5 )
- ( A \to E: 3 )
6. 优缺点
优点
- 高效:适用于稠密图,时间复杂度为 ( O((V + E) \log V) )(使用堆实现)。
- 稳定:保证找到从起点到各节点的最短路径。
缺点
- 限制:不能处理带负权边的图。
- 局限性:只能从一个起点出发计算最短路径,无法同时处理多源问题。
7. 应用场景
- 导航系统:计算最短路径(如 Google Maps)。
- 网络路由:最优路由规划(如 OSPF 协议)。
- 游戏开发:角色移动规划。
- 交通规划:优化物流路径。
如果需要更详细的代码示例或具体实现,可以进一步探讨!
相关文章:

Dijkstra 算法 是什么?
Dijkstra 算法 Dijkstra 算法是一种经典的最短路径算法,用于在图(有向或无向图)中找到从起点到其他所有节点的最短路径。它以广度优先搜索的方式,逐步扩展到目标节点,确保计算出的路径是最短的。 1. Dijkstra 算法的基…...

英文输入法---华为OD机试2024年E卷
题解: 代码:...

理解 package.json 中版本号符号
今天,聊一聊在前端开发中, package.json 中怎么看版本号符号。 版本号符号的解释 版本号通常由三部分组成:主版本号、次版本号、补丁版本号,格式为 major.minor.patch。常见的符号有: ^:更新时允许自动…...
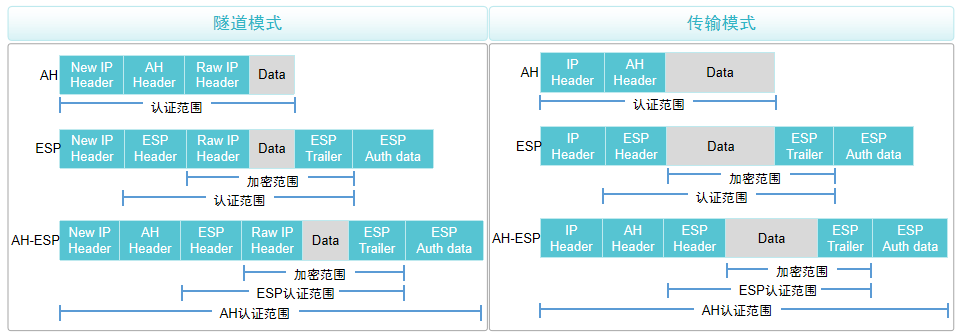
计算机网络-IPSec VPN基本概念
企业分支之间经常有互联的需求,企业互联的方式很多,可以使用专线线路或者Internet线路。部分企业从成本和需求出发会选择使用Internet线路进行互联,但是使用Internet线路存在安全风险,如何保障数据在传输时不会被窃取?…...

VsCode运行Ts文件
1. 生成package.json文件 npm init 2. 生成tsconfig.json文件 tsc --init 3. Vscode运行ts文件 在ts文件点击右键执行Run Code,执行ts文件...

模型 AITDA(吸引、兴趣、信任、渴望、行动)
系列文章 分享 模型,了解更多👉 模型_思维模型目录。吸引、兴趣、信任、渴望、行动 五步曲。 1 模型AITDA的应用 1.1 开源AI智能名片小程序的营销策略 一家企业开发了开源AI智能名片小程序,旨在通过S2B2C模式连接供应商和消费者。该企业采用…...

十、软件设计架构-微服务-服务调用Feign
文章目录 前言一、Feign介绍1. 什么是Feign2. 什么是Http客户端3. Feign 和 OpenFeign 的区别 二、Feign底层原理三、Feign工作原理详解1. 动态代理机制2. 动态代理的创建过程3. 创建详细流程4. FeignClient属性 四、Feign使用1. 常规调用2.日志打印3. 添加Header 前言 服务调…...
电子商务人工智能指南 3/6 - 聊天机器人和客户服务
介绍 81% 的零售业高管表示, AI 至少在其组织中发挥了中等至完全的作用。然而,78% 的受访零售业高管表示,很难跟上不断发展的 AI 格局。 近年来,电子商务团队加快了适应新客户偏好和创造卓越数字购物体验的需求。采用 AI 不再是一…...

【AI模型对比】Kimi与ChatGPT的差距:真实对比它们在六大题型中的全面表现!
文章目录 Moss前沿AI语义理解文学知识数学计算天文学知识物理学知识英语阅读理解详细对比列表总结与建议 Moss前沿AI 【OpenAI】获取OpenAI API Key的多种方式全攻略:从入门到精通,再到详解教程!! 【VScode】VSCode中的智能AI-G…...

spring6:2入门
spring6:2入门 目录 spring6:2入门2.1、环境要求2.2、构建模块2.3、程序开发2.3.1、引入依赖2.3.2、创建java类2.3.3、创建配置文件2.3.4、创建测试类测试2.3.5、运行测试程序 2.4、程序分析2.5、启用Log4j2日志框架2.5.1、Log4j2日志概述2.5.2、引入Log…...

Netty - NIO基础学习
一 简介 1 三大模型是什么? IO三大模型之一,BIO,AIO,还有我们的主角NIO(non-blocking-io),也就是同步非阻塞式IO。这三种模型到底是干什么的?其实这三种模型都是对于JAVA的一种I/O框架,用来进行…...

ArrayList的自动扩容机制源码
Java的ArrayList的自动扩容机制 ArrayList是 Java 中极为常用的动态数组实现类,它依托数组存储数据,能依据实际需求灵活变动容量,高效管理元素集合。在深挖底层源码细节前,先来了解创建ArrayList集合并添加元素时的运作流程&#…...
)
【llm_inference】react框架(最小code实现)
ReAct:结合推理和行动的大语言模型推理架构 GitHub Code: 人人都能看懂的最小实现 引言 在人工智能领域,大语言模型(LLM)的应用日益广泛,但如何让模型能够像人类一样,在思考的基础上采取行动,…...

PT8M2103 触控 I/O 型 8-Bit MCU
1 产品概述 ● PT8M2103 是一款可多次编程(MTP)I/O 型8位 MCU,其包括 2K*16bit MTP ROM、256*8bit SRAM、PWM、Touch 等功能,具有高性能精简指令集、低工作电压、低功耗特性且完全集成触控按键功能。为各种触控按键的应用,提供了一种简单而又…...

英语时态学习+名词副词形容词变形方式
开发出头不容易 不如跨界卷英语 英语中的16种时态是由四种时间(现在、过去、将来、过去将来)和四种体(一般、进行、完成、完成进行)组合而成的。以下是每种时态的详细说明和例句: 一般现在时 (Simple Present) 用法…...

浏览器解析页面流程
从输入一个url到页面解析完成的流程 1. 网络进程 1. 获取url 浏览器首先判断输入的url是否有http缓存,如果有则直接从http缓存中读取数据并显示。如果没有,则进行下一步。进行DNS解析,获取域名对应的IP地址。 2.下载html文件 浏览器根据I…...

图的遍历之DFS邻接矩阵法
本题要求实现一个函数,对给定的用邻接矩阵存储的无向无权图,以及一个顶点的编号v,打印以v为起点的一个深度优先搜索序列。 当搜索路径不唯一时,总是选取编号较小的邻接点。 本题保证输入的数据(顶点数量、起点的编号等…...

Java --- JVM编译运行过程
目录 一.Java编译与执行流程: 二.编译过程: 1.编译器(javac): 2.字节码文件(.class): 三.执行过程: 1.启动JVM(Java虚拟机): 2…...

HTML5 拖拽 API 深度解析
一、HTML5 拖拽 API 深度解析 1.1 背景与发展 HTML5 的拖拽 API 是为了解决传统拖拽操作复杂而设计的。传统方法依赖鼠标事件和复杂的逻辑计算,而 HTML5 提供了标准化的拖拽事件和数据传递机制,使得开发者能够快速实现从一个元素拖拽到另一个元素的交互…...
GO--基于令牌桶和漏桶的限流策略
至于为什么要限流,字面意思已经很清楚了,就是为了减轻服务器的压力 下面我们将介绍两个限流策略----漏桶和令牌桶。 漏桶 原理介绍 漏桶,顾名思义就是一个漏斗,漏斗嘴的大小是固定的,所以不管漏斗现容量多大&#…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
