教学案例：k相同的一次函数的图像关系

【题目】

请在同一个平面直角坐标系中画出一次函数y=2x, y=2x+4的图象，并观察图象，你发现这两个图形有什么位置关系？为什么？

【答案】

图象是相互平行的两条直线

【解析】

一、教学活动形式

这里设计的教学活动形式是“画图 → 观察→ 猜想 → 验证 → 证明”。

1．画图

通过描点连线，画出两个一次函数的图像。

2．观察

你俩关系太明显，一眼就能看出。

3．猜想

这俩函数有啥共同之处，对了，一次项的系数相同。那么是不是K相同的一次函数都平行呢？让孩子们的思维飞一会儿，大家伙儿一起研究研究，讨论讨论。

4．验证

再画一个试试，来个y=2x-4看看。不行就再画两个，看看是不是都有这个规律？

5．证明

之前都只是“看着”平行，你还要用演绎推理的方式证明这两个函数平行。

注意验证和证明的区别：验证是通过举例子、做实验的方法来检验结论；证明则是运用已知定理、公理，通过逻辑推理的方式，从已知条件出发推导出结论。

(1)个例证明

如图所示，函数y=2x+4与坐标轴交于A、B两点，故A点纵坐标为0、B点横坐标为0，代入函数可求得A、B的坐标分别是A(-2,0), B(0,4)。在直线y=2x上取纵坐标为4的点C，由点C向x轴画垂线，垂足为D。纵坐标为4（CD=4），代入函数，可求得横坐标为2（0D=2）。则△AOB≌△OD C(SAS)得∠BAO=∠COD，从而有AB∥CD。

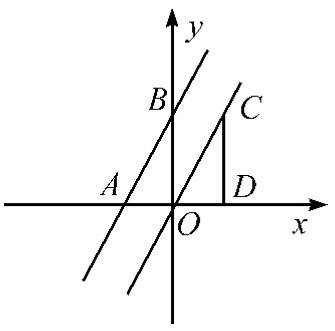
然而，这只是证明了y=2x, y=2x+4这两个函数平行，并不能由此得出结论“一次项系数k相同的一次函数相互平行”。

(2)命题证明

要再进一步引导学生证明上述命题成立，即一般形式的y=kx,y=kx+b具有平行关系。

其实证明思路和前面完全一样，只需用字母代替前面的数即可（代数法）。

同样可以求出函数y=kx+b与坐标轴交点的坐标为(-b/k, 0)，(0, b)，在函数y=kx上取纵坐标为b的点，该点的坐标为(b/k, b)。于是，我们同样能通过证明两个三角形相等的形式证明两直线平行。

二、总结反思

这道题的证明首先要画辅助线构造三角形，再通过证明三角形全等得出同位角相等，进而证明两直线平行。

问题来了，我们是怎么想到解题思路的呢？

一切都要从问题出发。

要证明两直线平行，只有通过角的关系证明。只有三种渠道：同位角相等、内错角相等、同旁内角互补。

你要明白，这三种方法其实只是一种。因为后两种都是由第一种推导出来的。

第一种是最直接、最直观的证明方法，应该是我们首选的证明方法。

第二种次之，第三种因为不能通过角相等证明，因此很少用。

无论哪种证明方法，都需要有“截线”（与两条平行线都相交的线，即截断两条线的线）。

画面上正有两条天然截线：X轴、Y轴。

要证明角相等，那全等三角形是不二之选。

你一眼看过去，画面上已有一个三角形，就是y=kx+b与坐标轴构成的那个三角形。

所以自然会想到以y=kx为一条边，再构造一个三角形，与这个三角形相等，于是你想到要画辅助线。

怎么画辅助线呢？看看画面上已有的那个三角形，两条直角边，一条斜边。斜边有了，所以你肯定是要画直角边了。

前面给出的证明方法是画平行于Y轴的辅助线构造三角形，能不能用平行于X轴的辅助线构造全等三角形呢？当然可以！

能不能通过内错角相等证明呢，当然也可以，无非要构造的三角形不同，要画的辅助线不同而已。

最后，总结下证明思路：证明平行←同位角相等←全等三角形←画辅助线构造三角形。