day35—蓝桥杯2024年第16届校赛模拟第二期-T4(最小花费)
【问题描述】
小蓝有一个整数,初始值为 1 ,他可以花费一些代价对这个整数进行变换。
小蓝可以花费 1 的代价将整数增加 1 。
小蓝可以花费 3 的代价将整数增加一个值,这个值是整数的数位中最大的那个(1 到 9)。
小蓝可以花费 10 的代价将整数变为原来的 2 倍。
例如,如果整数为 16,花费 3 将整数变为 22 。
又如,如果整数为 22,花费 1 将整数变为 23 。
又如,如果整数为 23,花费 10 将整数变为 46 。
请问,如果要将整数从初始值 1 变为 2024,请问最少需要多少代价?【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
#include <iostream> #include <algorithm> #include <cstring>using namespace std;int max_digit(int n) {int res=0;while(n){res=max(res,n%10);n/=10;}return res; }//分离数位,返回最大值 int dp[5000]; int main() {//dp[n]:花费// n:变化的值memset(dp,0x3f,sizeof dp);dp[1]=0;//初始条件:dp=maxfor(int i=1;i<=2050;i++){//反复遍历更新,取各自最小值即为最小花费//逻辑命题dp[i+1]=min(dp[i+1],dp[i]+1);// dp:0 1 2 3 ... // n:1 2 3 4 ...//花费 1:累加即可//确定为:dp[2]=1dp[i+max_digit(i)]=min(dp[i+max_digit(i)],dp[i]+3);// dp:0 3/1 6/3 ... // n:1 2 4 ...//确定为:dp[2]=1(更新)dp[2*i]=min(dp[2*i],dp[i]+10);//花费 10://0 10/1/3 ...//1 2 4 8 16//确定为:dp[2]=1(更新)}for(int i=0;i<2025;i++) cout<<dp[i]<<" ";//调试打印代码cout<<endl<<dp[2024]<<endl;return 0; }
相关文章:
)
day35—蓝桥杯2024年第16届校赛模拟第二期-T4(最小花费)
【问题描述】 小蓝有一个整数,初始值为 1 ,他可以花费一些代价对这个整数进行变换。 小蓝可以花费 1 的代价将整数增加 1 。 小蓝可以花费 3 的代价将整数增加一个值,这个值是整数的数位中最大的那个(1 到 9)。 小蓝可…...

【CSS in Depth 2 精译_068】11.2 颜色的定义(下):CSS 中的各种颜色表示法简介
当前内容所在位置(可进入专栏查看其他译好的章节内容) 第四部分 视觉增强技术 ✔️【第 11 章 颜色与对比】 ✔️ 11.1 通过对比进行交流 11.1.1 模式的建立11.1.2 还原设计稿 11.2 颜色的定义 11.2.1 色域与色彩空间11.2.2 CSS 颜色表示法 ✔️ 11.2.2.…...

游戏引擎学习第38天
仓库: https://gitee.com/mrxiao_com/2d_game 回顾上次的内容。 我们之前讨论了将精灵放在屏幕上,但颜色错误的问题。问题最终查明是因为使用了一个调整工具,导致文件的字节顺序发生了变化。重新运行“image magic”工具对一些大图像进行重新处理后&am…...
)
P1223 排队接水(贪心)
题目描述 有 𝑛个人在一个水龙头前排队接水,假如每个人接水的时间为 𝑇𝑖,请编程找出这 𝑛 个人排队的一种顺序,使得 𝑛个人的平均等待时间最小。 输入格式 第一行为一个整数 &am…...

关于springBoot+vue项目中配置SSL证书问题
前端可以通过https进行访问 1.前端在访问后端接口时,使用https进行访问,在request.js配置文件中,这个文件是配置axios的基本请求的,在基础请求地址中改为https方式 2.需要在Linux中的nginx中配置ssl证书,具体请参考&…...

GUI的最终选择:Tkinter
Tkinter是Python默认的GUI库,因此使用时直接导入即可:import tkinter 17.1 Tkinter之初体验 代码分析: tkinter.mainloop()通常是程序的最后一行代码,执行后程序进入主事件循环。 17.2 进阶版本 将代码封装成类: 运…...

Photohop关于数位板没有压力感,PS画笔的钢笔压力总是显示感叹号的问题解放方法
(实际我只用到红色字2步解决了问题,但为了兼顾更多朋友,还是把其他步骤详细完善) 一,先确定数位板正常链接电脑,并安装好驱动,并在驱动测试到压力 二,解决PS前感叹号问题 …...

rust websocket Echo server高性能服务器开发
最近在学习websocket时,一直没有发现好的websocket server工具来调试,于是就自己做了一个websocket server用来学习和调试。因为rust性能遥遥领先,所以就采用了rust来搭建服务器。废话不多说直接上代码main.rs: use tokio::net::TcpListener; use tokio_tungstenite::tung…...

19、网络编程:
19、网络编程: 网络的相关概念: 网络通讯: 概念:两台设备之间通过网络实现数据传输;网络通讯:将数据通过网络从一台设备传输到另一台设备;java.net包下提供了一系列的类或接口,供…...

[代码随想录11]栈和队列的应用,逆波兰表达式求值 、滑动窗口最大值、前 K 个高频元素
前言 这几个题目都是栈和队列的高频面试题目,主要是考察思路和coding能力,在前面几道题目的基础上进行延伸的。同时还有优先级队列和双端队列的用法 题目链接 150. 逆波兰表达式求值 - 力扣(LeetCode) 239. 滑动窗口最大值 - 力…...

认证插件介绍
本文档是针对 UOS 登录器插件给出开发指南,目的是为了让开发人员了解如何在 UOS 登录器上增加一种自定义认证方式,对插件接口做了详细说明以及实战练习。 文章目录 一、认证插件可以做什么?二、认证流程三、术语说明四、安全性五、可靠性六、…...

ASP.NET Core8.0学习笔记(二十四)——EF Core级联插入与删除
一、EF Core导航关系操作——级联插入 1.级联插入:在含有导航属性的实体(主体实体)中可以对实体进行级联插入。即在创建主体实体时直接把依赖实体进行赋值,此时只需要执行一次插入操作即可将主体实体与依赖实体同时入库。同时&am…...

Docker打包SpringBoot项目
一、项目打成jar包 在进行docker打包之前,先确定一下,项目能够正常的打成JAR包,并且启动之后能够正常的访问。这一步看似是可有可无,但是能避免后期的一些无厘头问题。 二、Dockerfile 项目打包成功之后,需要编写Doc…...

【Linux】WSL:Win运行Linux
WSL2(Windows Subsystem for Linux 2) 是 Microsoft 开发的技术,可在 Windows 系统上运行完整的 Linux 发行版环境。以下是详细的配置教程。 安装与配置 启用 WSL 功能 打开“开始”菜单,搜索 PowerShell,以 管理员身…...
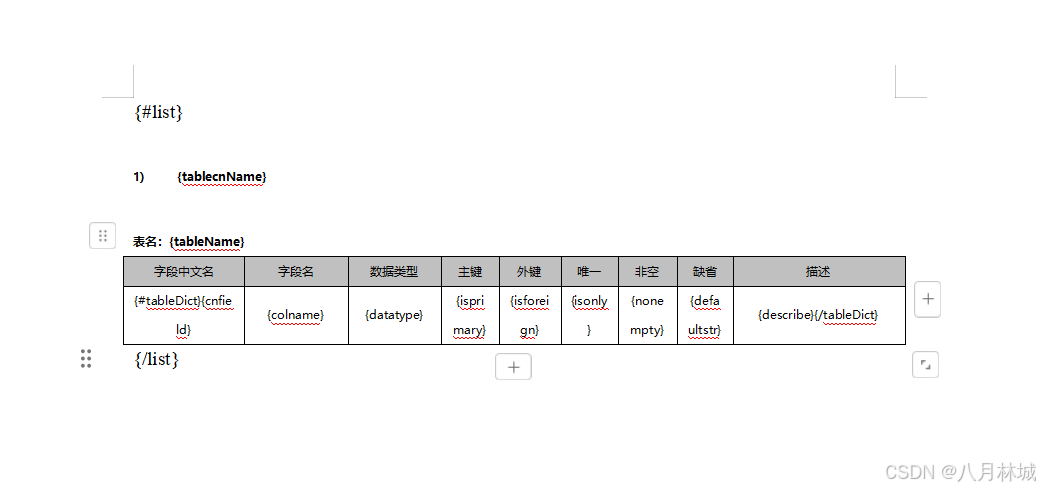
js循环导出多个word表格文档
文章目录 js循环导出多个word表格文档一、文档模板编辑二、安装依赖三、创建导出工具类exportWord.js四、调用五、效果图js循环导出多个word表格文档 结果案例: 一、文档模板编辑 二、安装依赖 // 实现word下载的主要依赖 npm install docxtemplater pizzip --save// 文件操…...

Spring Boot 日志 配置 SLF4J 和 Logback
前言 在开发 Java 应用时,日志记录是不可或缺的一部分。日志可以记录应用的运行状态、错误信息和调试信息,帮助开发者快速定位和解决问题。Spring Boot 项目默认集成了 SLF4J 和 Logback,使得日志配置变得简单而灵活。本文将详细介绍如何在 …...
)
企业级包管理器:专栏概述 (1)
在当今的前端开发领域,包管理器已经成为了每一位开发者不可或缺的工具。它们就像一个个神奇的工具箱,里面装满了各种各样的工具(即软件包),帮助我们快速搭建项目、实现功能,极大地提高了开发效率。接下来&a…...

【动手学电机驱动】STM32-MBD(1)安装 STM32 硬件支持包
STM32-MBD(1)安装 STM32 硬件支持包 【动手学电机驱动】STM32-MBD(1)安装 STM32 硬件支持包 1. 必须的软硬件条件2. 嵌入式硬件支持包2.1 Embedded Coder2.2 嵌入式硬件支持包2.3 Embedded Coder Support Package for STMicroelec…...
》,电子工业出版社,2020.01)
书后习题答案:《Python程序设计基础(第2版)》,电子工业出版社,2020.01
【持续更新】 第3章 from math import *x1 float(input("请输入x1: ")) # print(x1) x2 float(input("请输入x2: ")) y1 float(input("请输入y1: ")) y2 float(input("请输入y2: "))dis sqrt(pow(x1 - x2, 2) pow(y1 - y2, 2))…...

Qt之第三方库QXlsx使用(三)
Qt开发 系列文章 - QXlsx(三) 目录 前言 一、Qt开源库 二、QXlsx 1.QXlsx介绍 2.QXlsx下载 3.QXlsx移植 4.修改项目文件.pro 三、使用技巧 1.添加头文件 2.写入数据 3.读出数据 总结 前言 Qt第三方控件库是指非Qt官方提供的、用于扩展Qt应用…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...
