【uniapp】swiper切换时,v-for重新渲染页面导致文字在视觉上的拉扯问题
问题描述
先用v-for渲染了几个列表,但这几个列表是占同一个位置的,只是通过切换swiper来显示哪个列表显示,也就是为了优化页面切换时候,没有根据swiper的current再更新v-for的数据,但现在就有个问题,怎么隐藏这些列表,并且不占dom。v-if控制的时候,会出现非常明显的重新渲染的闪屏现象。
解决方法
使用position: absolute和clip属性
绝对定位与裁剪:
将元素设置为position: absolute,它就脱离了文档流,不再影响页面布局。然后通过clip属性来裁剪元素,当裁剪区域设置为0时,元素在视觉上就被隐藏了。这种方式下元素仍然在DOM中,但不占据布局空间,并且避免了v - if的重新渲染闪屏问题。
<template><div><swiper :options="swiperOptions"><swiper-item v-for="(list, index) in lists" :key="index"><div :class="{ 'hidden-class': shouldHide(index) }"><!-- 这里渲染列表内容 --><ul><li v-for="item in list" :key="item.id">{{item.name}}</li></ul></div></swiper-item ></swiper></div>
</template><script>
export default {data() {return {currentIndex: 0,lists: [[{id: 1, name: 'List 1-Item 1'},{id: 2, name: 'List 1-Item 2'}],[{id: 3, name: 'List 2-Item 1'},{id: 4, name: 'List 2-Item 2'}]],swiperOptions: {// Swiper的配置选项}};},methods: {shouldHide(index) {return this.currentIndex!== index;}},
};
</script><style> .hidden-class{position: absolute; clip: rect(0, 0, 0, 0);}
</style>相关文章:

【uniapp】swiper切换时,v-for重新渲染页面导致文字在视觉上的拉扯问题
问题描述 先用v-for渲染了几个列表,但这几个列表是占同一个位置的,只是通过切换swiper来显示哪个列表显示,也就是为了优化页面切换时候,没有根据swiper的current再更新v-for的数据,但现在就有个问题,怎么隐…...

【Android】Compose初识
文章目录 1.Compose是什么2.Compose优势3.可组合函数4.布局5.配置布局6.Material Design7.列表与动画8.声明式UI9.组合10.重组 1.Compose是什么 Jetpack Compose是谷歌开发的一个现代的、声明式的UI工具包,用于构建原生的Android应用程序界面。它简化了创建复杂用户…...
)
前端工程化面试题(二)
前端模块化标准 CJS、ESM 和 UMD 的区别 CJS(CommonJS)、ESM(ESModule)和UMD(Universal Module Definition)是前端模块化标准的三种主要形式,它们各自有不同的特点和使用场景: CJS&…...

以攻击者的视角进行软件安全防护
1. 前言 孙子曰:知彼知己者,百战不殆;不知彼而知己,一胜一负,不知彼,不知己,每战必殆。 摘自《 孙子兵法谋攻篇 》在2500 年前的那个波澜壮阔的春秋战国时代,孙子兵法的这段话&…...

008.精读《Apache Paimon Docs - Table w/o PK》
文章目录 1. 引言2. 基本概念2.1 定义2.2 使用场景 3. 流式处理3.1 自动小文件合并3.2 流式查询 4. 数据更新4.1 查询4.2 更新4.3 分桶附加表 5 总结 1. 引言 通过本文,上篇我们了解了Apache Paimon 主键表,本期我们将继续学习附加表(Append…...
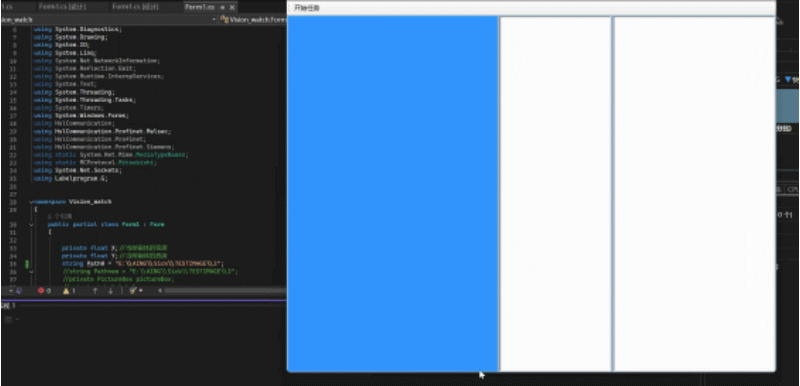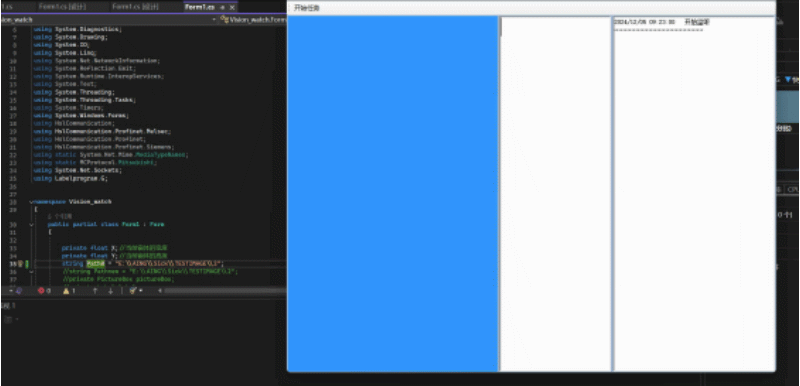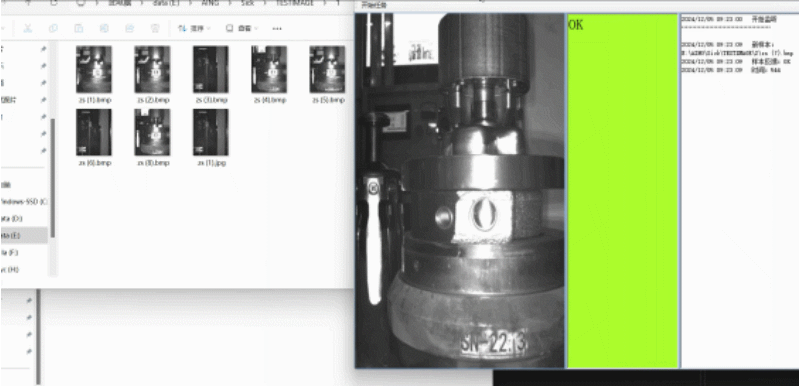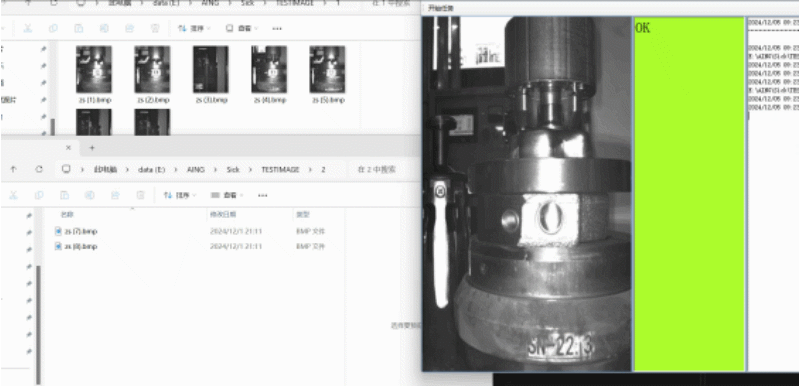
C#实时监控指定文件夹中的动态,并将文件夹中生成的新图片显示在界面上(相机采图,并且从本地拿图)
结果展示 此类原理适用于文件夹中自动生成图片,并提取最新生成的图片将其显示, 如果你是相机采图将其保存到本地,可以用这中方法可视化,并将检测的结果和图片匹配 理论上任何文件都是可以监视并显示的,我这里只是做了…...

使用SQLark分析达梦慢SQL执行计划的一次实践
最近刚参加完达梦的 DCP 培训与考试,正好业务系统有个 sql 查询较慢,就想着练练手。 在深入了解达梦的过程中,发现达梦新出了一款叫 SQLark 百灵连接的工具。 我首先去官网大致浏览了下。虽然 SQLark 在功能深度上不如 DM Manager 和 PL/SQ…...

【人工智能】用Python构建高效的自动化数据标注工具:从理论到实现
《Python OpenCV从菜鸟到高手》带你进入图像处理与计算机视觉的大门! 数据标注是构建高质量机器学习模型的关键环节,但其耗时耗力常成为制约因素。本篇文章将介绍如何用Python构建一个自动化数据标注工具,结合机器学习和NLP技术,帮助加速数据标注过程。我们将从需求分析入…...
)
Java --- 注解(Annotation)
一.什么是注解? 在Java中,注解(Annotation)是一种元数据(metadata),它为程序中的类、方法、字段等提供额外的描述信息。注解本身不直接改变程序的行为,但可以被编译器、开发工具、框…...

nodejs作为provider接入nacos
需求:公司产品一直是nodejs的后台,采用的eggjs框架,也不是最新版本,现有有需求需求将这些应用集成到微服务的注册中心,领导要求用java。 思路:用spring cloud gateway将需要暴露的接口url转发,…...

SpringBoot3+Micormeter监控应用指标
监控内容简介 SpringBoot3项目监控服务 ,可以使用Micormeter度量指标库,帮助我们监控应用程序的度量指标,并将其发送到Prometheus中并用Grafana展示。监控指标有系统负载、内存使用情况、应用程序的响应时间、吞吐量、错误率等。 micromete…...

Mybatis-plus 简单使用,mybatis-plus 分页模糊查询报500 的错
一、mybtis-plus配置下载 MyBatis-Plus 是一个 Mybatis 增强版工具,在 MyBatis 上扩充了其他功能没有改变其基本功能,为了简化开发提交效率而存在。 具体的介绍请参见官方文档。 官网文档地址:mybatis-plus 添加mybatis-plus依赖 <depe…...

2022 年 12 月青少年软编等考 C 语言三级真题解析
目录 T1. 鸡兔同笼思路分析T2. 猴子吃桃思路分析T3. 括号匹配问题T4. 上台阶思路分析T5. 田忌赛马T1. 鸡兔同笼 一个笼子里面关了鸡和兔子(鸡有 2 2 2 只脚,兔子有 4 4 4 只脚,没有例外)。已经知道了笼子里面脚的总数 a a a,问笼子里面至少有多少只动物,至多有多少只…...

webpack 题目
文章目录 webpack 中 chunkHash 和 contentHash 的区别loader和plugin的区别?webpack 处理 image 是用哪个 loader,限制 image 大小的是...;webpack 如何优化打包速度 webpack 中 chunkHash 和 contentHash 的区别 主要从四方面来讲一下区别&…...

【MySQL】视图详解
视图详解 一、视图的概念二、视图的常用操作2.1创建视图2.2查询视图2.3修改视图2.4 删除视图2.5向视图中插入数据 三、视图的检查选项3.1 cascaded(级联 )3.2 local(本地) 四、视图的作用 一、视图的概念 视图(View)是一种虚拟存…...

第一节:ORIN NX介绍与基于sdkmanager的镜像烧录(包含ubuntu文件系统/CUDA/OpenCV/cudnn/TensorRT)
ORIN NX技术参数 Orin NX版本对比 如上图所示,ORIN NX官方发布的版本有两个版本一个版本是70TOPS算力,DDR为8GB的版本低配版本,一个是100TOPS算法,DDR为16GB的高配版本。 Orin NX的外设框图 两个版本除了GPU和DDR的差距外,外设基本上没有区别,丰富的外设接口,后续开发…...

2024-12-04OpenCV视频处理基础
OpenCV视频处理基础 OpenCV的视频教学:https://www.bilibili.com/video/BV14P411D7MH 1-OpenCV视频捕获 在 OpenCV 中,cv2.VideoCapture() 是一个用于捕获视频流的类。它可以用来从摄像头捕获实时视频,或者从视频文件中读取帧。以下是如何使用…...

D89【python 接口自动化学习】- pytest基础用法
day89 pytest的setup,setdown详解 学习日期:20241205 学习目标:pytest基础用法 -- pytest的setup,setdown详解 学习笔记: setup、teardown详解 模块级 setup_module/teardown_module 开始于模块始末,生…...

七、docker registry
七、docker registry 7.1 了解Docker Registry 7.1.1 介绍 registry 用于保存docker 镜像,包括镜像的层次结构和元数据。启动容器时,docker daemon会试图从本地获取相关的镜像;本地镜像不存在时,其将从registry中下载该镜像并保…...

FlightGear+MATLAB+飞行手柄实现实时飞控视景系统
文章目录 一、软件配置二、FlightGearMATLAB联合仿真第一步 复制文件第二步 新建文件夹第三步 打开demo第四步 demo说明第五步 打开Simulink第六步 连接FlightGear第七步 设置FlightGear第八步 生成FlightGear连接文件FlightGear的设置Network的设置File的设置生成.bat文件 第九…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
