C++算法练习day70——53.最大子序和
题目来源:. - 力扣(LeetCode)
题目思路分析
题目:寻找最大子数组和(也称为最大子序和)。
给定一个整数数组 nums,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
思路:
-
暴力解法:最直接的方法是遍历所有可能的子数组,并计算它们的和,然后找出其中的最大值。然而,这种方法的时间复杂度是 O(n^3),对于大型数组来说效率太低。
-
动态规划:我们可以使用动态规划来优化这个问题。定义一个变量
maxnums来记录当前找到的最大子数组和,另一个变量pos来记录当前子数组的和(以当前元素为结尾)。遍历数组时,对于每个元素,我们有两种选择:要么将其加入当前的子数组(即pos + nums[i]),要么开始一个新的子数组(即nums[i])。然后,更新maxnums为maxnums和pos中的较大值。 -
Kadane's Algorithm:上述动态规划方法实际上就是著名的 Kadane's Algorithm。它的核心思想是,在遍历数组时,不断更新以当前元素为结尾的最大子数组和,同时记录全局的最大子数组和。
代码:
#include <vector>
#include <algorithm> // 为了使用 max 函数 class Solution {
public: int maxSubArray(vector<int>& nums) { // 初始化最大子数组和为数组的第一个元素 int maxnums = nums[0]; // 初始化当前子数组和为数组的第一个元素 int pos = nums[0]; // 遍历数组(从第二个元素开始) for (int i = 1; i < nums.size(); i++) { // 更新当前子数组和:要么继续当前子数组,要么开始新的子数组 pos = max(pos + nums[i], nums[i]); // 更新全局最大子数组和 maxnums = max(maxnums, pos); } // 返回全局最大子数组和 return maxnums; }
};知识点摘要
- Kadane's Algorithm:一种用于解决最大子数组和问题的线性时间复杂度算法。
- 动态规划:一种通过将问题分解为更小的子问题来解决问题的方法,通常用于优化问题。
- max 函数:用于比较两个值并返回其中的较大值。
本文介绍了如何使用 Kadane's Algorithm 来解决最大子数组和问题。通过维护两个变量(全局最大子数组和和当前子数组和),我们可以在遍历数组时不断更新它们,并最终得到全局最大子数组和。这种方法的时间复杂度是 O(n),非常高效。希望本文能帮助大家更好地理解最大子数组和问题和 Kadane's Algorithm。
相关文章:

C++算法练习day70——53.最大子序和
题目来源:. - 力扣(LeetCode) 题目思路分析 题目:寻找最大子数组和(也称为最大子序和)。 给定一个整数数组 nums,找到一个具有最大和的连续子数组(子数组最少包含一个元素&#x…...

import是如何“占领满屏“
import是如何“占领满屏“的? 《拒绝使用模块重导(Re-export)》 模块重导是一种通用的技术。在腾讯、字节、阿里等各大厂的组件库中都有大量使用。 如:字节的arco-design组件库中的组件:github.com/arco-design… …...

ceph /etc/ceph-csi-config/config.json: no such file or directory
环境 rook-ceph 部署的 ceph。 问题 kubectl describe pod dragonfly-redis-master-0Warning FailedMount 7m59s (x20 over 46m) kubelet MountVolume.MountDevice failed for volume "pvc-c63e159a-c940-4001-bf0d-e6141634cc55" : rpc error: cod…...

C语言——验证“哥德巴赫猜想”
问题描述: 验证"哥德巴赫猜想" 任何一个大于2的偶数都可以表示为两个质数之和。例如,4可以表示为22,6可以表示为33,8可以表示为35等 //验证"哥德巴赫猜想" //任何一个大于2的偶数都可以表示为两个质数之和…...

Flourish笔记:柱状图(Column chart (grouped))
文章目录 样式设定Chart Type:图表类型Controls & Filters:展示方式Colors:颜色bars:柱子的调整labels:柱子数字标注X axis:横坐标标签Y axis:纵坐标标签Plot BackgroundNumber FormatingLe…...

深度学习案例:DenseNet + SE-Net
本文为为🔗365天深度学习训练营内部文章 原作者:K同学啊 一 回顾DenseNet算法 DenseNet(Densely Connected Convolutional Networks)是一种深度卷积神经网络架构,提出的核心思想是通过在每一层与前面所有层进行直接连接…...

excel文件合并,每个excel名称插入excel列
import pandas as pd import os # 设置文件夹路径 folder_path rC:\test # 替换为您的下载文件夹路径 output_file os.path.join(folder_path, BOM材料.xlsx) # 创建一个空的 DataFrame 用于存储合并的数据 combined_data pd.DataFrame() # 遍历文件夹中的所有文件 for …...

Linux 如何设置特殊权限?
简介 通过使用 setuid、setgid 、sticky,它们是 Linux 中的特殊权限,可以对文件和目录的访问和执行方式提供额外的控制。 命令八进制数字功能setuid4当执行文件时,它以文件所有者的权限运行,而不是执行它的用户的权限运行。setg…...

零基础如何使用ChatGPT快速学习Python
引言 AI编程时代来临,没有编程基础可以快速上车享受时代的红利吗?答案是肯定的。本文旨在介绍零基础如何利用ChatGPT快速学习Python编程语言,开启AI编程之路。解决的问题包括:传统学习方式效率低、缺乏互动性以及学习资源质量参差…...

【开源】一款基于SpringBoot 的全开源充电桩平台
一、下载项目文件 下载源码项目文件口令:动作璆璜量子屏多好/~d1b8356ox2~:/复制口令后,进入夸克网盘app即可保存(如果复制到夸克app没有跳转资源,可以复制粘贴口令到夸克app的搜索框也可以打开(不用点搜索按钮&#…...

AI - RAG中的状态化管理聊天记录
AI - RAG中的状态化管理聊天记录 大家好,今天我们来聊聊LangChain和LLM中一个重要的话题——状态化管理聊天记录。在使用大语言模型(LLM)的时候,聊天记录(History)和状态(State)管理是非常关键的。那我们先…...
JAVA安全—SpringBoot框架MyBatis注入Thymeleaf模板注入
前言 之前我们讲了JAVA的一些组件安全,比如Log4j,fastjson。今天讲一下框架安全,就是这个也是比较常见的SpringBoot框架。 SpringBoot框架 Spring Boot是由Pivotal团队提供的一套开源框架,可以简化spring应用的创建及部署。它提…...

【STM32系列】提升ADC采样精度的方法
资料地址 兆易创新GigaDevice-资料下载兆易创新GD32 MCU ADC简介 ADC转换包括采样、保持、量化、编码四个步骤。的采样电容上,即在采样开关 SW 关闭的过程中,外部输入信号通过外部的输入电阻 RAIN 和以及 ADC 采样电阻 RADC 对采样电容 CADC 充电。采样…...

前端面试如何出彩
1、原型链和作用域链说不太清,主要表现在寄生组合继承和extends继承的区别和new做了什么。2、推荐我的两篇文章:若川:面试官问:能否模拟实现JS的new操作符、若川:面试官问:JS的继承 3、数组构造函数上有哪些…...

Linux 切换用户的两种方法
sudo -su user1 与 su - user1 都可以让当前用户切换到 user1 的身份执行命令或进入该用户的交互式 Shell。但它们在权限认证方式、环境变量继承和 Shell 初始化过程等方面存在一些差异。 权限认证方式 su - user1 su 是 “switch user” 的缩写,默认情况下需要你输…...
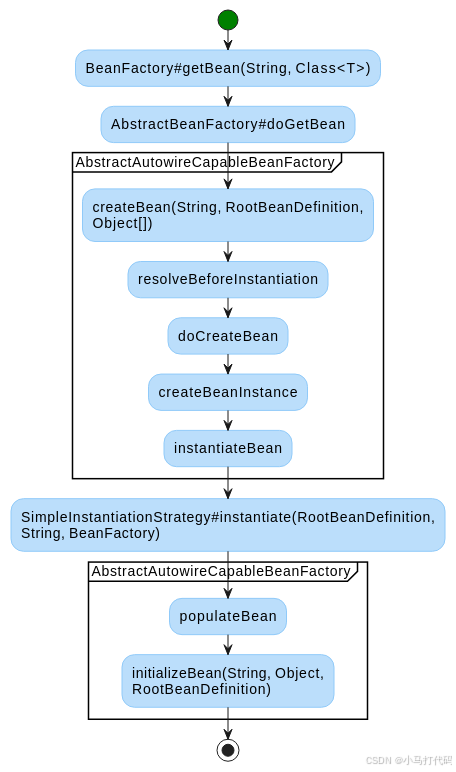
Spring Boot 3 中Bean的配置和实例化详解
一、引言 在Java企业级开发领域,Spring Boot凭借其简洁、快速、高效的特点,迅速成为了众多开发者的首选框架。Spring Boot通过自动配置、起步依赖等特性,极大地简化了Spring应用的搭建和开发过程。而在Spring Boot的众多核心特性中ÿ…...
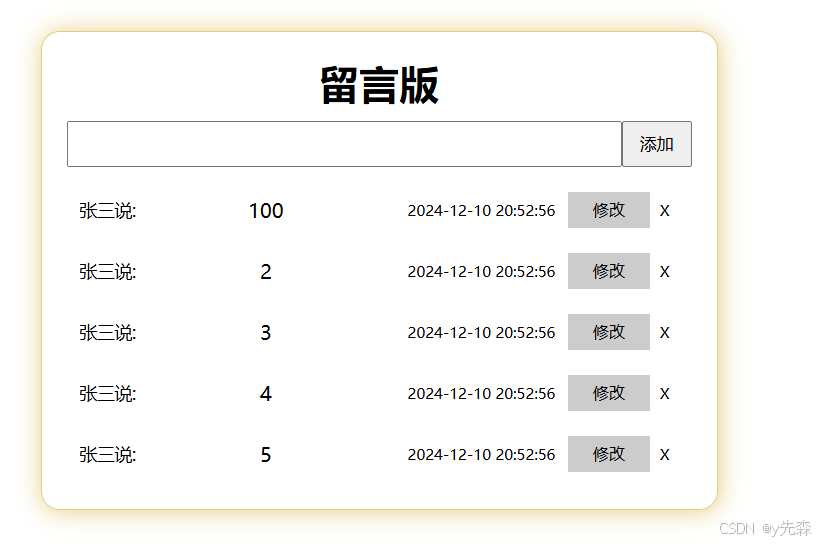
Vue实现留言板(实现增删改查)注意:自己引入Vue.js哦
代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><scri…...
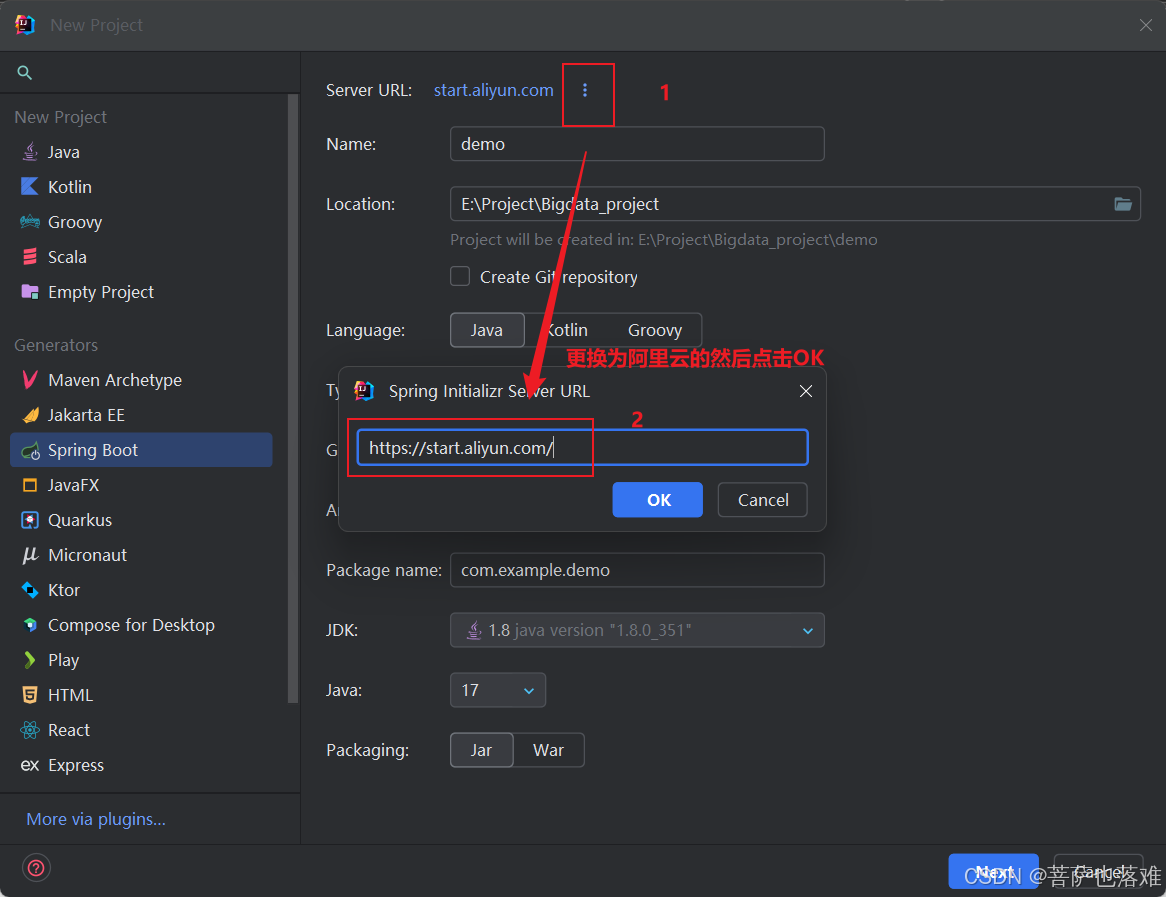
IDEA创建Spring Boot项目配置阿里云Spring Initializr Server URL【详细教程-轻松学会】
1.首先打开idea选择新建项目 2.选择Spring Boot框架(就是选择Spring Initializr这个) 3.点击中间界面Server URL后面的三个点更换为阿里云的Server URL Idea中默认的Server URL地址:https://start.spring.io/ 修改为阿里云Server URL地址:https://star…...
读取电视剧MP4视频的每一帧,检测出现的每一个人脸并保存
检测效果还不错,就是追踪有点难做 import cv2 import mediapipe as mp import os from collections import defaultdict# pip install msvc-runtime# 初始化OpenCV的MultiTracker # multi_tracker = cv2.MultiTracker_create() # multi_tracker = cv2.legacy.MultiTracker_cre…...

HTML前端开发-- Iconfont 矢量图库使用简介
一、SVG 简介及基础语法 1. SVG 简介 SVG(Scalable Vector Graphics)是一种基于 XML 的矢量图形格式,用于在网页上显示二维图形。SVG 图形可以无限缩放而不会失真,非常适合用于图标、图表和复杂图形。SVG 文件是文本文件&#x…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
