AtCoder Beginner Contest 383
C - Humidifier 3
Description
一个 h × w h \times w h×w 的网格,每个格子可能是墙、空地或者城堡。
一个格子是好的,当且仅当从至少一个城堡出发,走不超过 d d d 步能到达。(只能上下左右走,不能穿墙),求好格子的数量。
Solution
从每一个城堡出发进行 bfs,对所有 d 步内能走到的点进行标记。
为了效率,可以把所有城堡丢入队列中,一次搜完。
Code
// Problem: C - Humidifier 3
// Contest: AtCoder - Daiwa Securities Co. Ltd. Programming Contest 2024(AtCoder Beginner Contest 383)
// URL: https://atcoder.jp/contests/abc383/tasks/abc383_c
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;using i64 = long long;
using ui64 = unsigned long long;
using i128 = __int128;
using ui128 = unsigned __int128;
using f4 = float;
using f8 = double;
using f16 = long double;template<class T>
bool chmax(T &a, const T &b){if(a < b){ a = b; return true; }return false;
}template<class T>
bool chmin(T &a, const T &b){if(a > b){ a = b; return true; }return false;
}const int dx[] = {0, -1, 0, 1}, dy[] = {1, 0, -1, 0};signed main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int h, w, d;cin >> h >> w >> d;vector<string> a(h);for (int i = 0; i < h; i++) {cin >> a[i];}queue<tuple<int, int, int>> que;vector visit(h, vector<bool>(w, false));auto check = [&](int x, int y) {return x >= 0 && x < h && y >= 0 && y < w && a[x][y] != '#' && !visit[x][y];};auto enque = [&](int x, int y, int step) {if (check(x, y)) {que.emplace(x, y, step);visit[x][y] = true;}};for (int i = 0; i < h; i++) {for (int j = 0; j < w; j++) {if (a[i][j] == 'H') {enque(i, j, 0);}}}while (!que.empty()) {auto [x, y, step] = que.front();que.pop();if (step >= d) continue;for (int i = 0; i < 4; i++) {int nx = x + dx[i], ny = y + dy[i];enque(nx, ny, step + 1);}}int ans = 0;for (int i = 0; i < h; i++) {ans += accumulate(visit[i].begin(), visit[i].end(), 0);}cout << ans;return 0;
}
D - 9 Divisors
Description
给定 n n n,求 [ 1 , n ] [1, n] [1,n] 中正好有 9 9 9 个因数的数的数量。
1 ≤ n ≤ 1 0 12 1 \le n \le 10^{12} 1≤n≤1012
Solution
由因数个数定理知,满足条件的数 t t t只有两种可能:
- t = p 8 t=p^8 t=p8
- t = p 1 2 × p 2 2 t=p_1^2 \times p_2^2 t=p12×p22
显然 p p p 一定 ≤ n \le \sqrt{n} ≤n,所以只需筛出 n \sqrt{n} n 内的质数即可。
显然答案远小于 n \sqrt{n} n (看大样例也知道),因此枚举即可。
注意及时跳出循环(特别是情况2,否则会 TLE)
Code
// Problem: D - 9 Divisors
// Contest: AtCoder - Daiwa Securities Co. Ltd. Programming Contest 2024(AtCoder Beginner Contest 383)
// URL: https://atcoder.jp/contests/abc383/tasks/abc383_d
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;using i64 = long long;
using ui64 = unsigned long long;
using i128 = __int128;
using ui128 = unsigned __int128;
using f4 = float;
using f8 = double;
using f16 = long double;template<class T>
bool chmax(T &a, const T &b){if(a < b){ a = b; return true; }return false;
}template<class T>
bool chmin(T &a, const T &b){if(a > b){ a = b; return true; }return false;
}signed main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);i64 n;cin >> n;vector<bool> isp;vector<int> primes;auto sieve = [&](int n) {isp.assign(n + 1, true);primes.clear();isp[0] = isp[1] = false;for (int i = 2; i <= n; i++) {if (isp[i]) {primes.push_back(i);for (int j = i + i; j <= n; j += i) {isp[j] = false;}}}};int m = sqrt(n);sieve(m);int ans = 0;for (auto p : primes) {if (1LL * p * p * p * p <= m) {ans++;}else {break;}}for (int i = 0; i < primes.size(); i++) {for (int j = i + 1; j < primes.size() && 1LL * primes[i] * primes[j] <= m; j++) {ans++;}}cout << ans;return 0;
}
E - Sum of Max Matching
Description
定义 f ( s , t ) f(s,t) f(s,t) 为 s , t s,t s,t 间的最小瓶颈路。(路径上最大边权的最小值)。
给定 n n n 点 m m m 边的无向图和两个序列 a = ( a 1 , a 2 , ⋯ , a k ) a=(a_1,a_2,\cdots,a_k) a=(a1,a2,⋯,ak), b = ( b 1 , b 2 , ⋯ , b k ) b=(b_1,b_2,\cdots,b_k) b=(b1,b2,⋯,bk),重排 b b b 使得 ∑ i = 1 k f ( a i , b i ) \displaystyle \sum_{i=1}^k f(a_i,b_i) i=1∑kf(ai,bi) 最小。
Solution
关于最小瓶颈路,有一个结论:两点间的最小瓶颈路,就是最小生成树上两点间的最大边权。
据此,可以得到一个思路:
首先将每个点 u u u 看成一个集合,其中有 c n t a u cnta_u cntau 个红点和 c n t b u cntb_u cntbu 个蓝点。
然后仿照最小生成树的做法,在合并集合时,将红蓝点对配对消去,答案加上消去的点对数 × w \times w ×w。
由上面结论可知,这个方法是正确的。
Code
// Problem: E - Sum of Max Matching
// Contest: AtCoder - Daiwa Securities Co. Ltd. Programming Contest 2024(AtCoder Beginner Contest 383)
// URL: https://atcoder.jp/contests/abc383/tasks/abc383_e
// Memory Limit: 1024 MB
// Time Limit: 2500 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;using i64 = long long;
using ui64 = unsigned long long;
using i128 = __int128;
using ui128 = unsigned __int128;
using f4 = float;
using f8 = double;
using f16 = long double;template<class T>
bool chmax(T &a, const T &b){if(a < b){ a = b; return true; }return false;
}template<class T>
bool chmin(T &a, const T &b){if(a > b){ a = b; return true; }return false;
}signed main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int n, m, k;cin >> n >> m >> k;vector<array<int, 3>> edges(m);for (auto &[u, v, w] : edges) {cin >> u >> v >> w;u--, v--;}sort(edges.begin(), edges.end(), [](const array<int, 3> &a, const array<int, 3> &b) {return a[2] < b[2];});vector<int> ca(n), cb(n);for (int i = 0, x; i < k; i++) {cin >> x;x--;ca[x]++;}for (int i = 0, x; i < k; i++) {cin >> x;x--;cb[x]++;}vector<int> p(n);iota(p.begin(), p.end(), 0);auto find = [&](auto &&self, int x) -> int {if (x != p[x]) p[x] = self(self, p[x]);return p[x];};i64 ans = 0;for (auto [u, v, w] : edges) {int x = find(find, u), y = find(find, v);if (x == y) {continue;}ca[x] += ca[y];cb[x] += cb[y];int t = min(ca[x], cb[x]);ans += 1LL * t * w;ca[x] -= t;cb[x] -= t;p[y] = x;}cout << ans;return 0;
}
F - Diversity
Description
有 n n n 个物品,第 i i i 个的价格为 p i p_i pi,价值为 u i u_i ui,颜色为 c i c_i ci。
定义一种选择的价值为 ∑ u + t × k \sum u+t \times k ∑u+t×k,其中 t t t 是所选物品的不同颜色种类数, k k k 为给定常数。
你需要选择一些物品(可以不选),在所选物品总价格不超过 x x x 的前提下,求最大价值。
Solution
容易看出是 0-1背包 的变式,首先按颜色对物品分组。
设 d p i , j dp_{i,j} dpi,j 为考虑前 i i i 种颜色,总价格在 j j j 以内的最大价值。
对于第 i i i 个颜色,额外考虑从上一个颜色,即 d p i − 1 , j − p + u + k dp_{i-1,j-p}+u+k dpi−1,j−p+u+k 转移过来即可。
注意要跳过不存在的颜色。
Code
滚掉了第一维。
// Problem: F - Diversity
// Contest: AtCoder - Daiwa Securities Co. Ltd. Programming Contest 2024(AtCoder Beginner Contest 383)
// URL: https://atcoder.jp/contests/abc383/tasks/abc383_f
// Memory Limit: 1024 MB
// Time Limit: 2500 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;using i64 = long long;
using ui64 = unsigned long long;
using i128 = __int128;
using ui128 = unsigned __int128;
using f4 = float;
using f8 = double;
using f16 = long double;template<class T>
bool chmax(T &a, const T &b){if(a < b){ a = b; return true; }return false;
}template<class T>
bool chmin(T &a, const T &b){if(a > b){ a = b; return true; }return false;
}const i64 inf = 1e18;signed main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int n, v, k;cin >> n >> v >> k;vector<vector<pair<int, int>>> adj(n);for (int i = 0, p, u, c; i < n; i++) {cin >> p >> u >> c;c--;adj[c].emplace_back(p, u);}vector<i64> dp(v + 1, -inf);dp[0] = 0;for (int c = 0; c < n; c++) {if (adj[c].empty()) {continue;}vector<i64> dp2 = dp;for (auto [p, u] : adj[c]) {for (int i = v; i >= p; i--) {dp2[i] = max({dp2[i], dp2[i - p] + u, dp[i - p] + u + k});}}dp.swap(dp2);}cout << *max_element(dp.begin(), dp.end());return 0;
}
相关文章:

AtCoder Beginner Contest 383
C - Humidifier 3 Description 一个 h w h \times w hw 的网格,每个格子可能是墙、空地或者城堡。 一个格子是好的,当且仅当从至少一个城堡出发,走不超过 d d d 步能到达。(只能上下左右走,不能穿墙)&…...

20. 内置模块
一、random模块 random 模块用来创建随机数的模块。 random.random() # 随机生成一个大于0且小于1之间的小数 random.randint(a, b) # 随机生成一个大于等于a小于等于b的随机整数 random.uniform(a, b) …...
《知识拓展 · 统一建模语言UML》
📢 大家好,我是 【战神刘玉栋】,有10多年的研发经验,致力于前后端技术栈的知识沉淀和传播。 💗 🌻 CSDN入驻不久,希望大家多多支持,后续会继续提升文章质量,绝不滥竽充数…...
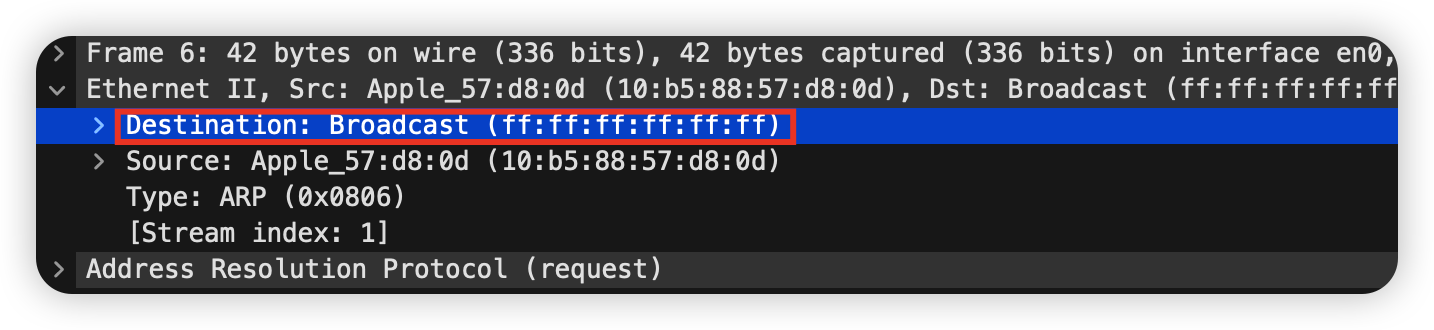
计算机网络-Wireshark探索ARP
使用工具 Wiresharkarp: To inspect and clear the cache used by the ARP protocol on your computer.curl(MacOS)ifconfig(MacOS or Linux): to inspect the state of your computer’s network interface.route/netstat: To inspect the routes used by your computer.Brows…...
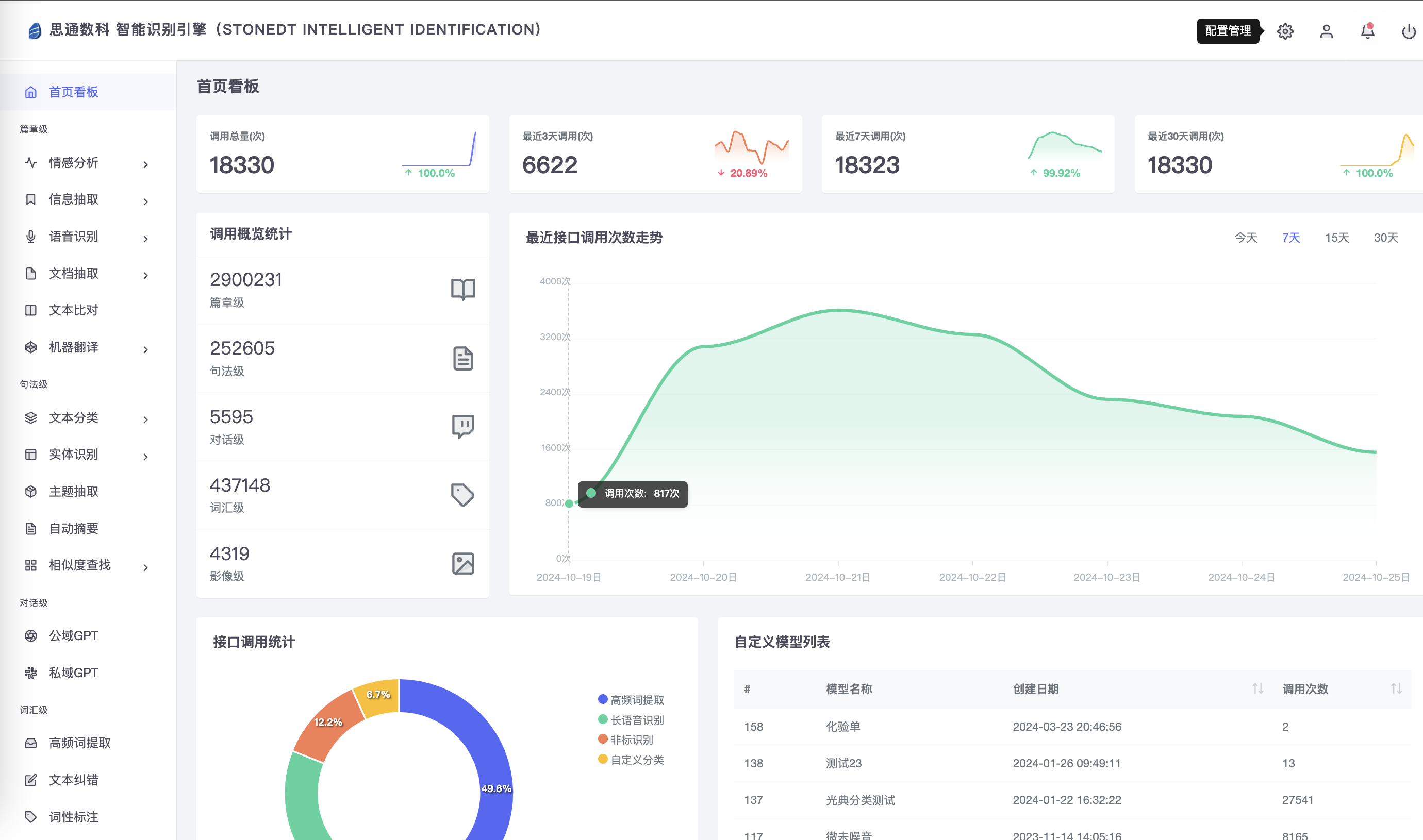
减少30%人工处理时间,AI OCR与表格识别助力医疗化验单快速处理
在医疗行业,化验单作为重要的诊断依据和数据来源,涉及大量的文字和表格信息,传统的手工输入和数据处理方式不仅繁琐,而且容易出错,给医院的运营效率和数据准确性带来较大挑战。随着人工智能技术的快速发展,…...
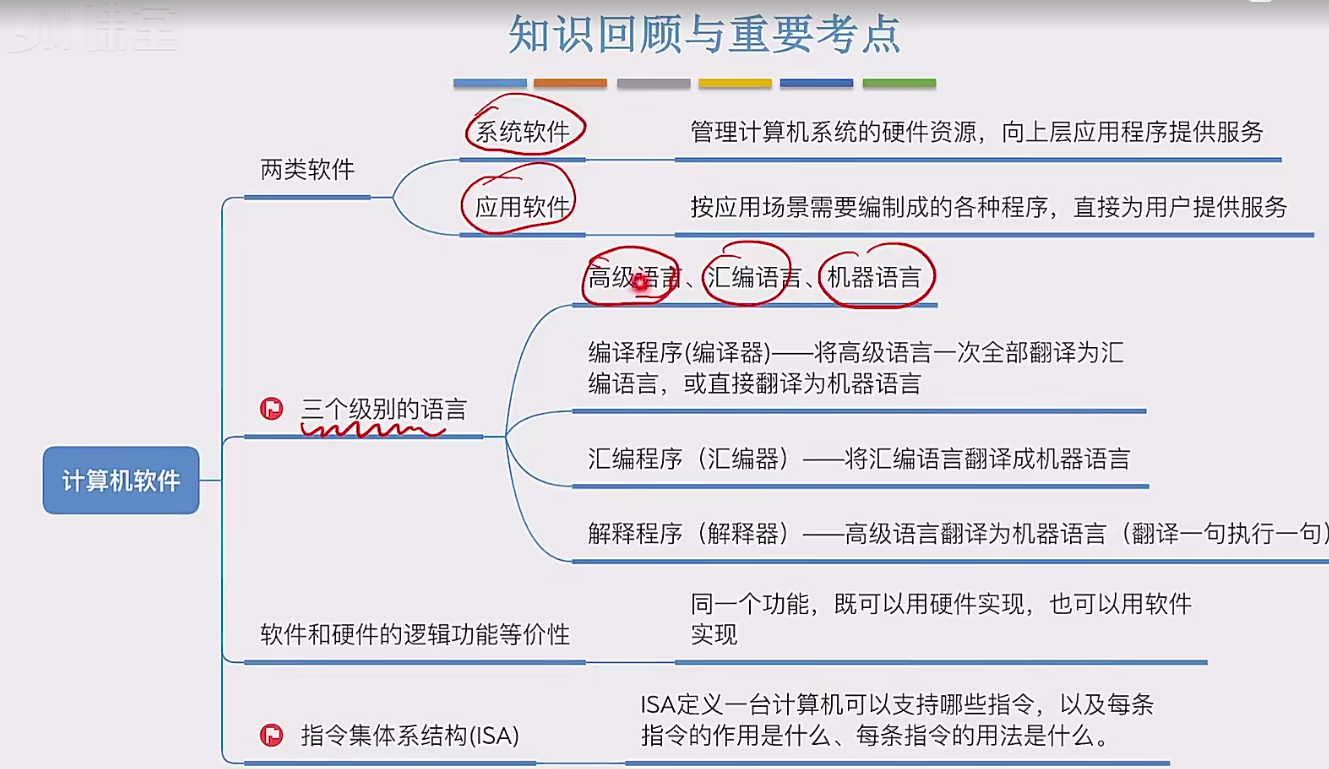
1.2.3计算机软件
一个完整的计算机系统由硬件和软件组成,用户使用软件,而软件运行在硬件之上,软件进一步的划分为两类:应用软件和系统软件。普通用户通常只会跟应用软件打交道。应用软件是为了解决用户的某种特定的需求而研发出来的。除了每个人都…...

二、uni-forms
避坑指南:uni-forms表单在uni-app中的实践经验-CSDN博客...
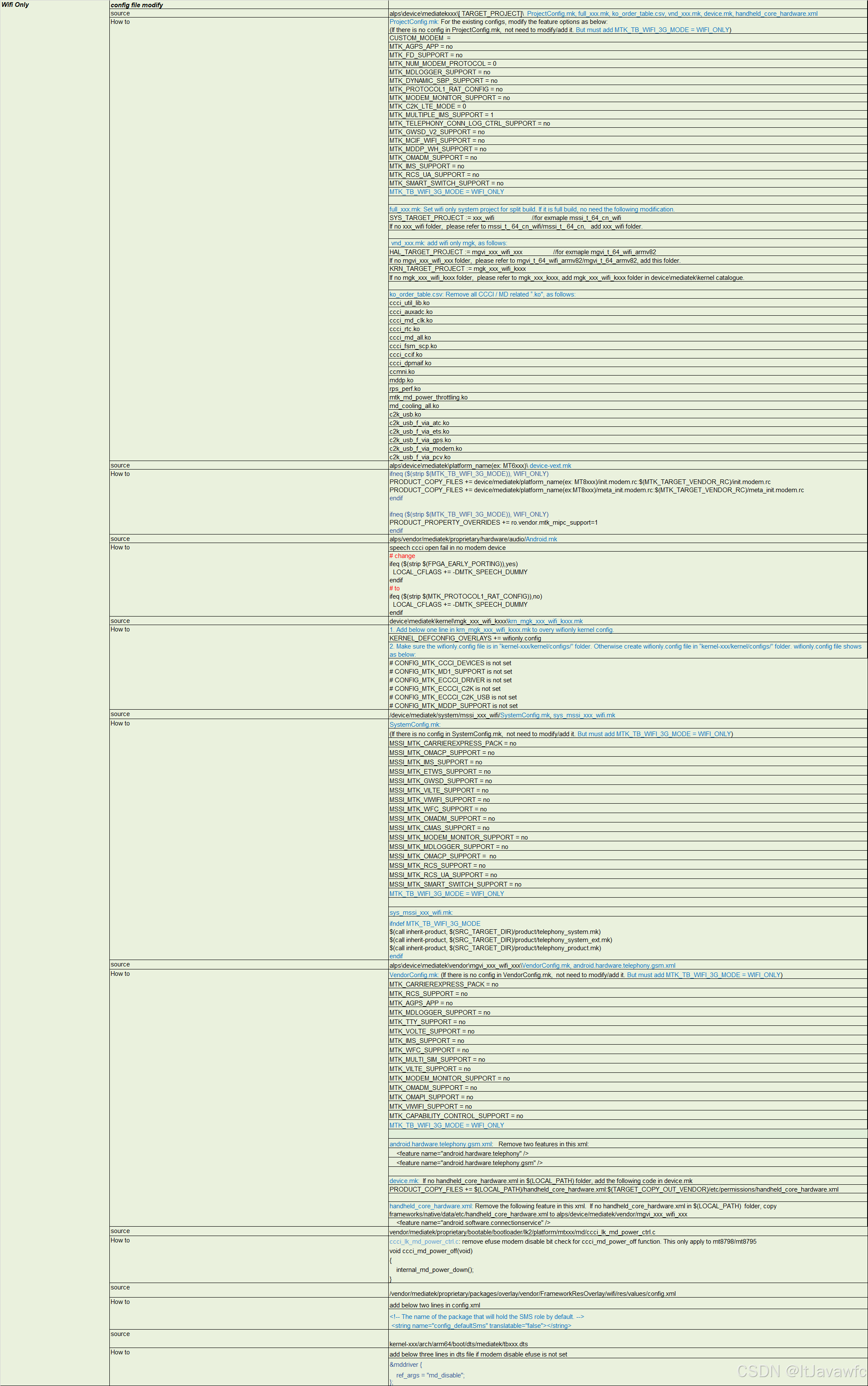
Android13开机向导
文章目录 前言需求-场景第三方资料说明需求思路按照平台 思路 从配置上去 feature换个思路,去feature。SimMissingActivity 判断跳过逻辑SetupWizardUtils 判断SIM 、 hasSystemFeature FEATURE_TELEPHONYPackageManager.FEATURE_TELEPHONYApplicationPackageManage…...

软件测试丨Appium 源码分析与定制
在本文中,我们将深入Appium的源码,探索它的底层架构、定制化使用方法和给软件测试带来的优势。我们将详细介绍这些技术如何解决实际问题,并与大家分享一些实用的案例,以帮助读者更好地理解和应用这一技术。 Appium简介 什么是App…...

1.网络知识-IP与子网掩码的关系及计算实例
IP与子网掩码 说实话,之前没有注意过,今天我打开自己的办公地电脑,看到我的网络配置如下: 我看到我的子网掩码是255.255.254.0,我就奇怪了,我经常见到的子网掩码都是255.255.255.0啊?难道公司配…...

Android中Gradle常用配置
前言 本文记录了一些常用的gradle配置,基本上都是平时开发中可能会使用到的,如果有新内容会不定时更新,附官网 1.依赖库版本写法 不推荐写法: dependencies {compile com.example.code.abc:def:2. // 不推荐的写法 }这样写虽然可…...
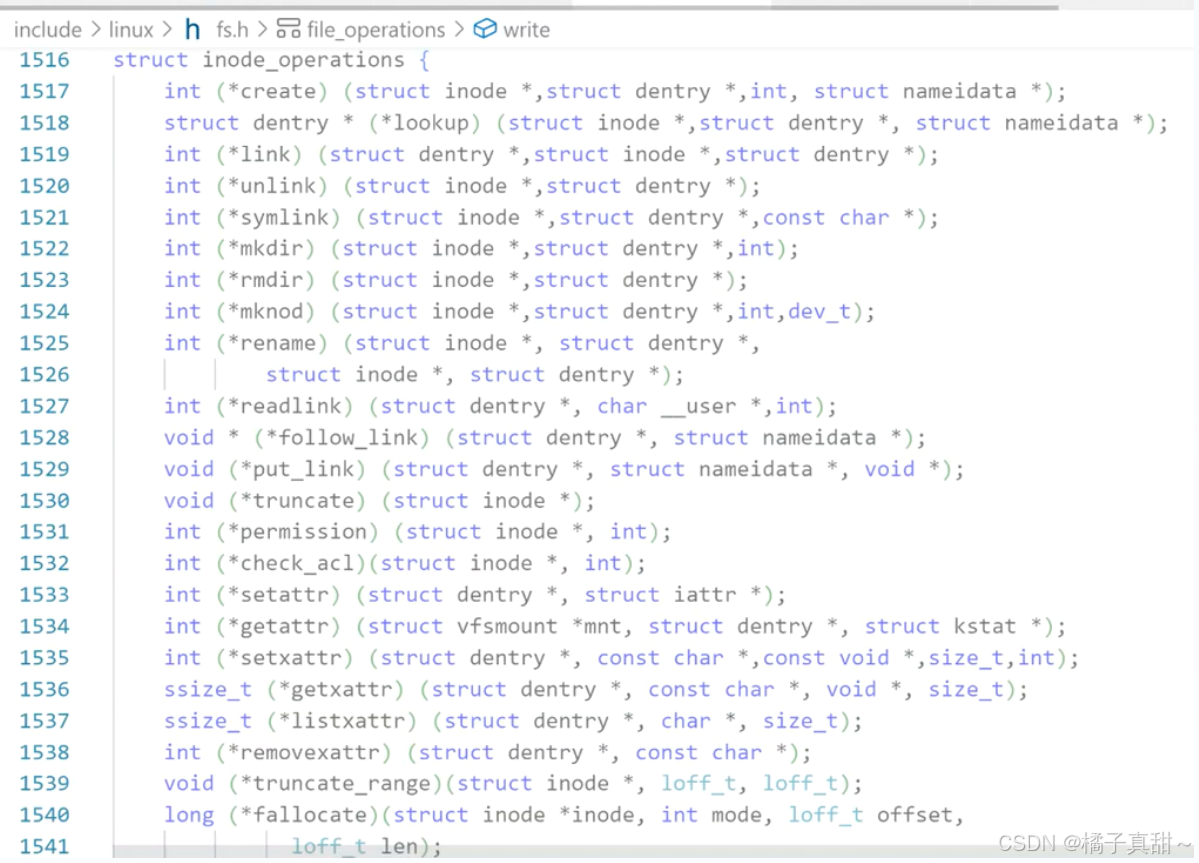
Linux操作系统3-文件与IO操作2(文件描述符fd与文件重定向)
上篇文章:Linux操作系统3-文件与IO操作1(从C语言IO操作到系统调用)-CSDN博客 本篇代码Gitee仓库:myLerningCode 橘子真甜/Linux操作系统与网络编程学习 - 码云 - 开源中国 (gitee.com) 本篇重点:文件描述符fd与文件重定向 目录 一. 文件描述…...

k8s调度策略
调度策略 binpack(装箱策略) Binpacking策略(又称装箱问题)是一种优化算法,用于将物品有效地放入容器(或“箱子”)中,使得所使用的容器数量最少,Kubernetes等集群管理系…...
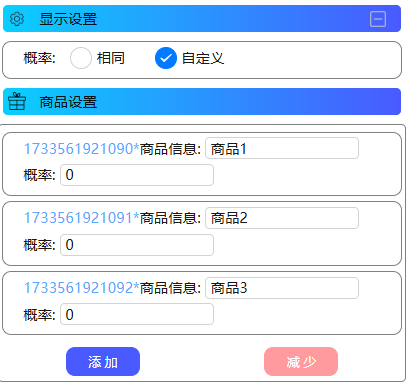
uniapp中父组件传参到子组件页面渲染不生效问题处理实战记录
上篇文件介绍了,父组件数据更新正常但是页面渲染不生效的问题,详情可以看下:uniapp中父组件数组更新后与页面渲染数组不一致实战记录 本文在此基础上由于新增需求衍生出新的问题.本文只记录一下解决思路. 下面说下新增需求方便理解场景: 商品信息设置中添加抽奖概率设置…...
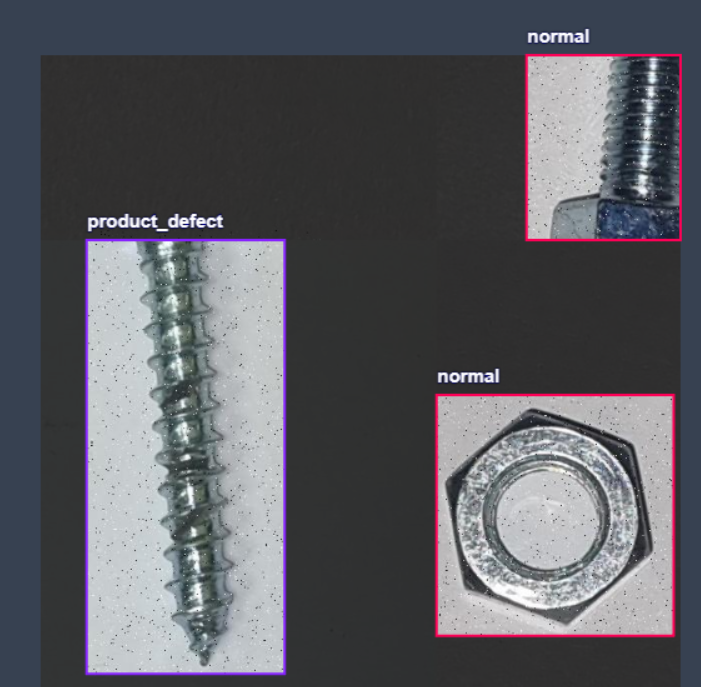
螺丝螺帽缺陷检测识别数据集,支持yolo,coco,voc三种格式的标记,一共3081张图片
螺丝螺帽缺陷检测识别数据集,支持yolo,coco,voc三种格式的标记,一共3081张图片 3081总图像数 数据集分割 训练组90% 2781图片 有效集7% 220图片 测试集3% 80图片 预处理…...
一个简单带颜色的Map
越简单 越实用。越少设计,越易懂。 需求背景: 创建方法,声明一个hashset, 元素为 {“#DE3200”, “#FA8C00”, “#027B00”, “#27B600”, “#5EB600”} 。 对应的key为 key1 、key2、key3、key4、key5。 封装该方法,…...

kubeadm安装K8s集群之基础环境配置
系列文章目录 1.kubeadm安装K8s集群之基础环境配置 2.kubeadm安装K8s集群之高可用组件keepalivednginx 3.kubeadm安装K8s集群之master节点加入 4.kubeadm安装K8s集群之worker1节点加入 kubeadm安装K8s集群基础环境配置 1.首先确保所有机器可以通信,然后配置主机host…...
前端实现在线预览excel文件
在前端开发中,经常会遇到需要在线预览各种文件的需求。本文将介绍如何使用前端技术实现在线预览 Excel 文件的功能。 一、基于微软office服务的excel预览 获取要预览的 Excel 文件的 URL(例如存储在 OneDrive 或 SharePoint 上的文件)。 使…...
关于idea-Java-servlet-Tomcat-Web开发中出现404NOT FOUND问题的解决
在做web项目时,第一次使用servlet开发链接前端和后端的操作,果不其然,遇到了诸多问题,而遇到最多的就是运行项目打开页面时出现404NOT FOUND的情况。因为这个问题我也是鼓捣了好久,上网查了许多资料才最终解决…...
SCRM私域流量管理工具助力企业微信电商转型升级
内容概要 在当今数字化时代,SCRM(社交客户关系管理)私域流量管理工具正逐渐成为企业转型的重要助力。尤其是在电商领域,企业微信的兴起为许多公司打开了新的销售渠道,通过SCRM系统的高效整合,企业能够更加…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
