红黑树(Red-Black Tree)
一、概念
红黑树(Red Black Tree)是一种自平衡的二叉搜索树,通过添加颜色信息来确保在进行插入和删除操作时,树的高度保持在对数级别,从而保证了查找、插入和删除操作的时间复杂度为 O(log n)。这种树可以很好地解决普通二叉搜索树可能退化为链表的问题。
在此文中会时不时用红黑树和AVL树作类比,朋友们可以查阅了解AVL树相关内容:AVL 树-CSDN博客
红黑树和AVL树有一些共同点:
1.平衡二叉搜索树
2.解决普通二叉搜索树在特殊情况退化为类似链表的问题
1.1红黑树的规则:
- 每个结点不是红色就是黑色
- 根结点是黑色的
- 如果一个结点是红色的,则它的两个孩子结点必须是黑色的,也就是说任意一条路径不会有连续的红色结点。
- 对于任意一个结点,从该结点到其所有NULL结点的简单路径上,均包含相同数量的黑色结点
为了大家能更快的认识和理解红黑树,看看以下的树,都是红黑树结构:

上面4棵树均是符合黑红色树规则的树。
1.2 推理
由上面4点规则推理:最长路径不超过最短路径的2倍
思考:红黑树如何确保最长路径不超过最短路径的2倍?
- 根据规则4,从根到NULL节点的每条路径都有相同数量的黑色节点。所以,在极端情况下,最短路径是全由黑色节点组成的路径,假设最短路径长度为bh(black height)。
- 根据规则2和规则3,任意一条路径不会有连续的红色节点。因此,极端情况下,最长的路径是由一黑一红交替组成的,那么最长路径的长度为2*bh。
- 结合红黑树的4点规则,理论上的全黑最短路径和一黑一红的最长路径并不会在每棵红黑树中都存在。假设任意一条从根到NULL节点的路径长度为x,那么bh ≤ h ≤ 2*bh。
说明
《算法导论》等书籍补充了一条规则,即每个叶子节点(NIL)都是黑色的。这里所指的叶子节点不是传统意义上的叶子节点,而是我们所说的空节点。一些书籍中也把NIL称为外部节点。NIL的作用是方便准确地标识所有路径。《算法导论》在后续讲解实现细节时忽略了NIL节点,因此我们只需了解这个概念即可。
1.3 红黑树的效率
假设N是红黑树中节点的数量,h是最短路径的长度,那么 2^h−1 ≤ N<2^2h−1 。由此推出 h ≈ logN 。这意味着红黑树在增删查改操作中,最坏情况下也只是走最长路径 2logN ,因此时间复杂度依然是 O(logN) 。
红黑树相对于AVL树表达更为抽象一些,AVL树通过高度差直接控制平衡。而红黑树通过四条颜色约束规则间接实现了近似平衡。虽然两者的效率同属一个档次,但在插入相同数量的节点时,红黑树的旋转次数更少,因为它对平衡的控制没那么严格。
二、红黑树节点增加与查找
2.1 红黑树插入一个值的大概过程
-
插入一个值:按二叉搜索树规则进行插入。插入后需要观察是否符合红黑树的4条规则。
-
空树插入:
-
新增结点是黑色结点。(根节点必须是黑色)
-
-
非空树插入:
-
新增结点必须是红色结点,因为插入黑色结点会破坏规则4(很难维护)。
-
如果父亲结点是黑色的,则没有违反任何规则,插入结束。
-
如果父亲结点是红色的,则违反规则2,进一步处理。
-
-
处理违反规则3:
-
c是红色,p为红,g必为黑。
-
关键看叔叔u的情况,需要根据u分为以下几种情况分别处理。
-
【说明】
下图中假设我们把新增结点标识为 (curr),c的父亲标识为 p(parent),p的父亲标识为 g(grandfather),p的兄弟标识为 u(uncle)。
情况1【变色】
-
初始状态:c为红,p为红,g为黑,u存在且为红。

-
操作:将p和u变黑,g变红。在g当做新的c,继续往上更新。
分析:
因为p和u都是红色,g是黑色。把p和u变黑,左边子树路径各增加一个黑色结点。
g再变红,相当于保持g所在子树的黑色结点的数量不变,同时解决了c和p连续红色结点的问题。
需要继续往上更新是因为 1)g是红色。如果g的父亲还是红色,那么就还需要继续处理;2)如果g的父亲是黑色,则处理结束了;3)如果g就是整棵树的根,再把g变回黑色。
情况1只变色,不旋转。所以无论c是p的左还是右,p是g的左还是右,都是上面的变色处理方式。
【图解】



可以把总的情况做成抽象图:

对照抽象图下面还有一个例子供给大家参考,可以更具象地理解向上更新的过程:


情况2【单旋 + 变色】
-
初始状态:
c为红,p为红,g为黑。u不存在或者存在且为黑。 -
如果
u不存在,则c一定是新增结点。如果u存在且为黑,则c一定不是新增结点,c之前是黑色,是在c的子树中插入,符合情况1,变色将c从黑色变成红色,更新上来的。
如图:
分析:
-
p必须变黑,才能解决连续红色结点的问题。 -
u不存在或者是黑色的,这里单纯的变色无法解决问题,需要旋转 + 变色。
旋转 + 变色(操作):
如果
p是g的左,c是p的左
- 以
g为旋转点进行右单旋。(和旋转的操作和搜索二叉树里的旋转是一样的)- 再把
p变黑,g变红即可。p变成这颗树新的根,这样子树黑色结点的数量不变,没有连续的红色结点,且不需要往上更新,因为p的父亲是黑色、红色或空都不违反规则。
如果
p是g的右,c是p的右
以
g为旋转点进行左单旋。再把
p变黑,g变红即可。
p变成这颗树新的根,这样子树黑色结点的数量不变,没有连续的红色结点,且不需要往上更新,因为p的父亲是黑色、红色或空都不违反规则。
(其实无论左边或右边操作都思路都是一种思路,这里通过文字描述给大家做参考,如果不太喜欢文字叙述可以直接看图解)
【图解】 (对应上面举例)


情况3 【双旋 + 变色】
初始状态:c 为红,p 为红,g 为黑,u 不存在或为黑色

条件分析:
如果 u 不存在 或u 存在且为黑色(与需要单旋加变色的情况二相同)
【双旋+变色】 与 【单旋+变色】对比:

双旋转 + 变色(操作):
情况1:p 是 g 的左子节点,c 是 p 的右子节点(左-右双旋)
以p为旋转点,左单旋
以g为旋转点,右单旋
变色:p 和 g 变红,将 c 变黑。
情况2:p 是 g 的右子节点,c 是 p 的左子节点(右-左双旋)
以p为旋转点,右单旋
以g为旋转点,左单旋
变色:p 和 g 变红,将 c 变黑。
【图解】 (对应上面举例)
 抽象图讨论由子树更新上来的情况:
抽象图讨论由子树更新上来的情况:


2.2红黑树节点查找
红黑树的查找操作与普通的二叉搜索树的查找操作非常相似。
都遵循相同的查找规则,即在每个节点比较查找键值和当前节点的键值,根据比较结果选择继续在左子树或右子树中查找。
【步骤】
-
从根节点开始:查找从树的根节点开始。
-
比较键值:将查找键与当前节点的键进行比较。
-
如果查找键小于当前节点的键,则继续在左子树中查找。
-
如果查找键大于当前节点的键,则继续在右子树中查找。
-
如果查找键等于当前节点的键,则查找成功,返回该节点。
-
相关文章:

红黑树(Red-Black Tree)
一、概念 红黑树(Red Black Tree)是一种自平衡的二叉搜索树,通过添加颜色信息来确保在进行插入和删除操作时,树的高度保持在对数级别,从而保证了查找、插入和删除操作的时间复杂度为 O(log n)。这种树可以很好地解决普…...

Cocos 资源加载(以Json为例)
resources 通常我们会把项目中需要动态加载的资源放在 resources 目录下,配合 resources.load 等接口动态加载。你只要传入相对 resources 的路径即可,并且路径的结尾处 不能 包含文件扩展名。 resources.load("Inf", JsonAsset, (error, ass…...

解决 IntelliJ IDEA 启动错误:插件冲突处理
引言 在使用 IntelliJ IDEA 进行开发时,我们可能会遇到各种启动错误。本文将详细介绍一种常见的错误:插件冲突,并提供解决方案。 错误背景 最近,有用户在启动 IntelliJ IDEA 时遇到了一个错误,提示信息为:…...

SQL——DQL分组聚合
分组聚合: 格式: select 聚合函数1(聚合的列),聚合函数2(聚合的列) from 表名 group by 标识列; ###若想方便分辨聚合后数据可在聚合函数前加上标识列(以标识列进行分组) 常见的聚合函数: sum(列名):求和函数 avg(列名)…...

Ripro V5日主题 v8.3 开心授权版 wordpress主题虚拟资源下载站首选主题模板
RiPro主题全新V5版本,是一个优秀且功能强大、易于管理、现代化的WordPress虚拟资源商城主题。支持首页模块化布局和WP原生小工具模块化首页可拖拽设置,让您的网站设计体验更加舒适。同时支持了高级筛选、自带会员生态系统、超全支付接口等众多功能&#…...

分布式搜索引擎之elasticsearch基本使用2
分布式搜索引擎之elasticsearch基本使用2 在分布式搜索引擎之elasticsearch基本使用1中,我们已经导入了大量数据到elasticsearch中,实现了elasticsearch的数据存储功能。但elasticsearch最擅长的还是搜索和数据分析。 所以j接下来,我们研究下…...
)
java学习-第十五章-IO流(java.io包中)
一、理解 1. 简单而言:流就是内存与存储设备之间传输数据的通道、管道。 2. 分类: (1) 按方向(以JVM虚拟机为参照物)【重点】 输入流:将中的内容读入到中。 输出流:将中的内容写入到中。 (2) 按单位: 字节流…...

企业如何实现数据从源端到消费端的全链路加工逻辑可视化?
要想实现数据加工链路的可视化,血缘图谱无疑是一个有效的工具。血缘图谱能够清晰地展示数据从产生、流转、加工到最终消费的每一个环节,帮助企业直观地理解数据之间的关联和依赖关系,轻松追溯数据来源和去向,并在数据出现问题时快…...

Toxicity of the Commons: Curating Open-Source Pre-Training Data
基本信息 📝 原文链接: https://arxiv.org/abs/2410.22587👥 作者: Catherine Arnett, Eliot Jones, Ivan P. Yamshchikov, Pierre-Carl Langlais🏷️ 关键词: toxicity filtering, language models, data curation📚 分类: 机器…...

Python 单例模式工厂模式和classmethod装饰器
前言: Python作为面向对象的语言,显然支持基本的设计模式。也具备面向对象的语言的基本封装方法:属性、方法、继承、多态等。但是,做为强大的和逐渐发展的语言,python也有很多高级的变种方法,以适应更多的…...

计算机键盘简史 | 键盘按键功能和指法
注:本篇为 “计算机键盘简史 | 键盘按键功能和指法” 相关文章合辑。 英文部分机翻未校。 The Evolution of Keyboards: From Typewriters to Tech Marvels 键盘的演变:从打字机到技术奇迹 Introduction 介绍 The keyboard has journeyed from a humb…...
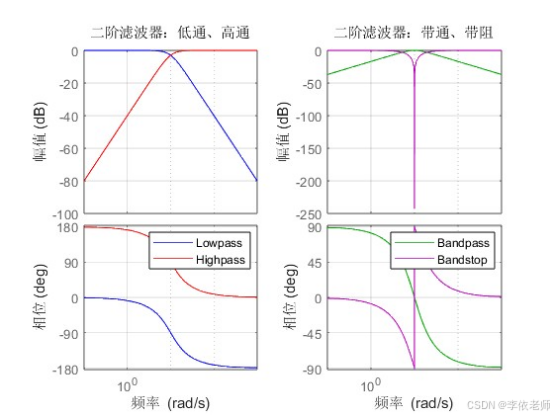
【数字信号处理】期末综合实验,离散时间信号与系统的时域分析,离散信号 Z 变换,IIR 滤波器的设计与信号滤波,用窗函数法设计 FIR 数字滤波器
关注作者了解更多 我的其他CSDN专栏 过程控制系统 工程测试技术 虚拟仪器技术 可编程控制器 工业现场总线 数字图像处理 智能控制 传感器技术 嵌入式系统 复变函数与积分变换 单片机原理 线性代数 大学物理 热工与工程流体力学 数字信号处理 光电融合集成电路…...

面试技术点之安卓篇
一、基础 二、高级 三、组件 Android中SurfaceView和TextureView有什么区别? 参考 Android中SurfaceView和TextureView有什么区别? 四、三方框架 五、系统源码 六、性能优化...
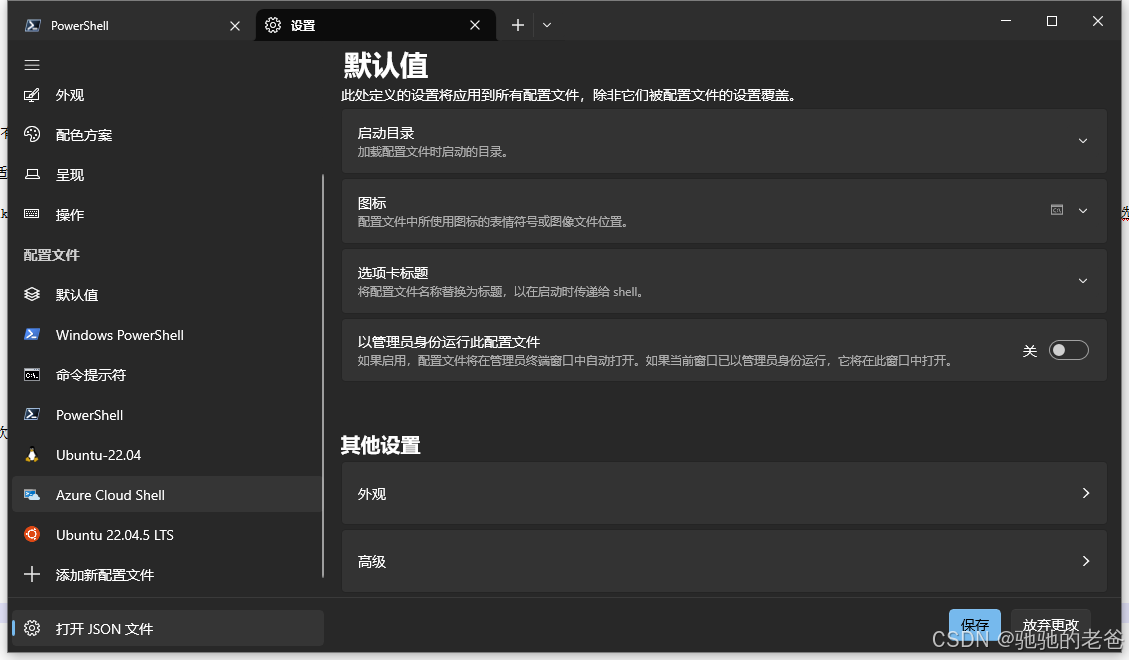
Windows Terminal ssh到linux
1. windows store安装 Windows Terminal 2. 打开json文件配置 {"$help": "https://aka.ms/terminal-documentation","$schema": "https://aka.ms/terminal-profiles-schema","actions": [{"command": {"ac…...

自适应卡尔曼滤波(包括EKF、UKF、CKF等)的创新思路——该调什么、不该调什么
在调节自适应卡尔曼滤波时,需要注意的参数和矩阵都对滤波器的性能有直接影响。本文给出详细的说明,包括相关公式和 MATLAB 代码示例 文章目录 需要调节的参数1. **过程噪声协方差矩阵 Q Q Q**:2. **测量噪声协方差矩阵 R R R**:…...
)
SpringBoot项目监听端口接受数据(NIO版)
文章目录 前言服务端相关配置核心代码 客户端 前言 环境: JDK:64位 Jdk1.8 SpringBoot:2.1.7.RELEASE 功能: 使用Java中原生的NIO监听端口接受客户端的数据,并发送数据给客户端。 服务端 相关配置 application.ym…...
QT实战--带行号的支持高亮的编辑器实现(2)
本文主要介绍了第二种实现带行号的支持高亮的编辑器的方式,基于QTextEdit实现的,支持自定义边框,背景,颜色,以及滚动条样式,支持输入变色,复制文本到里面变色,支持替换,是一个纯专业项目使用的编辑器 先上效果图: 1.头文件ContentTextEdit.h #ifndef CONTENT_TEXT_…...
网络安全书籍推荐列表)
(翻译)网络安全书籍推荐列表
注:对于所有的书籍链接,我都会寻找中文版重新链接,如无中文版,则按原文链接英文版。并且所有书籍名称保留英文名称 这是一个我建立的一个有关计算机安全的书籍列表,它们都是很有用的“计算机安全”这个主题的相关数据。…...
TcpServer 服务器优化之后,加了多线程,对心跳包进行优化
TcpServer 服务器优化之后,加了多线程,对心跳包进行优化 TcpServer.h #ifndef TCPSERVER_H #define TCPSERVER_H#include <iostream> #include <winsock2.h> #include <ws2tcpip.h> #include <vector> #include <map> #…...

黑马程序员Java项目实战《苍穹外卖》Day12
苍穹外卖-day12 课程内容 工作台Apache POI导出运营数据Excel报表 功能实现:工作台、数据导出 工作台效果图: 数据导出效果图: 在数据统计页面点击数据导出:生成Excel报表 1. 工作台 1.1 需求分析和设计 1.1.1 产品原…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...



