redis 怎么样查看list
在 Redis 中,可以通过以下方法查看列表的内容或属性:
1. 查看列表中的所有元素
使用 LRANGE 命令:
LRANGE key start end
key是列表的名称。start是起始索引,0表示第一个元素。end是结束索引,-1表示最后一个元素。
示例:
LRANGE mylist 0 -1
返回 mylist 中的所有元素。
2. 查看列表的长度
使用 LLEN 命令:
LLEN key
返回列表中元素的数量。
示例:
LLEN mylist
返回 mylist 的长度。
3. 查看列表中的特定元素
-
使用
LINDEX命令获取指定位置的元素:LINDEX key indexindex是元素的索引,0表示第一个元素,-1表示最后一个元素。
示例:
LINDEX mylist 1返回
mylist中索引为1的元素。
4. 查看列表的头部或尾部元素
-
查看头部元素:
LINDEX key 0 -
查看尾部元素:
LINDEX key -1
5. 通过命令行快速调试
在 Redis CLI 中,可以直接结合 LRANGE 和 LLEN 查看列表的内容和长度。
示例:
127.0.0.1:6379> LLEN mylist
(integer) 3
127.0.0.1:6379> LRANGE mylist 0 -1
1) "element1"
2) "element2"
3) "element3"
相关文章:

redis 怎么样查看list
在 Redis 中,可以通过以下方法查看列表的内容或属性: 1. 查看列表中的所有元素 使用 LRANGE 命令: LRANGE key start endkey 是列表的名称。start 是起始索引,0 表示第一个元素。end 是结束索引,-1 表示最后一个元素…...
,是否有其他进程正占用它?)
E: 无法获取 dpkg 前端锁 (/var/lib/dpkg/lock-frontend),是否有其他进程正占用它?
我们在使用Ubuntu系统时经常性使用sudo apt install命令安装所需要的软件库,偶尔会出现如下问题: E: 无法获得锁 /var/lib/dpkg/lock-frontend - open (11: 资源暂时不可用) E: 无法获取 dpkg 前端锁 (/var/lib/dpkg/lock-frontend),是否有其…...

创建型设计模式
一、设计模式介绍 1.设计模式是什么 设计模式是指在软件开发中,经过验证的,用于解决在特定环境下,重复出现的,特定问题的解决方案; 2.设计模式怎么来的? 满足设计原则后,慢慢迭代出来的。 3.设…...

仿iOS日历、飞书日历、Google日历的日模式
仿iOS日历、飞书日历、Google日历的日模式,24H内事件可自由上下拖动、自由拉伸。 以下是效果图: 具体实现比较简单,代码如下: import android.content.Context; import android.graphics.Canvas; import android.graphics.Color;…...
vuedraggable
官方文档:https://www.npmjs.com/package/vuedraggable 中文文档:http://www.itxst.com/vue-draggable/tutorial.html 案例下载地址: https://github.com/SortableJS/Vue.Draggable.git vuedraggablehttps://sortablejs.github.io/Vue.Dr…...

新手从事直播软件源码开发搭建经验与技巧
如果从YY或六间房的PC秀场直播间系统软件算起,直播软件已经在国内风云了至少10年了,站在用户角度提到直播系统大家基本都知道核心功能有开直播刷礼物等,那么如果站在直播软件源码开发搭建的技术角度去看呢?是不是要从需求调研分析…...

相机不动,机构动作----Hands Eyes
最近在研究 手眼标定,发现大家都需付费,搞啥子,说好的开源。。。 以相机在上固定不动,机械手为 EPSON_Robot 为例,详细的一步一步实例操作指引 EPSON_Robot 的192.168.0.1 2004 Server 详细操作步骤 1. 启动程序 运…...

Scala的导入
//导入 //(1) 创建包:在src上右键,新建软件包 //(2)填写包名:小写 //(3)在包上右键,创建类。自动加入包名 //(4)导入。import 包名.类名 //导入多个类 //import jh.yuanlixueyuan.bigdata.scala03.{A,B,C} //导入包下的所有的类 /…...

vue2中父子组件传值案例总结
在 Vue 2 中,父子组件之间的传值是通过 props 和事件来实现的。下面是详细的解释和总结: 1. 父组件向子组件传值 父组件可以通过 props 向子组件传递数据。以下是一个简单的示例: 父组件 (Parent.vue) <template><div><h1…...

功能篇:springboot中实现文件导出
### Spring Boot 中实现文件导出功能 #### 概述 在现代Web应用程序中,文件导出是一个常见的需求,允许用户将数据以特定格式(如CSV、Excel、PDF等)下载到本地。本文将详细介绍如何使用Spring Boot实现文件导出功能,并…...
)
Redis客户端(Jedis、RedisTemplate、Redisson)
1. 简介 Redis作为一个当下很火热的非关系型数据库,Java从业人员基本都离不开对Redis的使用。在Java程序中该数据库,需要借助于市面上的开源客户端,如Jedis、Spring Data Redis、Redisson,它们可以作为操作Redis非关系型数据库的桥…...

Mybatis中SQL的执行过程
文章目录 Mybatis 框架SQL执行过程数据库操作映射方式SQL的执行过程- SQL解析- SQL参数映射- SQL预编译- SQL执行- 结果映射- 事务处理- 缓存处理- 日志记录与监控 扩展#与$的区别- $ 符号- # 符号总结示例 Mybatis SQL分类- 动态 SQL- 静态 SQL静态SQL和动态SQL选择${}、#{}与…...

【数据结构——栈与队列】顺序栈的基本运算(头歌实践教学平台习题)【合集】
目录😋 任务描述 相关知识 测试说明 我的通关代码: 测试结果: 任务描述 本关任务:编写一个程序实现顺序栈的基本运算。 相关知识 为了完成本关任务,你需要掌握: 初始化栈、销毁栈、判断栈是否为空、进栈、出栈、取…...

【论文阅读】PRIS: Practical robust invertible network for image steganography
内容简介 论文标题:PRIS: Practical robust invertible network for image steganography 作者:Hang Yang, Yitian Xu∗, Xuhua Liu∗, Xiaodong Ma∗ 发表时间:2024年4月11日 Engineering Applications of Artificial Intelligence 关键…...

在Linux桌面系统普及化方面的一些建议
在推动Linux桌面系统普及化的过程中,可以考虑以下几个方案和策略: 用户友好性改进: 界面设计:提升用户界面的美观性和易用性,使其更接近或超越主流操作系统的用户体验。软件兼容性:确保常用软件(…...

LLM - 多模态大模型的开源评估工具 VLMEvalKit 部署与测试 教程
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/144353087 免责声明:本文来源于个人知识与公开资料,仅用于学术交流,欢迎讨论,不支持转载。 VLMEva…...

数据结构(Queue队列)
前言: 在计算机科学中,数据结构是构建高效算法和程序的基础,而队列(Queue)作为一种经典的线性数据结构,具有重要的地位。与栈(Stack)不同,队列遵循“先进先出”…...

Qt 图形框架下图形拖动后位置跳动问题
在使用Qt 的图形框架QGraphicsScene,QGraphicsView实现图形显示时。遇到一个很棘手的BUG。 使用的图形是自定义的QGraphicsObject的子类。 现象是将图形添加到画布上之后,用鼠标拖动图形,图形能正常改变位置,当再次用鼠标点击图…...

【Linux篇】走进Linux — 开启开源操作系统之旅
文章目录 初识Linux一.Linux的起源与发展二.Linux的特点三.Linux的应用四.Linux的发行版本 Linux环境搭建一.Linux环境的搭建方式二.购买云服务器三.使用XShell远程登陆到Linux 初识Linux 一.Linux的起源与发展 1.初始动机: Linux是一个功能强大的开源操作系统&am…...
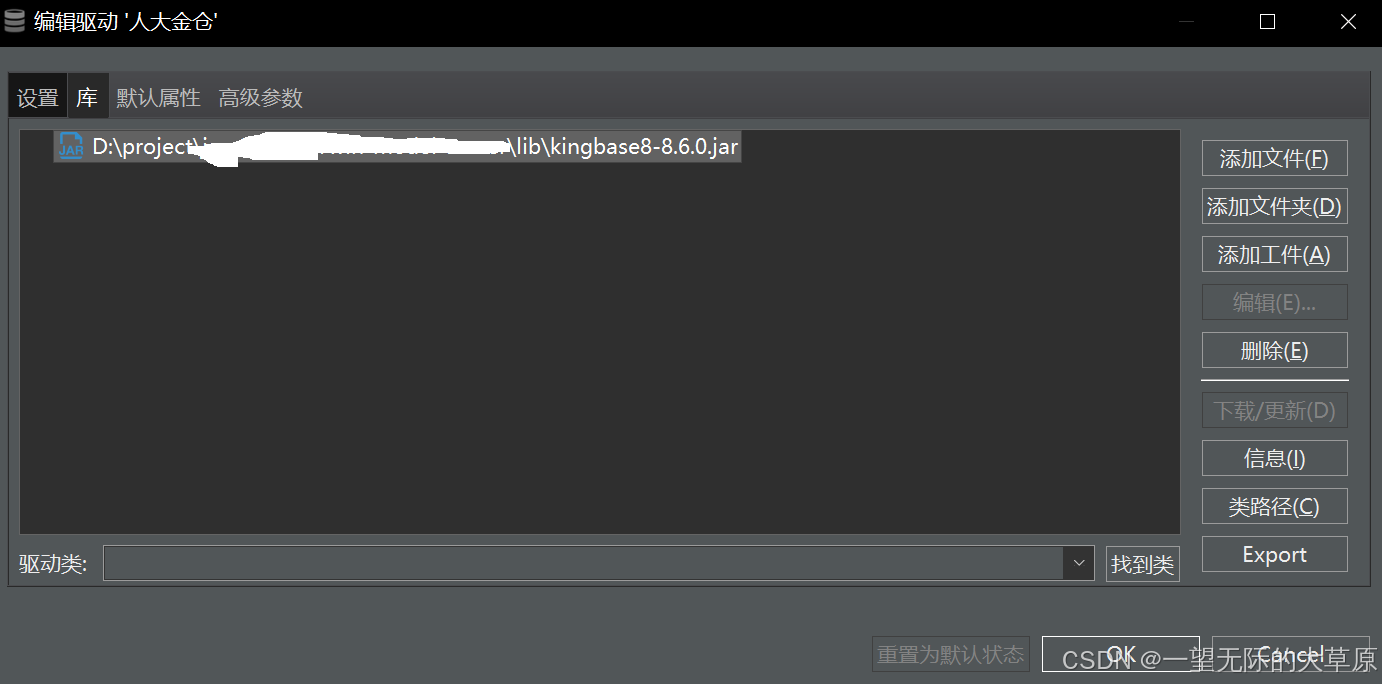
如何利用DBeaver配置连接MongoDB和人大金仓数据库
最近根据国产化要求,需要使用国产数据库,但习惯使用DBeaver连接各种成熟的商业或开源数据库。因此,就想着如何继续基于该工具,连接MongoDB和人大金仓数据库,查了半天很多地方说法不统一,所以自己就简单整理…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
