当前位置： 首页 > news >正文

【竞技宝】LOL:JDG官宣yagao离队

news 2026/2/8 22:11:43

北京时间2024年12月13日,在英雄联盟S14全球总决赛结束之后,各大赛区都已经进入了休赛期,目前休赛期也快进入尾声,LPL大部分队伍都开始陆续官宣转会期的动向,其中JDG就在近期正式官宣中单选手yagao离队,而后者大概率将直接选择退役。

近日,JDG战队在官方微博上连续发布阵容变动消息,其中就包括中单选手yagao离队的官宣微博:“经选手与俱乐部双方友好协商,在充分尊重选手个人意愿的前提下,即日起JDG京东电子竞技俱乐部中单选手曾奇(ID:Yagao)正式断开连接。光阴如梭,从最初的相遇到分别再到重聚,在无数个日夜里我们一起在赛场上携手前行,为JDG的队史里留下属于我们的故事。我们曾一起经历胜利的喜悦,也曾一同面对失利的考验,这段共同奋斗、充满欢笑与泪水的旅程之中,我们始终并肩前行,一同披荆斩棘,将它再次写入了名为JDG.Yagao的篇章之中。感谢Yagao选手一直以来为JDG京东电子竞技俱乐部的付出,同时也感谢粉丝们的支持与关注。青山一道同云雨,明月何曾是两乡。祝愿Yagao选手一切顺利,前程似锦,未来幸福快乐。”

Yagao于2016年在LDL的MSC战队开启自己的职业生涯,2017年转会加盟JDG战队之后很长时间里都效力于这支队伍,这也算得上是JDG的建队元老了。在长达8年的LPL职业生涯中,yagao取得了非常不错的联赛成绩,其中包括2018年:取得LPL夏季赛季军、全国电子竞技大赛冠军。2019年LPL春季赛亚军。2020年LPL春季赛冠军、LPL夏季赛亚军,并在英雄联盟全球总决赛中进入八强。2021年LPL夏季赛以12胜4负战绩成功晋级季后赛,止步六强。2022年取得LPL春季赛殿军、LPL夏季赛冠军、德玛西亚杯冠军。2023年取得首届英雄联盟微博杯亚军、LPL春季赛亚军、英雄联盟季中冠军赛亚军、LPL夏季赛季军、英雄联盟全球总决赛四强及德玛西亚杯亚军。但随着年龄的增大,yagao的竞技状态下滑明显,2023赛季JDG的失利也和yagao状态太差有着很大的关系。

值得一提的是,战队有选手离队时发布微博都会祝对方未来的职业生涯更好,而JDG却只是表示希望yagao未来幸福快乐。据悉,JDG的原微博最后一句是“我们赛场见”,经过修改之后才变成了“未来幸福快乐”。原因也非常简单,yagao这次离队之后会正式离开职业赛场。有yagao粉丝群的网友透露,yagao在粉丝群里已经明确表示自己不会继续打职业了,甚至不会做直播直接告别英雄联盟的圈子,从此以后过普通人的生活,最后更是用“天空不曾留下我的痕迹,但我已经飞过,有缘再见咯。”对自己的粉丝们告别。Yagao虽然一直没能拿到世界赛冠军,但此前在大赛上的表现还是非常不错的,也算是成为LPL的顶级中单了,职业生涯还算圆满,希望yagao在未来的生活中一切顺利!

相关文章：

【竞技宝】LOL:JDG官宣yagao离队

北京时间2024年12月13日,在英雄联盟S14全球总决赛结束之后,各大赛区都已经进入了休赛期,目前休赛期也快进入尾声,LPL大部分队伍都开始陆续官宣转会期的动向,其中JDG就在近期正式官宣中单选手yagao离队,而后者大概率将直接选择退役。 近日,JDG战队在官方微博上连续发布阵容变动消…...

编程日记 2024/12/14 23:10:11

双目摄像头标定方法

打开matlab 找到这个标定 将双目左右目拍的图像上传（左右目最好不少于20张） 等待即可 此时已经完成标定，左下角为反投影误差，右边为外参可视化 把这些误差大的删除即可。 点击导出 此时回到主页面，即可看到成功导出 Ca…...

编程日记 2024/12/14 23:02:03

相差不超过k的最多数，最长公共子序列(一)，排序子序列，体操队形，青蛙过河

相差不超过k的最多数 链接:相差不超过k的最多数 来源：牛客网 题目描述： 给定一个数组，选择一些数，要求选择的数中任意两数差的绝对值不超过 𝑘 。问最多能选择多少个数？ 输入描述: 第一行输入两个正整…...

编程日记 2024/12/14 22:59:00

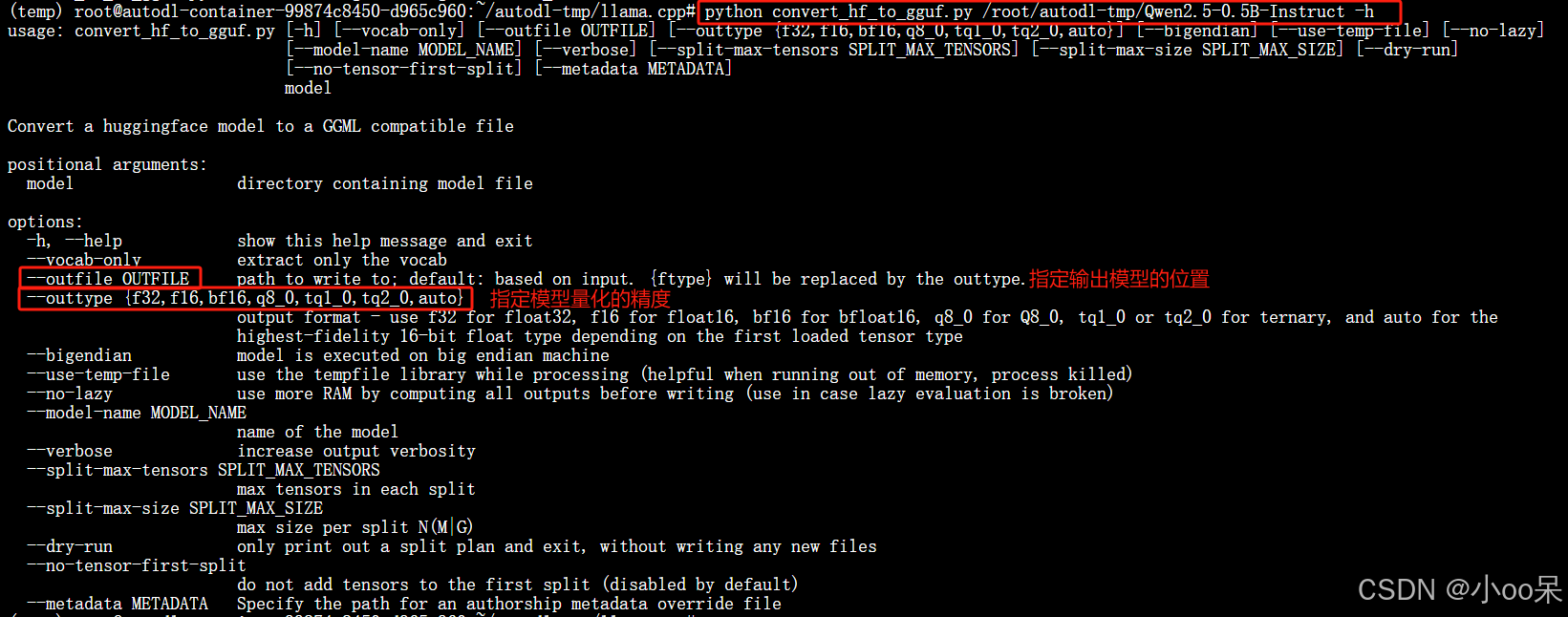
【自然语言处理与大模型】使用llama.cpp将HF格式大模型转换为GGUF格式

llama.cpp的主要目标是在本地和云端的各种硬件上以最小的设置和最先进的性能实现LLM推理。是一个专为大型语言模型（LLM）设计的高性能推理框架，完全使用C和C编写，没有外部依赖，这使得它可以很容易地被移植到不同的操作系…...

编程日记 2024/12/14 22:56:57

MongoDB存储照片和文件存储照片的区别在那里？

一、维度对比 比较维度MongoDB存储照片文件系统存储照片数据模型使用文档存储数据，可以存储不同结构的照片。以文件的形式存储照片，每个文件独立存在。性能高效的数据检索，适用于大规模应用程序中的高效检索和访问。但在处理大量高分辨率图片…...

编程日记 2024/12/14 22:49:51

协变量的概念

协变量的概念 协变量的概念 协变量（Covariate）是在统计分析和研究中，与因变量（被研究的主要变量）相关，并且可能对因变量产生影响的其他变量。它不是研究的主要关注对象，但需要在分析过程中被考虑进去，因为它可能会混淆或改变自变量与因变量之间的关系。举例说明 教育研…...

编程日记 2024/12/14 22:47:49

【[LeetCode每日一题】Leetcode 1768.交替合并字符串

Leetcode 1768.交替合并字符串 题目描述： 给定两个字符串 word1 和 word2，以交替的方式将它们合并成一个新的字符串。即，第一个字符来自 word1，第二个字符来自 word2，第三个字符来自 word1，依此类推。如果…...

编程日记 2024/12/14 22:45:47

SRT协议学习

SRT(Secure Reliable Transport)协议是一种开源的视频传输协议，旨在提供安全，可靠，低延迟的视频流传输。以下是SRT协议的一些关键的工作原理。 1 安全传输，SRT通过使用AES加密和数据完整性验证来确保数据的安全传输。它可以在不信…...

编程日记 2024/12/14 22:44:46

南昌大学《2024年837自动控制原理真题》 (完整版）

本文内容，全部选自自动化考研联盟的：《南昌大学873自控考研资料》的真题篇。后续会持续更新更多学校，更多年份的真题，记得关注哦~ 目录 2024年真题 Part1：2024年完整版真题 2024年真题...

编程日记 2024/12/14 22:39:41

ASP.NET Core 应用程序的启动与配置：Program.cs 文件的全面解析

ASP.NET Core 应用程序的启动与配置：Program.cs 文件的全面解析 Program.cs 是 ASP.NET Core 应用程序的入口点，负责应用程序的启动和配置。以下是 Program.cs 文件中完成的主要工作，按逻辑步骤进行总结： 1. 创建和配置主机环境…...

编程日记 2024/12/14 22:37:39

2020-12-02 数字过滤

缘由 C语言 数组&#xff1a;数字过滤-CSDN问答 void chuli(int n15236) {int aa[47]{0},j0,m0;while(n)aa[j]n%10,n/10;while(j)if(aa[--j]%2)m*10,maa[j];cout << m << ends; ​​​​​​​} void 数字过滤(int n 15236) {int aa[47]{0}, j 0, m 0;while (…...

编程日记 2024/12/14 22:22:23

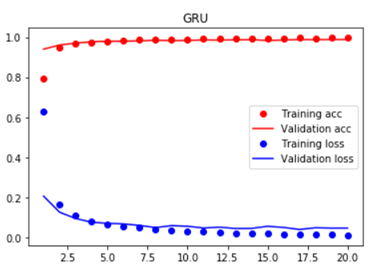
长短期记忆神经网络（LSTM）介绍

1、应用现状 长短期记忆神经网络&#xff08;LSTM&#xff09;是一种特殊的循环神经网络(RNN)。原始的RNN在训练中&#xff0c;随着训练时间的加长以及网络层数的增多&#xff0c;很容易出现梯度爆炸或者梯度消失的问题&#xff0c;导致无法处理较长序列数据&#xff0c;从而无…...

编程日记 2024/12/14 22:21:22

数据结构 ——二叉树转广义表

数据结构 ——二叉树转广义表 1、树转广义表 如下一棵树&#xff0c;转换为广义表 root(c(a()(b()()))(e(d()())(f()(j(h()())())))) (根&#xff08;左子树&#xff09;&#xff08;右子树&#xff09;) 代码实现 #include<stdio.h> #include<stdlib.h>//保存…...

编程日记 2024/12/14 22:12:12

chattts生成的音频与字幕修改完善，每段字幕对应不同颜色的视频，准备下一步插入视频。

上一节中&#xff0c;实现了先生成一个固定背景的与音频长度一致的视频&#xff0c;然后插入字幕。再合并成一个视频的方法。 但是&#xff1a;这样有点单了&#xff0c;所以&#xff1a; 1.根据字幕的长度先生成视频片断 2.在片段上加上字幕。 3.合并所有片断&#xff0c;…...

编程日记 2024/12/14 22:11:09

数据结构开始——时间复杂度和空间复杂度知识点笔记总结

好了&#xff0c;经过了漫长的时间学习c语言语法知识&#xff0c;现在我们到了数据结构的学习。 首先&#xff0c;我们得思考一下 什么是数据结构&#xff1f; 数据结构(Data Structure)是计算机存储、组织数据的方式&#xff0c;指相互之间存在一种或多种特定关系的数据元素…...

编程日记 2024/12/14 22:09:07

路由策略与策略路由

路由策略 常用有Router-Policy&#xff0c;Filter-Policy等 控制路由是否可达&#xff0c;通过修改路由条目相关参数影响流量的转发 基于控制平面&#xff0c;会影响路由表表项&#xff0c;但只能基于目地址进行策略判定&#xff0c;于路由协议相结合使用 Router-Policy …...

编程日记 2024/12/14 22:04:02

pytorch_fid 安装笔记

目录 torch安装&#xff1a; pytorch_fid安装 torch安装&#xff1a; pip install torch2.5.0 --index-url https://download.pytorch.org/whl/cu121 pytorch_fid安装 pip install pytorch_fid 安装后&#xff0c;torch也会自动安装&#xff0c;导致torch引用报错。...

编程日记 2024/12/14 22:03:01

Qt绘制仪表————附带详细说明和代码示例

文章目录 1 效果2 原理3 编码实践3.1 创建仪表属性类3.2 设置类属性3.3 绘制图案3.3.1 设置反走样3.3.2 绘制背景3.3.3 重新定义坐标原点3.3.4 绘制圆环3.3.5 绘制刻度线3.3.6 绘制刻度线上的描述值3.3.7 绘制指针3.3.8 绘制指针数值和单位3.3.9 控制指针变化 扩展福利参考 1 效…...

编程日记 2024/12/14 22:02:00

百度地图JavaScript API核心功能指引

百度地图JavaScript API是一套由JavaScript语言编写的应用程序接口&#xff0c;它能够帮助您在网站中构建功能丰富、交互性强的地图应用&#xff0c;包含了构建地图基本功能的各种接口&#xff0c;提供了诸如本地搜索、路线规划等数据服务。百度地图JavaScript API支持HTTP和HT…...

编程日记 2024/12/14 22:00:59

mp4影像和m4a音频无损合成视频方法

第一步&#xff1a;复制高清视频地址 url 第二步:打开网址粘贴复制的视频url视频下载 第三步&#xff1a;下载-影像.mp4和-音频.m4a 第四步&#xff1a;合并视频&#xff1b; 使用ffmpeg进行无损合成&#xff08;如果没有安装ffmpeg请自行下载安装下载 FFmpeg (p2hp.com)&…...

编程日记 2024/12/14 21:57:55

论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）

HoST框架核心实现方法详解 - 论文深度解读（第二部分） 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章： 论文深度解读 + 算法与代码分析（二） 作者机构： 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题： 人形机器人…...

编程新知 2026/1/20 19:54:35

Docker 运行 Kafka 带 SASL 认证教程

Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明&#xff1a;server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

编程新知 2026/1/23 4:15:03

渗透实战PortSwigger靶场-XSS Lab 14：大多数标签和属性被阻止

<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet&#xff1a; https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

编程新知 2026/1/24 13:05:24

2024年赣州旅游投资集团社会招聘笔试真

2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案，答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年，()预言了电磁波的存在，并指出…...

编程新知 2025/12/10 4:08:53

Webpack性能优化：构建速度与体积优化策略

一、构建速度优化 1、​​升级Webpack和Node.js​​ ​​优化效果​​&#xff1a;Webpack 4比Webpack 3构建时间降低60%-98%。​​原因​​&#xff1a; V8引擎优化&#xff08;for of替代forEach、Map/Set替代Object&#xff09;。默认使用更快的md4哈希算法。AST直接从Loa…...

编程新知 2025/12/26 15:05:09

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧

上周三&#xff0c;HubSpot宣布已构建与ChatGPT的深度集成&#xff0c;这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋&#xff0c;但同时也存在一些关于数据安全的担忧。 许多网络声音声称&#xff0c;这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

编程新知 2026/2/6 4:24:06

如何应对敏捷转型中的团队阻力

应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中&#xff0c;明确沟通敏捷转型目的尤为关键&#xff0c;团队成员只有清晰理解转型背后的原因和利益&#xff0c;才能降低对变化的…...

编程新知 2026/2/4 16:04:15

前端中slice和splic的区别

1. slice slice 用于从数组中提取一部分元素&#xff0c;返回一个新的数组。 特点&#xff1a; 不修改原数组&#xff1a;slice 不会改变原数组&#xff0c;而是返回一个新的数组。提取数组的部分&#xff1a;slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

编程新知 2025/11/27 20:15:13

【Veristand】Veristand环境安装教程-Linux RT / Windows

首先声明&#xff0c;此教程是针对Simulink编译模型并导入Veristand中编写的&#xff0c;同时需要注意的是老用户编译可能用的是Veristand Model Framework&#xff0c;那个是历史版本&#xff0c;且NI不会再维护&#xff0c;新版本编译支持为VeriStand Model Generation Suppo…...

编程新知 2026/2/5 20:04:55

[USACO23FEB] Bakery S

题目描述 Bessie 开了一家面包店! 在她的面包店里&#xff0c;Bessie 有一个烤箱&#xff0c;可以在 t C t_C tC​ 的时间内生产一块饼干或在 t M t_M tM​ 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC​,tM​≤109)。由于空间…...

编程新知 2026/1/10 19:08:23