Leetcode经典题13--接雨水
题目描述
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
输入输出示例
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)
解决方案:
基本思想:
1.初始化 ans = 0。
2.从左到右遍历 height:
初始化 left_max= 0,right max = 0。
从 height[0]到当前位置寻找最大值left_max = max(height[j],left_max)。
从当前位置到 height 末端寻找最大值right max= max(height[j],right max)。
ans = ans +min(left max,right max)-height[i]。
方式一:动态规划
算法思路:提前储存每个位置上所有左边柱子高度的最大值和所有右边柱子高度的最大值
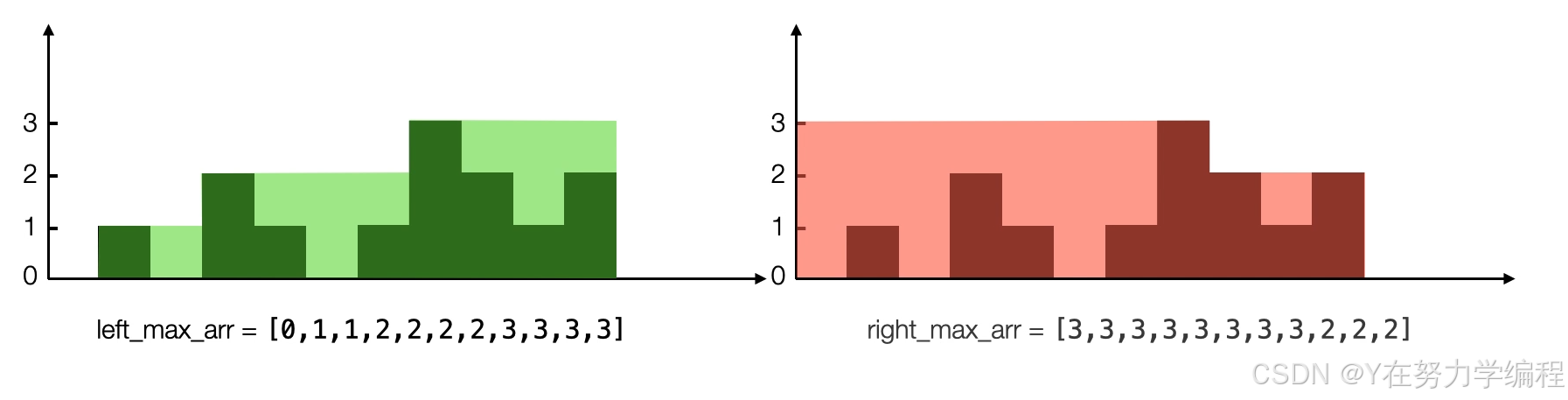
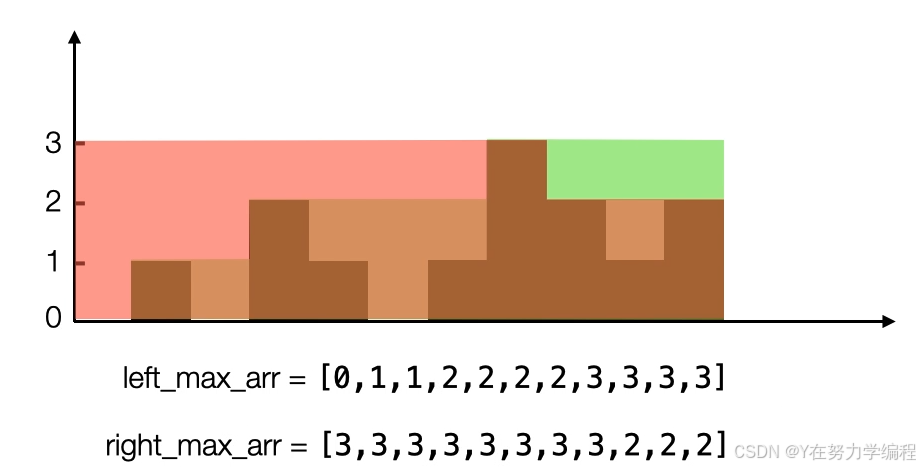
我们可以看到重叠部分,就是left_max[i]和right_max[i]之间的最小值,如果要获取存水量需要和当前的高度做差
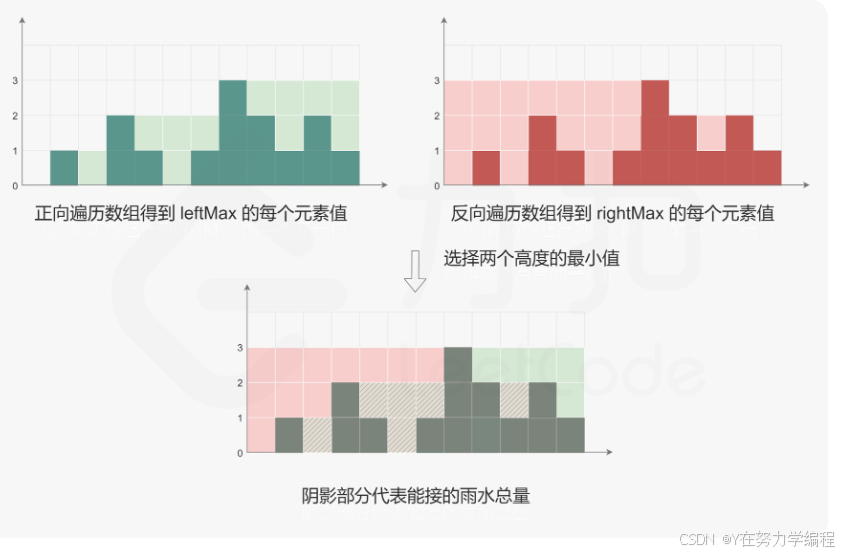
实现代码
class Solution {public int trap(int[] height) {int ans=0;//定义结果集int len=height.length;if(len<3){return 0;//这种情况下,存不住水}int[] left_max=new int[len];//每个位置上所有左边柱子高度的最大值int[] right_max=new int[len];//每个位置上所有右边柱子高度的最大值left_max[0]=height[0];right_max[len-1]=height[len-1];for(int i=1;i<len;i++){left_max[i]=Math.max(left_max[i-1],height[i]);}for(int i=len-2;i>=0;i--){right_max[i]=Math.max(right_max[i+1],height[i]);}for(int i=0;i<len;i++){ans+=Math.min(left_max[i],right_max[i])-height[i];//left_max[i]和right_max[i]之间的最小值,如果要获取存水量需要和当前的高度做差}return ans;}
}复杂度分析
时间复杂度:O(n)
其中 n 是数组 height 的长度。计算数组 leftMax 和 rightMax 的元素值各需要遍历数组 height 一次,计算能接的雨水总量还需要遍历一次。
空间复杂度:O(n)
其中 n 是数组 height 的长度。需要创建两个长度为 n 的数组 leftMax 和 rightMax。
方式二:单调栈
算法思想:积水只能在低洼处形成,当后面的柱子高度比前面的低时,是无法接雨水的。所以使用单调递减栈储存可能储水的柱子,当找到一根比前面高的柱子,就可以计算接到的雨水。
实现步骤
- 使用栈 st 来存储柱子的索引下标。
- 从左到右遍历 height:
- 当栈非空目 height[i]> height[st.peek()]。
- 意味着栈中元素可以被弹出,弹出栈顶元素。top=st.pop()
- 计算积水宽度,即当前元素和栈顶元素的距离,准备进行填充操作。distance=i-st.peek()-1
- 找出积水高度。water_height = min(height[i],height[st.peek()])- height[top]
- 往答案中累加积水量。ans += distance *bounded_height
- 将当前索引下标入栈。
- 将 i移动到下个位置。
实现代码
class Solution {public int trap(int[] height) {Stack<Integer> st=new Stack<Integer>();//使用栈 st 来存储柱子的索引下标。int i=0,ans=0;while(i<height.length){while(!st.empty()&&height[i]>height[st.peek()]){int top=st.pop();//if(st.empty()) break;int width=i-st.peek()-1;int water_height=Math.min(height[i],height[st.peek()])-height[top];ans+=width*water_height;}st.push(i++);}return ans;}
}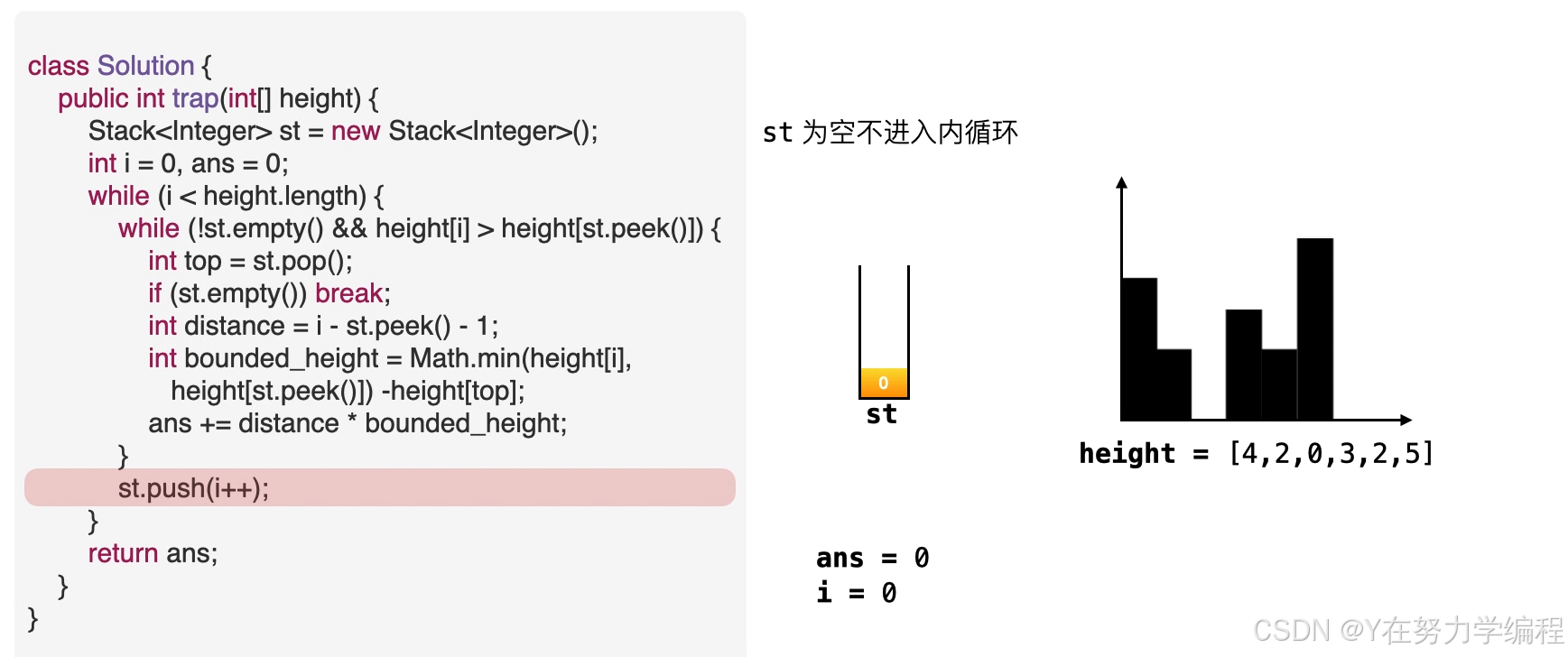
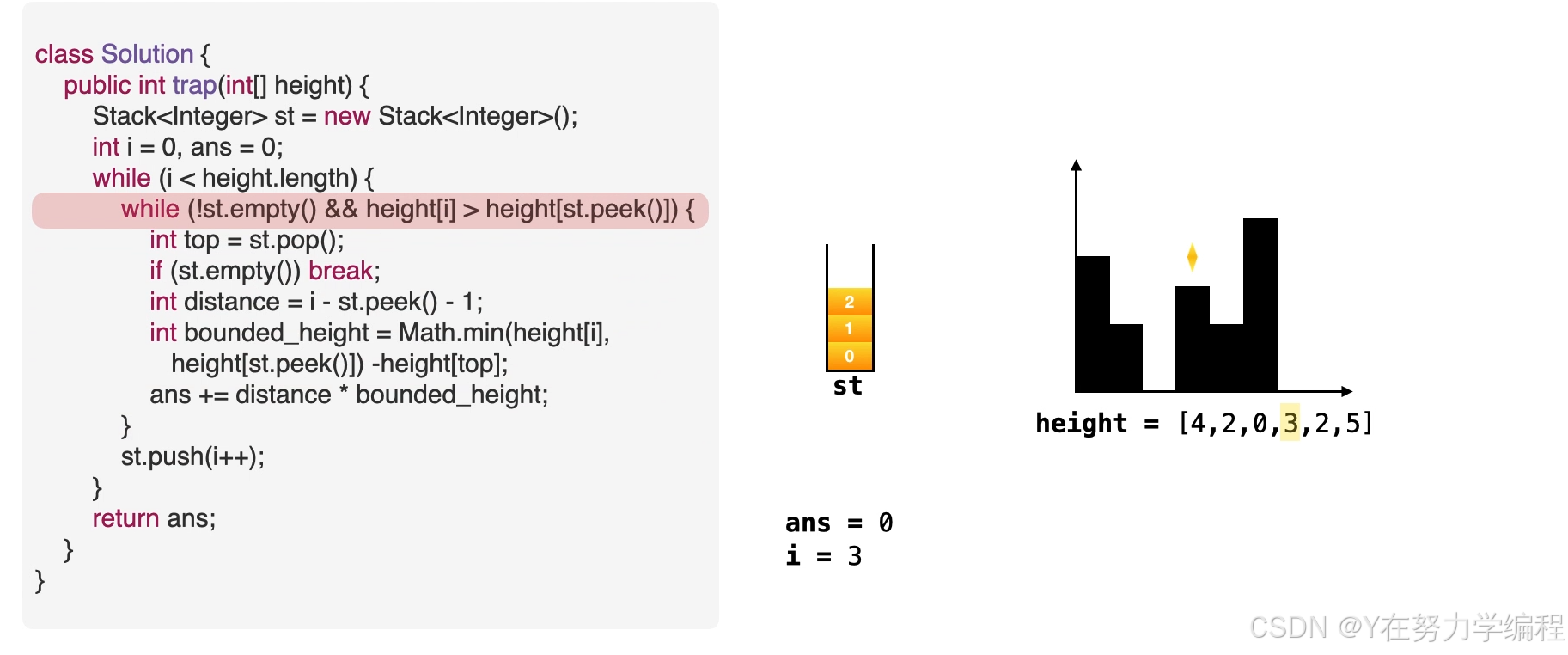
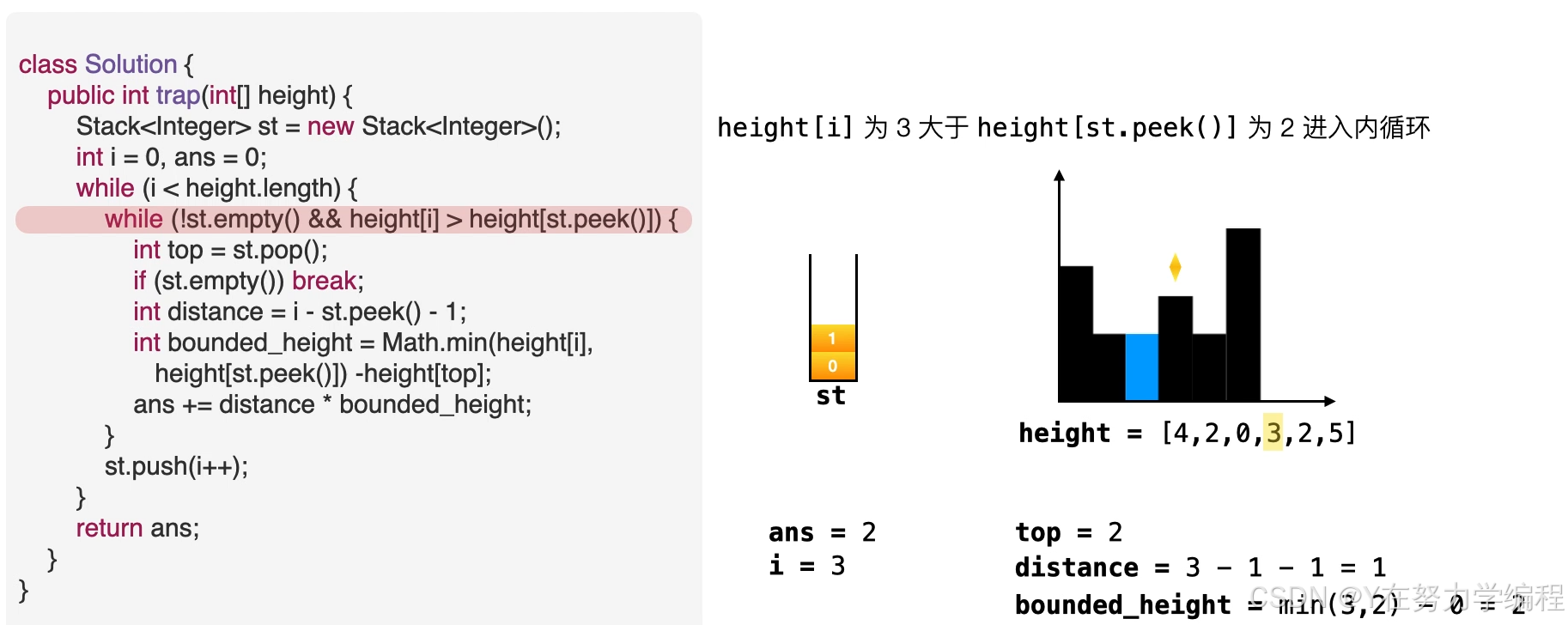
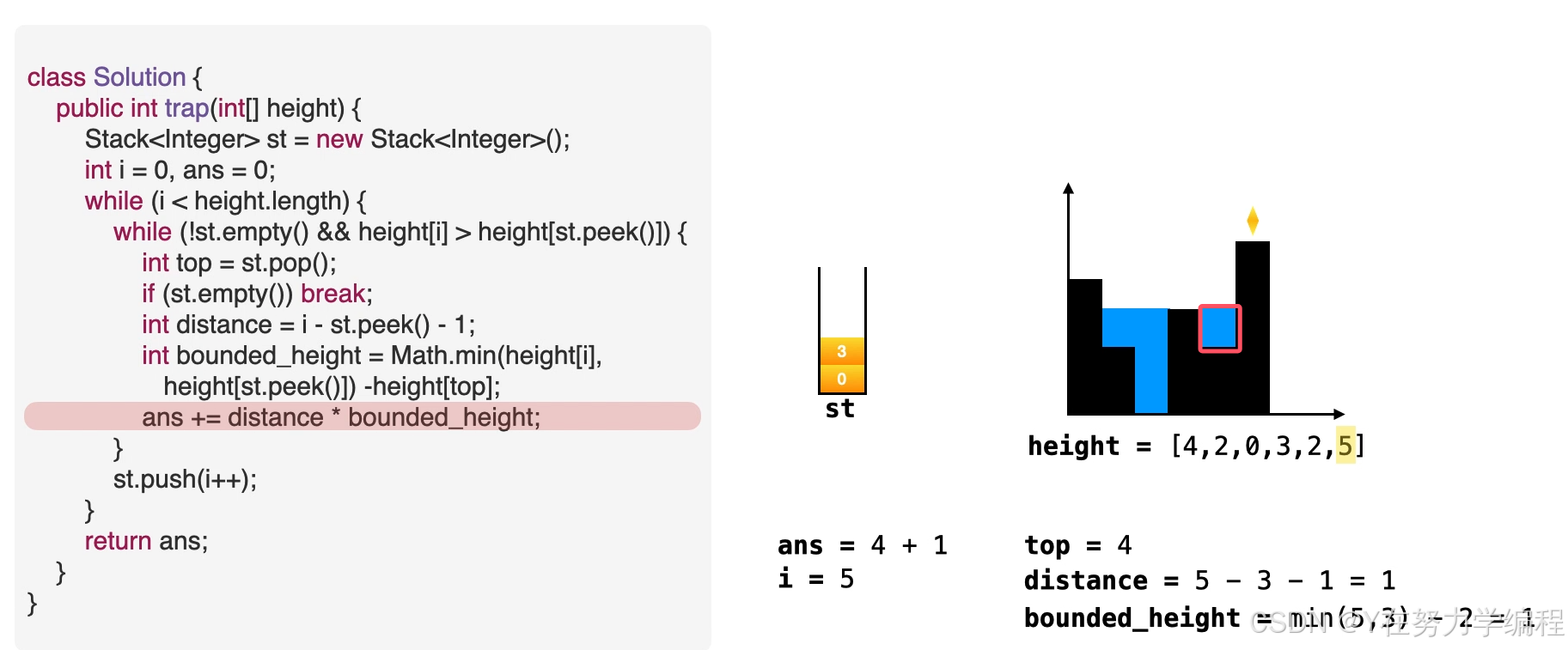
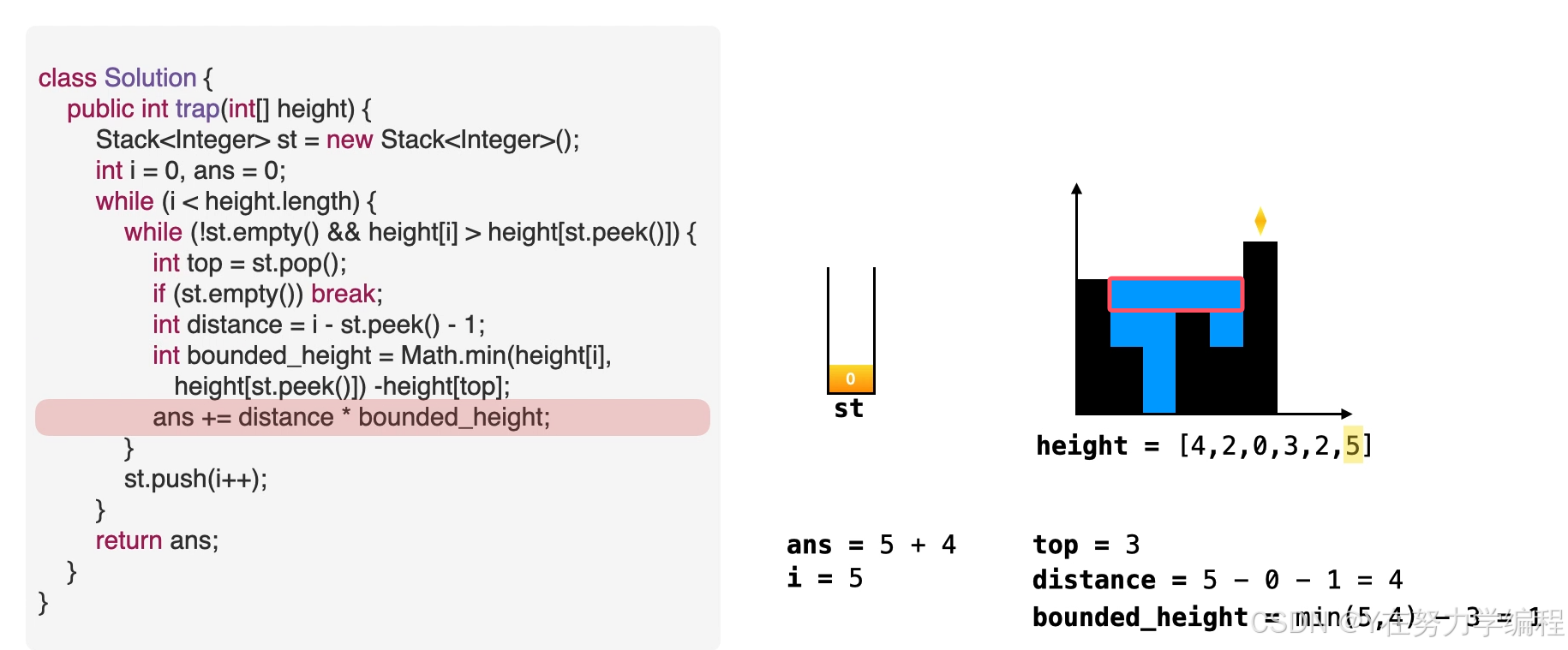
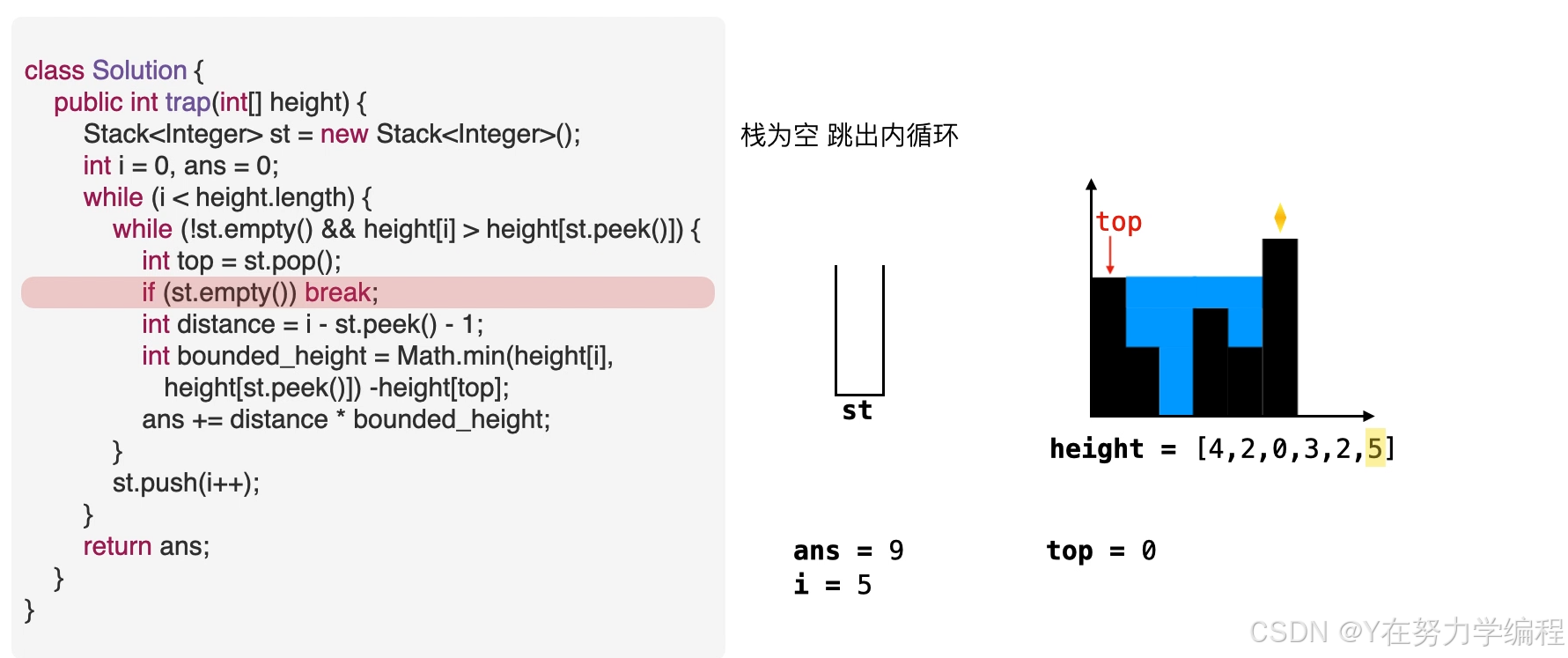
取出栈顶元素,因为是单调递减栈,所以之前的元素比栈顶元素高,当前元素也比栈顶元素高,因此在栈顶元素top会形成低洼
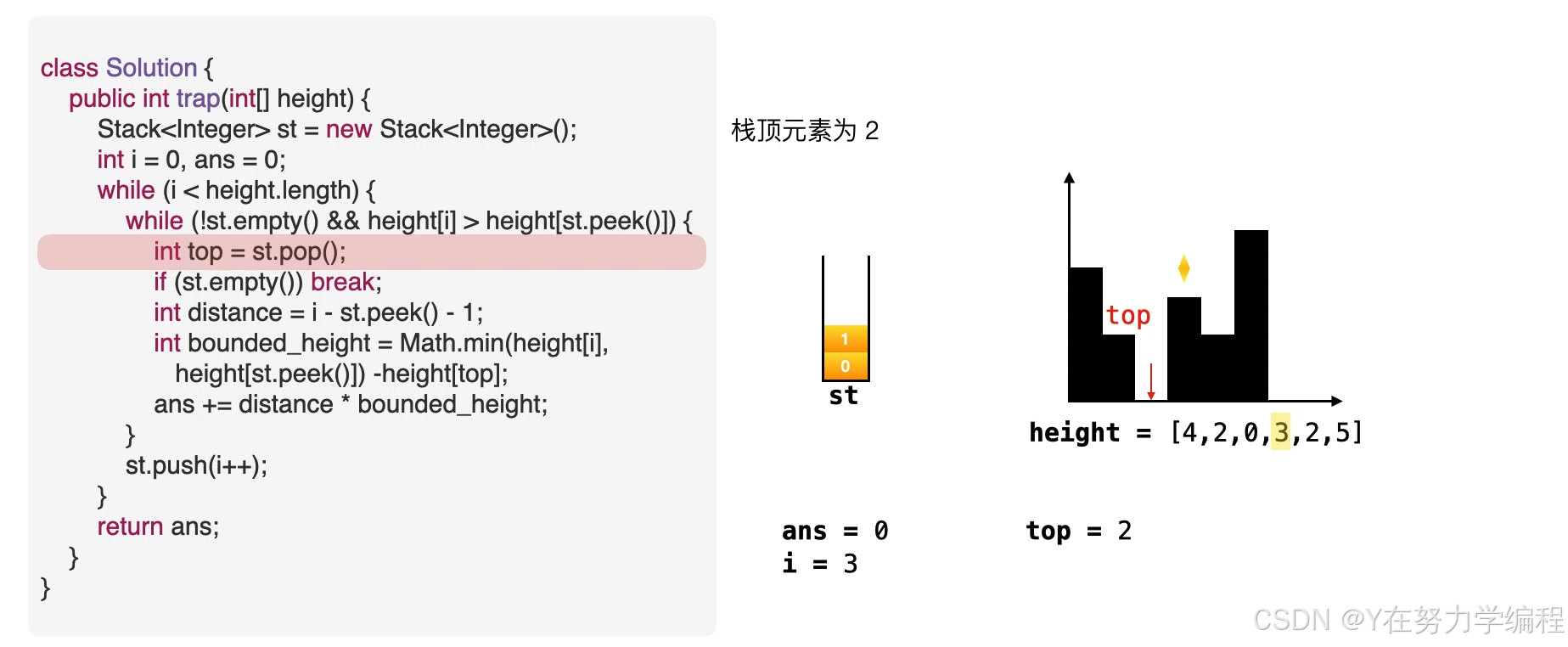
我们可以求出现在的存水量
求宽度
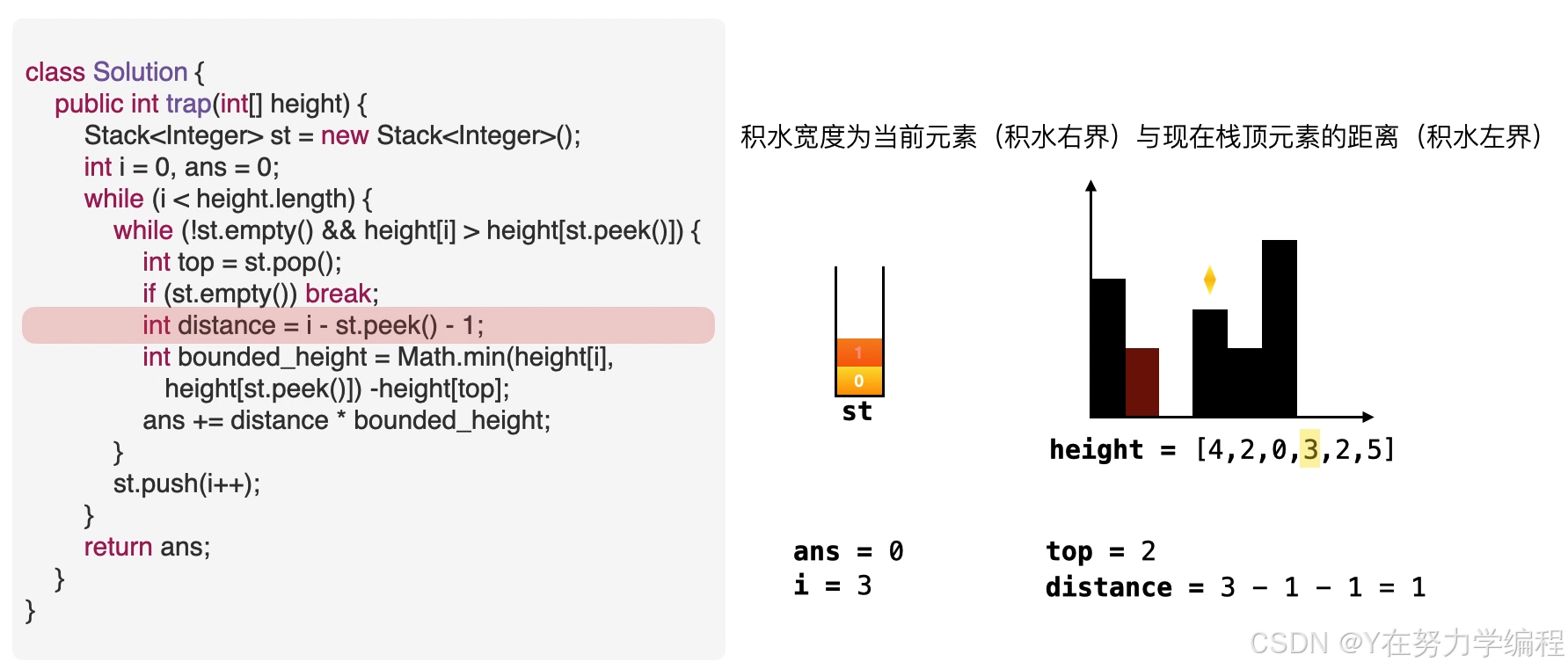
当前元素为低洼地区的右边界,而此时的栈顶元素为低洼的左边界,因而可以求出低洼处的宽度,
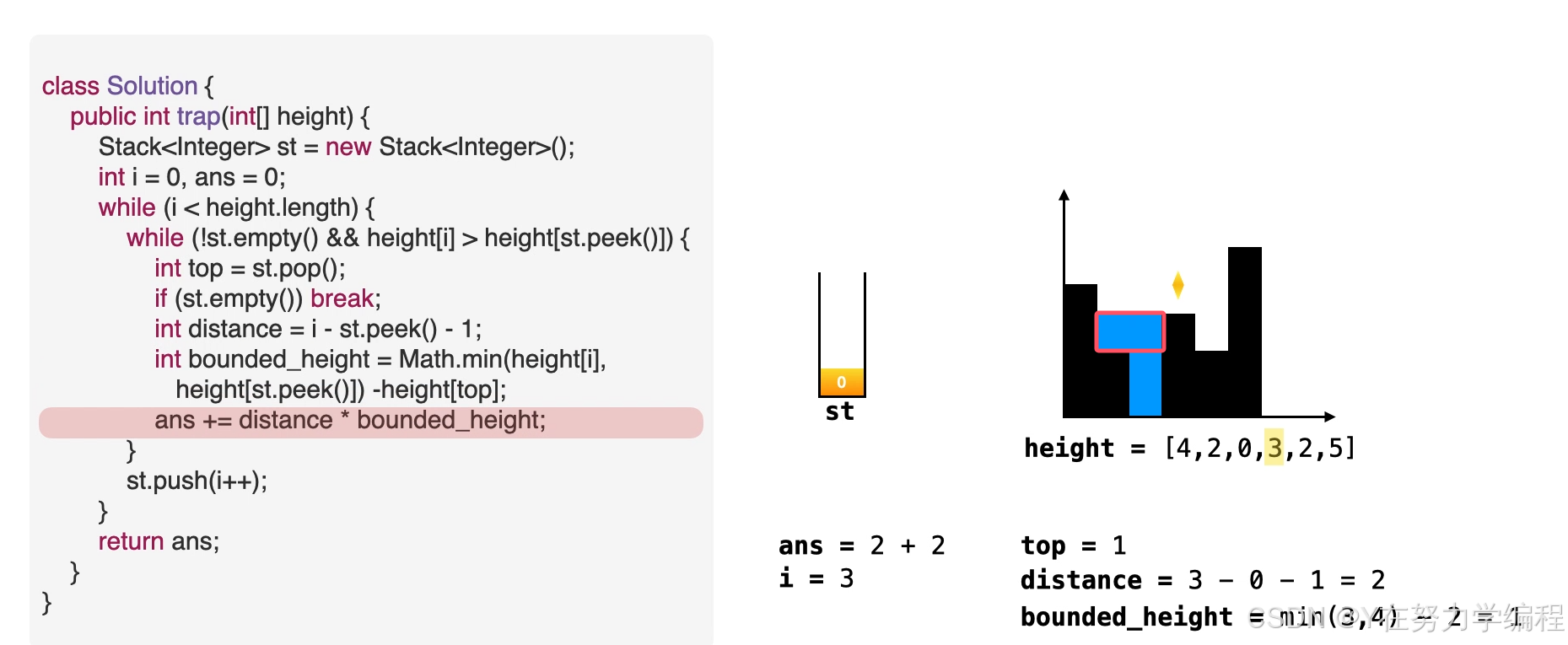
求高度

高度应为两个边界高度的较小值减去低洼处的高度
求面积
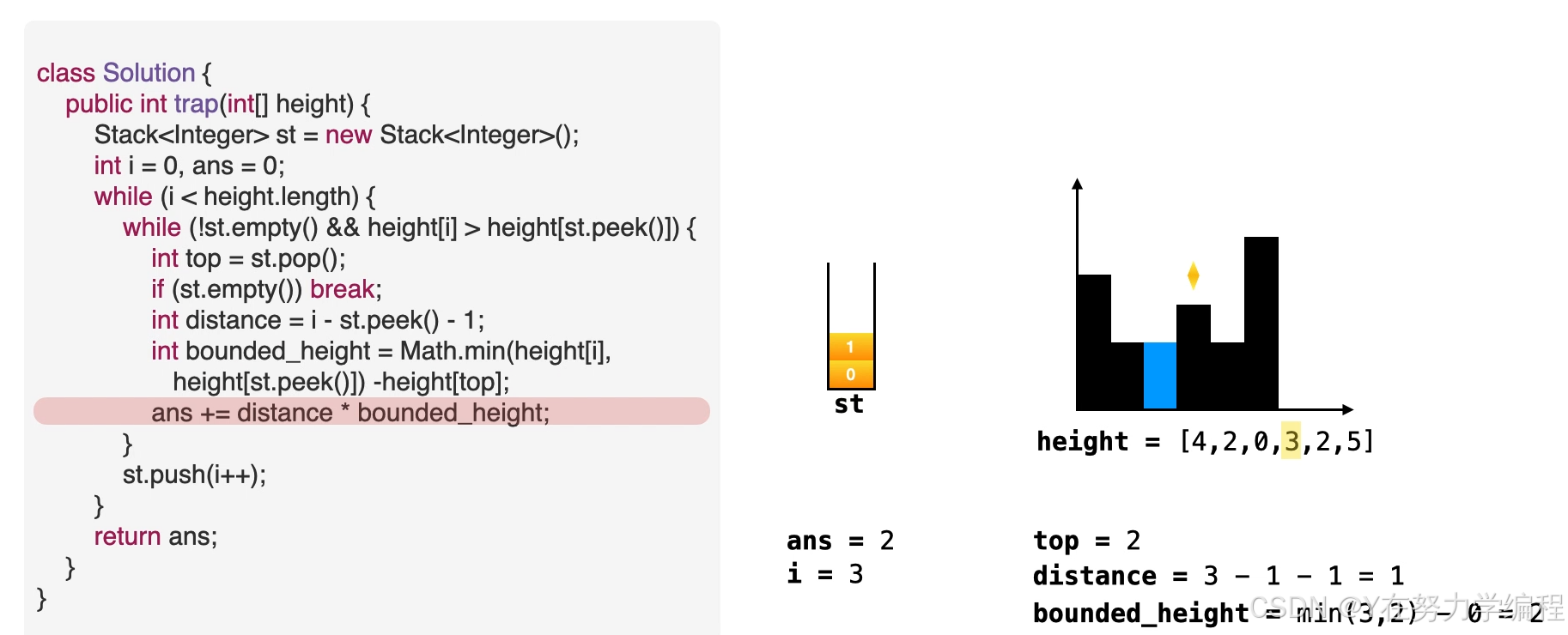
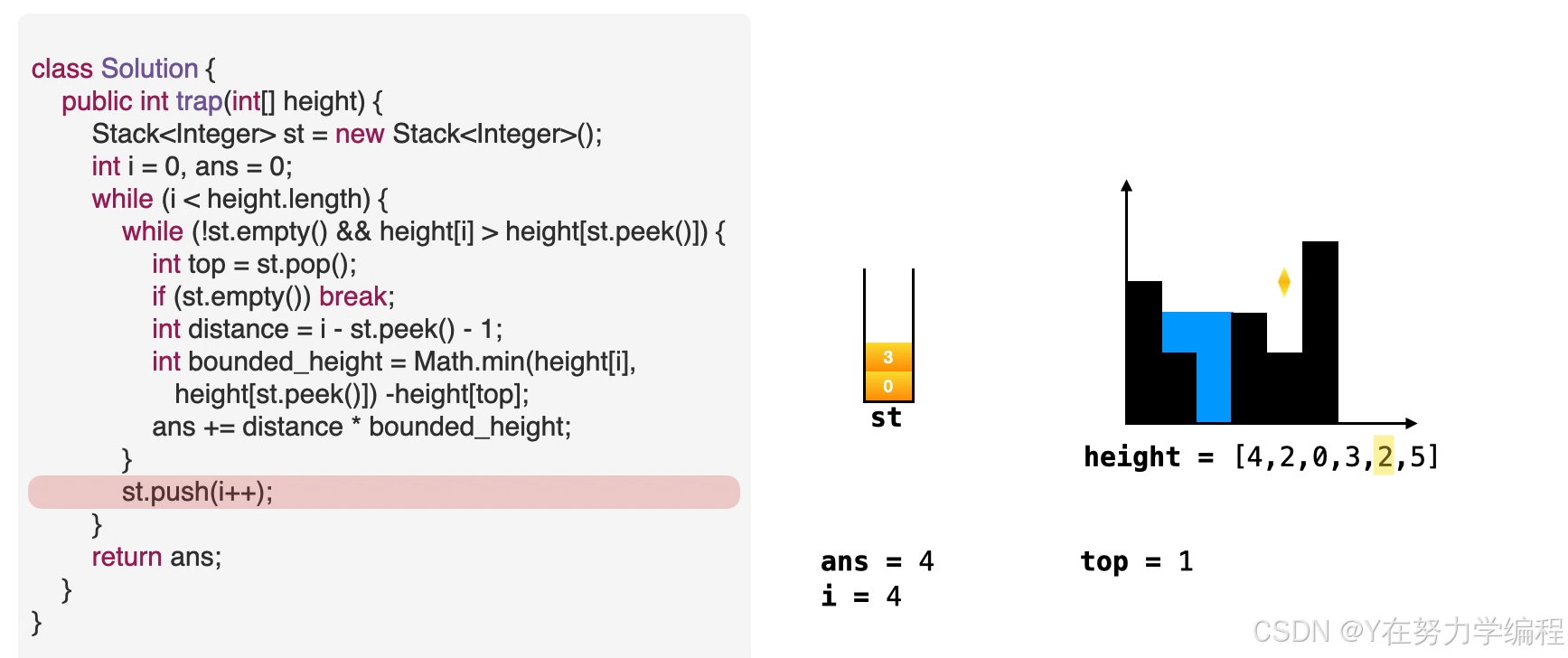
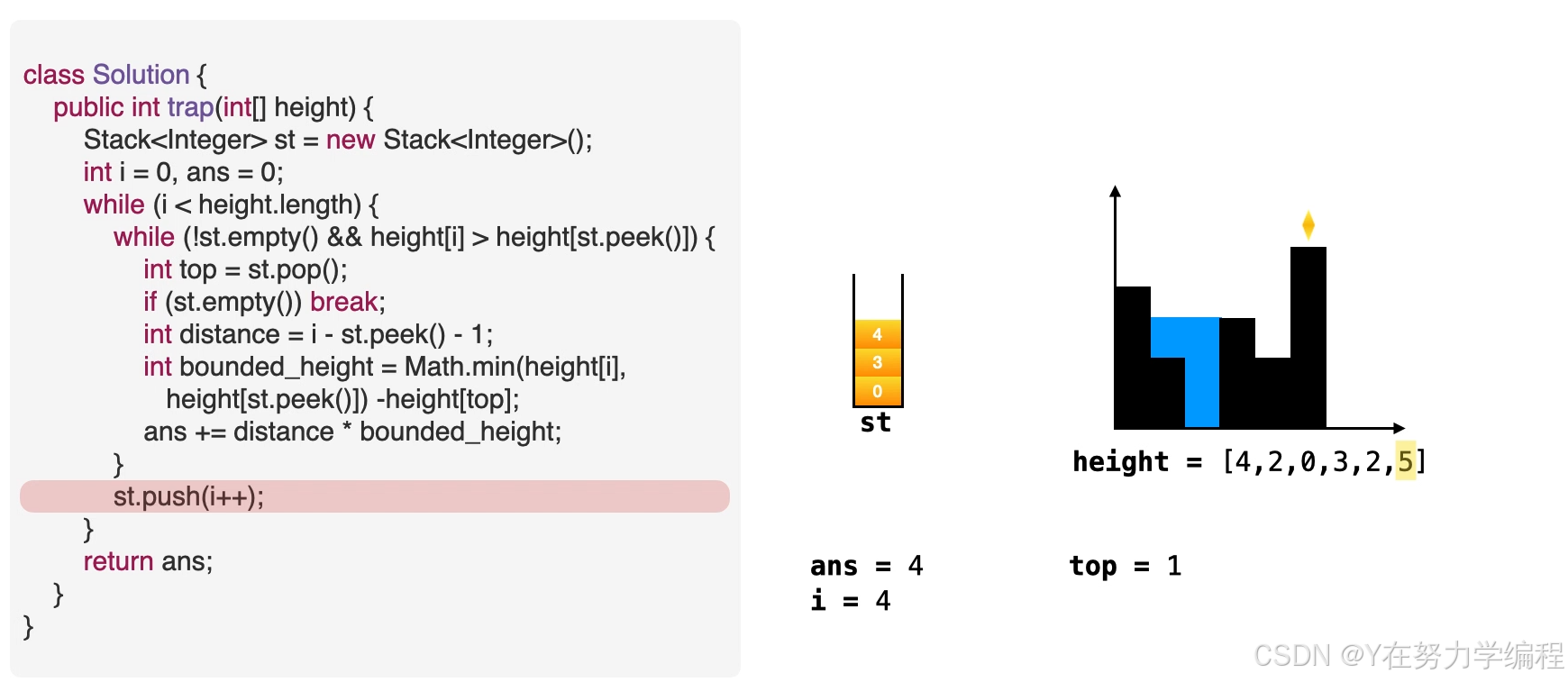
方法三: 双指针
算法思想:
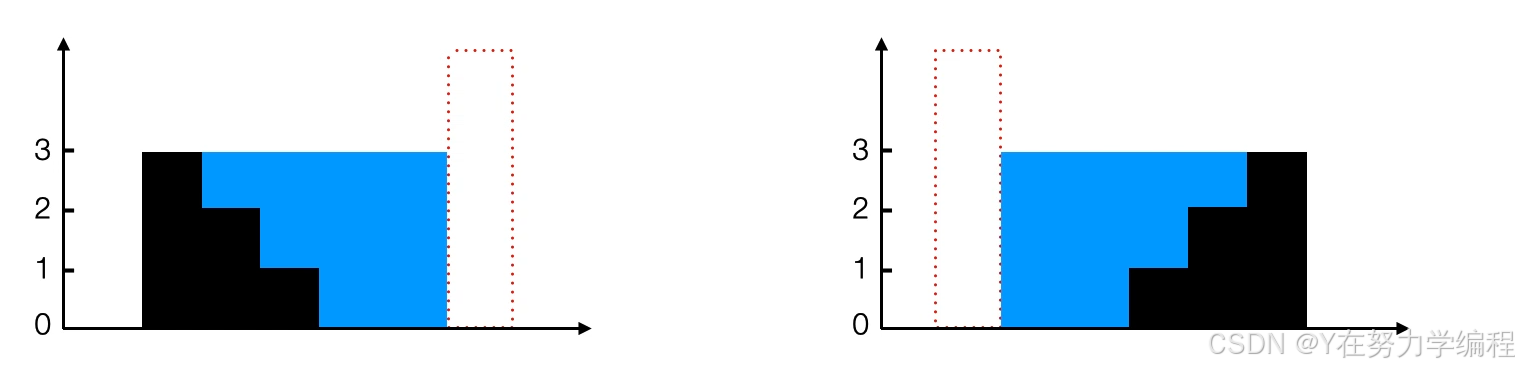
从动态规划方法的示意图中我们注意到只要 left_max[i]>right_max[i],积水的高度将由
right_max决定,同理如果 right_max[i]>left_max[i],积水的高度将由left_max决定
所以我们可以认为如果右端有更高的条形块,积水的高度依赖于当前方向的高度(从左到
右),即左边这些柱子的高度决定。当我们发现左侧有更高的条形块,我们则开始从相反的方向遍历(从右到左),即积水的高度由右边这些柱子的高度决定。
实现步骤
初始化两个指针left=0和right= height.length - 1。
当 left < right 时向中间移动两个指针:
- 如果 height [left]< height[right]说明储水量依赖于 height[left]的高度(可能构成低洼的右边界很大)
- 如果 height[left]> left max 说明没有或超出左边边界,不构成低洼,left max= height[left]。
- 如果 height[left]
- 前进 left。left ++
- 如果 height[left]>= height[right]说明储水量依赖于 height[right]的高度(可能构成低洼的左边界很大)
- 如果 height[right]> right max说明没有或超出右边边界,不构成低洼,right max= height[right]
- 如果 height[right]
- height[right]
- 前进 right。right --
实现代码:
class Solution {public int trap(int[] height) {int left=0,right=height.length-1;int left_max=0,right_max=0,ans=0;while(left<right){if(height[left]<height[right]){//高的在右边,正向遍历,找存储的if(height[left]>left_max){left_max=height[left];}else{ans+=left_max-height[left];}left++;}else{if(height[right]>right_max){right_max=height[right];//更新右侧最高点}else{ans+=right_max-height[right];}right--;}}return ans;}
}复杂度分析
时间复杂度:O(n)
其中 n 是数组 height 的长度。两个指针的移动总次数不超过 n。
空间复杂度:O(1)
只需要使用常数的额外空间。
相关文章:

Leetcode经典题13--接雨水
题目描述 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 输入输出示例 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1…...

yarn修改缓存位置
查看缓存位置 以下三个命令分别为:bin是yarn存储命令的二进制文件,global存储全局node_modules ,cache存储用下下载缓存,查看本机目前的目录: 查看bin目录命令:yarn global bin 查看global目录命令&…...

OpenHarmony-3.HDF input子系统(5)
HDF input 子系统OpenHarmony-4.0-Release 1.Input 概述 输入设备是用户与计算机系统进行人机交互的主要装置之一,是用户与计算机或者其他设备通信的桥梁。常见的输入设备有键盘、鼠标、游戏杆、触摸屏等。本文档将介绍基于 HDF_Input 模型的触摸屏器件 IC 为 GT91…...

RabbitMQ 消息持久化/镜像队列/lazy对时延影响
测试背景: 不同条件下RabbitMQ不同队列类型的生产时延测试: 测试环境: 机型:rabbimtq.2u4g.cluster 背景流量:1000 TPS 测试条件: 消息大小 4k,消息条数为1000条,时延取值为平均…...

【深度学习】深刻理解Swin Transformer
Swin Transformer 是一种基于 Transformer 的视觉模型,由 Microsoft 研究团队提出,旨在解决传统 Transformer 模型在计算机视觉任务中的高计算复杂度问题。其全称是 Shifted Window Transformer,通过引入分层架构和滑动窗口机制,S…...

[2015~2024]SmartMediaKit音视频直播技术演进之路
技术背景 2015年,因应急指挥项目需求,我们实现了RTMP推送音视频采集推送(采集摄像头和麦克风数据)模块,在我们做好了RTMP推送模块后,苦于没有一个满足我们毫秒级延迟诉求的RTMP播放器,于是第一…...

redis 使用Lettuce 当redis挂掉重启之后 网络是怎么重新连接
Lettuce是一个高性能的Java Redis客户端,支持同步、异步和反应式编程模式 Lettuce的核心功能包括: 高性能:通过使用Netty作为底层网络通信框架,实现了非阻塞IO,提高了性能。丰富的API:提供了丰富…...

【IntelliJ IDEA 集成工具】TalkX - AI编程助手
前言 在数字化时代,技术的迅猛发展给软件开发者带来了更多的挑战和机遇。为了提高技术开发群体在繁多项目中的编码效率和质量,他们需要一个强大而专业的工具来辅助开发过程,而正是为了满足这一需求,TalkX 应运而生。 一、概述 1…...

二叉搜索树Ⅲ【东北大学oj数据结构8-3】C++
二叉搜索树 III B:在二叉搜索树II中加入delete指令,创建程序对二叉搜索树T执行如下指令。 插入 k:将key k 插入到 T 中。 find k:报告T中是否存在key k。 delete k:删除key为 k 的节点。 打印:使用中序树遍…...
【面试笔记】CPU 缓存机制
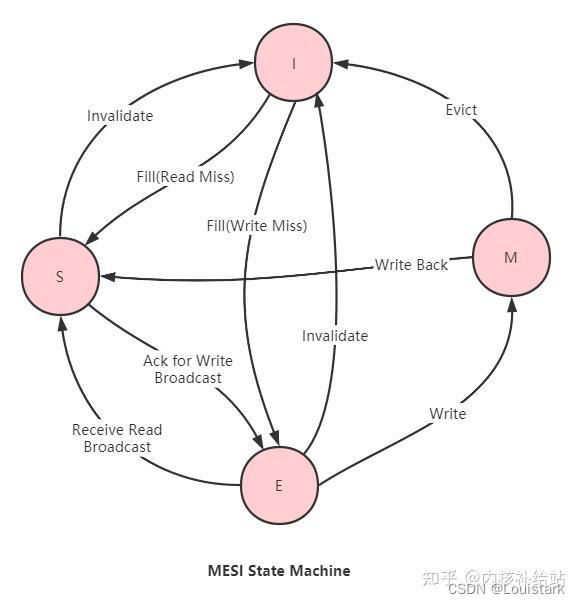
CPU 缓存机制 1. CPU Cache 与 MMU1.1 MMU 是什么?TLB 又是什么?他们是怎么工作的?2.2 简述 Cache 与 MMU 的协作关系?2.3 简述 Cache 与 MMU 的协作工作流程? 2. CPU 多层次缓存2.1 什么是 CPU 的多层次缓存结构&…...

MySQL基础函数使用
目录 简介 1. 单行函数 1.1 字符串函数 1.2 日期函数 1.3 数值函数 1.4 转换函数 1.5 其他函数 2. 多行函数 示例: 3. 数据分组 示例: 4. DQL单表关键字执行顺序 示例: 5. 多表查询 示例: 6. 表与表的外连接 示例…...

解决docker环境下aspose-words转换word成pdf后乱码问题
描述 环境:docker 部署工具:Jenkins 需求:本地上传的word文档需要转换成pdf 问题:转换之后的pdf文档出现小框框(乱码) 转换成PDF的操作 pom: <dependency><groupId>org.apach…...

C# 生成随机数的方法
C# 提供了一种强大而方便的工具类 Random ,用于生成随机数。这里将分类讨论如何通过 C# 实现随机数生成,以及应用于实际情况中的一些具体方案。 一、Random 类概述 Random 类表示一个伪随机数生成器,用于生成满足随机性统计要求的数字序列。…...

ip_done
文章目录 路由结论 IP分片 数据链路层重谈Mac地址MAC帧报头局域网的通信原理MSS,以及MAC帧对上层的影响ARP协议 1.公司是不是这样呢? 类似的要给运营商交钱,构建公司的子网,具有公司级别的入口路由器 2.为什么要这样呢?? IP地…...

3D可视化引擎HOOPS Visualize与HOOPS Luminate Bridge的功能与应用
HOOPS Visualize HPS / HOOPS Luminate Bridge为开发者提供了强大的工具,用于在CAD应用中集成逼真的渲染能力。本文旨在梳理该桥接产品的核心功能、使用方法及应用场景,为用户快速上手并充分利用产品特性提供指导。 桥接产品的核心功能概述 HOOPS Lumi…...

Docder 搭建Redis分片集群 散片插槽 数据分片 故障转移 Java连接
介绍 使多个 Redis 实例共同工作,实现数据的水平扩展。通过将数据分片到多个节点上,Redis 集群能够在不牺牲性能的前提下扩展存储容量和处理能力,从而支持更高并发的请求。Redis 集群不仅支持数据分片,还提供了自动故障转移和高可…...

校园交友app/校园资源共享小程序/校园圈子集合二手物品交易论坛、交友等综合型生活服务社交论坛
多客校园社交圈子系统搭建 校园交友多功能系统源码: 1、更改学校为独立的模块。整体UI改为绿色,青春色,更贴近校园风格。2、圈子归纳到学校去进行运营。每个学校可建立多个圈子。和其他学校圈子互不干扰。3、增加用户绑定学校,以后进入将默认…...
Chaos Mesh云原生的混沌测试平台搭建
Chaos Mesh云原生的混沌测试平台搭建 一.环境准备 确认已经安装helm,如要查看 Helm 是否已经安装,请执行如下命令: helm version二.使用helm安装 1.添加 Chaos Mesh 仓库 在 Helm 仓库中添加 Chaos Mesh 仓库: helm re…...

Vue3之组合式API详解
Vue 3引入了一种新的API风格——组合式API(Composition API),旨在提升组件的逻辑复用性和可维护性。本文将详细阐述Vue 3中的组合式API,包括其定义、特点、使用场景、优势等,并给出具体的示例代码。 一、定义 组合式…...

大模型的构建与部署(3)——数据标注
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl1. 数据标注的重要性 1.1 增强数据可解释性 数据标注通过为原始数据添加标签或注释,显著增强了数据的可解释性。在机器学习和深度学习领域,模型的训练依赖于大量带标签的数据。这些标签不仅帮助…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

