UVa 11212 Editing a Book 编辑书稿 IDA* Iterative Deepening A Star 迭代加深搜剪枝
题目链接:Editing a Book
题目描述:
给定nnn个(1<n<10)1<n<10)1<n<10)数字,数字分别是1,2,3,...,n1, 2, 3, ...,n1,2,3,...,n,但是顺序是打乱的,你可以选择一个索引区间的数字进行剪切操作。问最少进行多少次剪切可以让这nnn个数字变成升序。
例如[1,2,4,3][1, 2, 4, 3][1,2,4,3]你可以选择剪切333然后在444的前面进行粘贴操作,那么该操作算一次剪切操作序列变得升序。
题解:
对于一个含有nnn个数字的序列,要想让他变为升序,最多只需要进行nnn次剪切操作一定能让序列升序(即每次都选择未剪切过的最大的数字剪切到开头,最多进行nnn次操作,该序列一定变为有序)。那么我们可以依次枚举[0−n][0-n][0−n]表示可能的答案,每次进行暴力搜索,如果某一次枚举的时候搜索成功,那么此时枚举的次数就是最小的操作次数。这就是IDIDID算法(IterativeDeepeningIterative DeepeningIterativeDeepening迭代深搜)。因为直接搜索的话,我们每次需要枚举区间以及移动的位置,那么复杂度会达到(n3)depth(n ^3)^{depth}(n3)depth带入最大值999的话算出来的值接近6×10256\times 10^{25}6×1025很明显会超时。
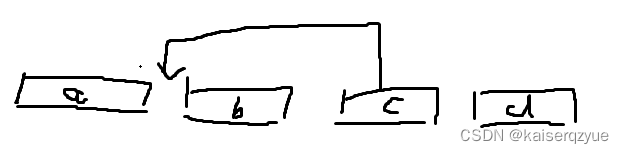
那么我们需要使用剪枝,如何进行剪枝呢?由于数字都是1−n1-n1−n的,那么我们可以记录每个数字的后一个数字不正确的个数即计算有多少个iii满足:a[i]+1]≠a[i+1]a[i] + 1] \ne a[i +1]a[i]+1]=a[i+1],我们将这个数字记为cntcntcnt,我们可以发现我们每一次剪切操作最多让cntcntcnt减少333。从下图我们可以看到如果我们进行一次剪切(下图中是把part c移到到part b的前面),后一个数字发生变化的位置有:a的最后一个元素,c的最后一个元素,b的最后一个元素。 也就是说在这种情况想最多只有三个数字的后一个元素会发生改变,当然其他情况也是可以同理推出来的。所以每一次剪切操作最多能够让cntcntcnt减少333,如果剩余的剪切操作在最优的情况下不能让cntcntcnt小于000,那么此时就应该停止搜索即:(maxDepth−nowDepth)∗3<cnt(maxDepth - nowDepth) * 3 < cnt(maxDepth−nowDepth)∗3<cnt。这也就是AstarA\ starA star算法的思想,三部分合起来就叫做IDA∗IDA*IDA∗。
实际上仅仅有上面的剪枝策略还是容易发生超时。而此时需要利用另外一种“贪心”策略:连续的升序区间不应该被执行剪切操作,也就是说对于一个序列里面类似于[2,3,4,5][2, 3, 4, 5][2,3,4,5]的序列只能作为整体操作,而不应该只剪切其中的一部分。这似乎是显然的。
代码:
#include <bits/stdc++.h>using namespace std;int n, caseID = 1;
vector<int> number;int getCnt()
{int cnt = 0;for (int i = 0; i < n - 1; i++) {if (number[i] + 1 != number[i + 1]) { cnt++; }}return cnt;
}bool dfs(int nowDepth, int maxDepth)
{int cnt = getCnt();if (nowDepth == maxDepth) { return cnt == 0; }if ((maxDepth - nowDepth) * 3 < cnt) { return false; }for (int l = 0; l < n; l++) {if (l - 1 >= 0 && number[l] - 1 == number[l - 1]) { continue; }for (int r = l; r < n; r++) { // 枚举需要移动的区间的左右端点if (r + 1 < n && number[r] + 1 == number[r + 1]) { continue; }for (int k = r + 2; k <= n; k++) { // 枚举将区间移动到k前面vector<int> temp(number);vector<int> worker;for (int i = 0; i <= k - 1; i++) { // [0, k-1]移动if (l <= i && i <= r) { continue; }worker.push_back(number[i]);}for (int i = l; i <= r; i++) { worker.push_back(number[i]); } // [l, r]移动for (int i = k; i < n; i++) { worker.push_back(number[i]); } // 剩下部分移动number.swap(worker);if (dfs(nowDepth + 1, maxDepth)) { return true; };number.swap(temp);}}}return false;
}int main()
{ios::sync_with_stdio(false);while(cin >> n && n != 0) {number.resize(n);for (int i = 0; i < n; i++) { cin >> number[i]; }for (int maxDepth = 0; ; maxDepth++) {if (dfs(0, maxDepth)) {cout << "Case " << caseID << ": " << maxDepth << endl;caseID++;break;}}}return 0;
}
相关文章:
UVa 11212 Editing a Book 编辑书稿 IDA* Iterative Deepening A Star 迭代加深搜剪枝
题目链接:Editing a Book 题目描述: 给定nnn个(1<n<10)1<n<10)1<n<10)数字,数字分别是1,2,3,...,n1, 2, 3, ...,n1,2,3,...,n,但是顺序是打乱的,你可以选择一个索引区间的数字进行剪切操作。问最少进…...
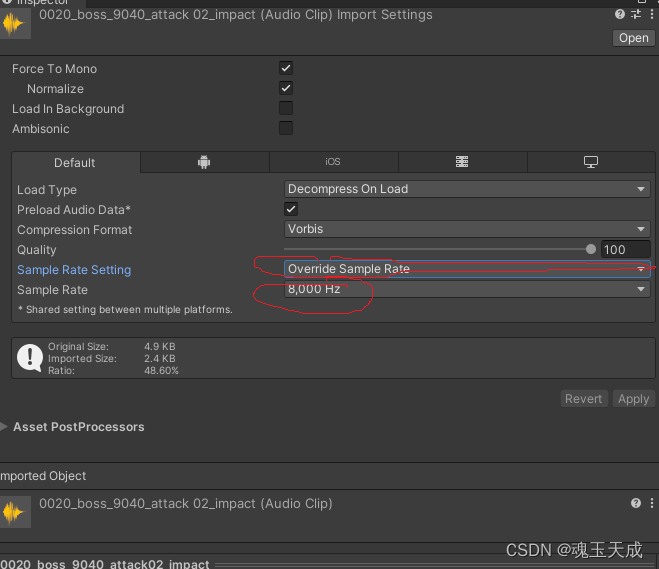
第一章:unity性能优化之内存优化
目录 前言 unity性能优化之内存的优化 一、unity Analysis工具的使用。 二、内存优化方法 1、设置和压缩图片 2、图片格式 3、动画文件 4、模型 5、RenderTexture(RT) 6、分辨率 7、资源的重复利用 8、shader优化 9、对bundle进行良好的管…...
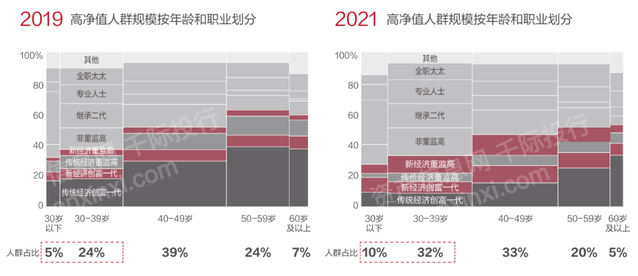
2023年家族办公室研究报告
第一章 概况 家族办公室最早起源于古罗马时期的大“Domus”(家族主管)以及中世纪时期的大“Domo”(总管家)。现代意义上的家族办公室出现于19世纪中叶,一些抓住产业革命机会的大亨将金融专家、法律专家和财务专家集合…...

Typescript快速入门
Typescript快速入门第一章 快速入门0、TypeScript简介1、TypeScript 开发环境搭建2、基本类型3、编译选项4、webpack5、Babel第二章:面向对象0、面向对象简介1、类(class)2、面向对象的特点3、接口(Interface)4、泛型&…...

如何激励你的内容团队产出更好的创意
对于一个品牌而言,如何创造吸引受众并对受众有价值内容是十分关键的。随着市场数字化的推进,优质的创意和内容输出对一个品牌在市场中有着深远的影响。对于很多内容策划和创作者来说,不断地产出高质量有创意的内容是一件非常有挑战性的事情。…...
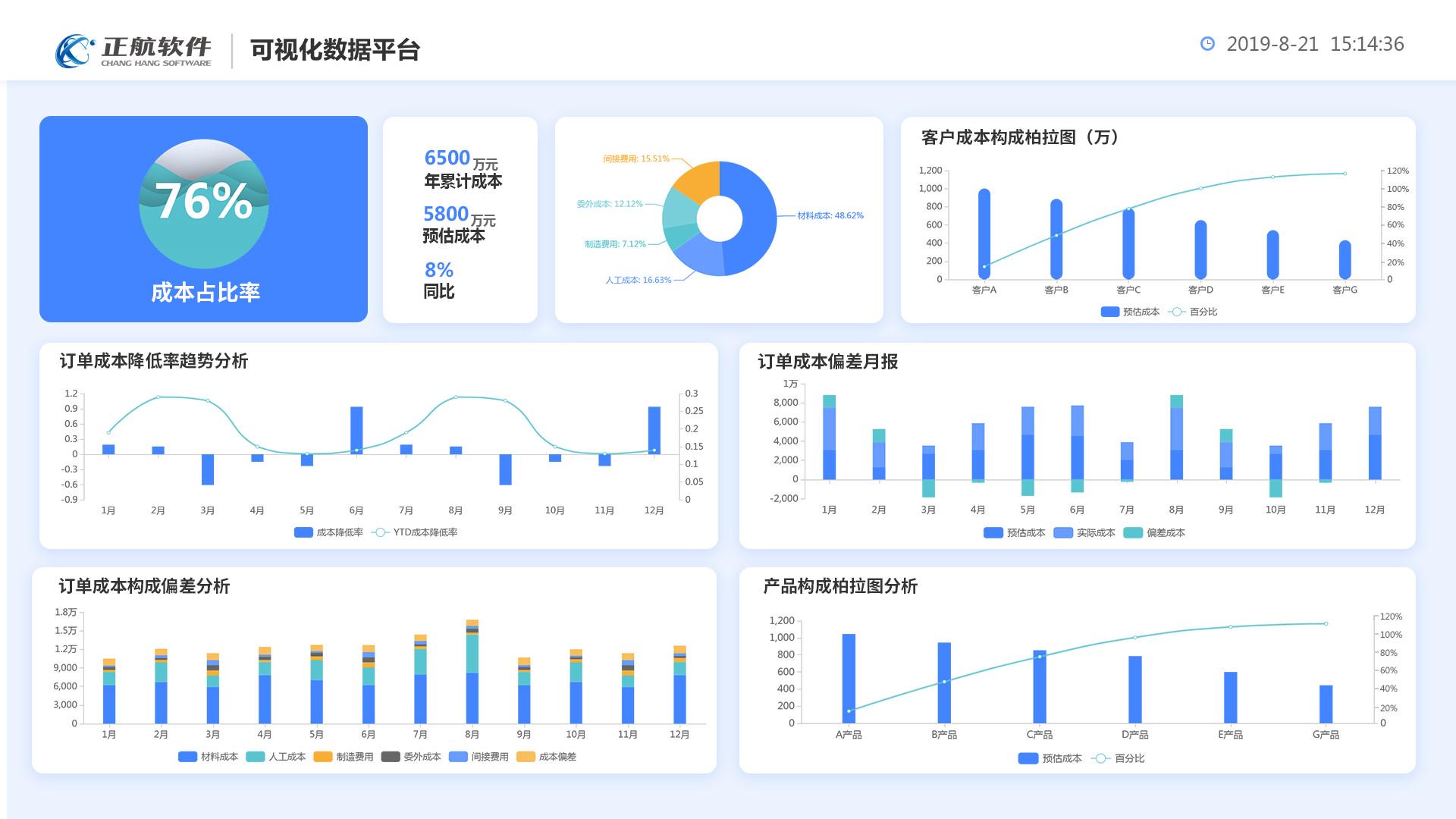
机械设备管理软件如何选择?机械设备管理软件哪家好?
随着信息化技术的进步与智能制造的发展趋势,很多机械设备制造企业也在一直探寻适合自己的数字化管理转型之路,而企业上ERP管理软件又是实现数字化管理的前提,机械设备管理软件对于企业来说就是关键一环。机械设备管理软件如何选择?…...
深入浅出带你学习shiro-550漏洞
//发点去年存货 前言 apache shiro是一个java安全框架,作用是提供身份验证,Apache Shiro框架提供了一个Rememberme的功能,存储在cookie里面的Key里面,攻击者可以使用Shiro的默认密钥构造恶意序列化对象进行编码来伪造用户的 Cookie…...

项目(今日指数之环境搭建)
一 项目架构1.1 今日指数技术选型【1】前端技术【2】后端技术栈【3】整体概览1.2 核心业务介绍【1】业务结构预览【2】业务结构预览1.定时任务调度服务XXL-JOB通过RestTemplate多线程动态拉去股票接口数据,刷入数据库; 2.国内指数服务 3.板块指数服务 4.…...

PCL 基于投影点密度的建筑物立面提取
目录 一、算法原理1、投影密度理论及方法2、参考文献二、代码实现三、结果展示一、算法原理 1、投影密度理论及方法 将3维坐标点直接垂直投影到水平面上或者将 Z Z Z 值取任意常数,统计和计算水平面任意位置处所含投影点的个数记为...

DDD 参考工程架构
1 背景 不同团队落地DDD所采取的应用架构风格可能不同,并没有统一的、标准的DDD工程架构。有些团队可能遵循经典的DDD四层架构,或改进的DDD四层架构,有些团队可能综合考虑分层架构、整洁架构、六边形架构等多种架构风格,有些在实…...

重建,是2023年的关键词
作者:俞敏洪 来源:老俞闲话(ID:laoyuxianhua) 01 重建,是2023年的关键词 1.重建,是2023年的关键词 2023年,以一种奇特的方式来临。 之所以说奇特,是因为我们谁都没有…...

动手写操作系统-00-环境搭建以及资料收集
文章目录 动手写操作系统内核目标编本教程适合什么样的人?一些简单的要求操作系统的功能环境搭建参考文档:动手写操作系统内核 一直以来想学习linux操作系统,读了很多关于操作系统的书籍,也想自己动手写个OS 目标编 编写一个操作系统内核;能正常的运行自己编写的OS本教程适合…...
【scipy.sparse包】Python稀疏矩阵详解
【scipy.sparse包】Python稀疏矩阵 文章目录【scipy.sparse包】Python稀疏矩阵1. 前言2. 导入包3. 稀疏矩阵总览4. 稀疏矩阵详细介绍4.1 coo_matrix4.2 dok_matrix4.3 lil_matrix4.4 dia_matrix4.5 csc_matrix & csr_matrix4.6 bsr_matrix5. 稀疏矩阵的存取5.1 用save_npz保…...

从写下第1个脚本到年薪30W,我的自动化测试心路历程
我希望我的故事能够激励现在的软件测试人,尤其是还坚持在做“点点点”的测试人。 你可能会有疑问:“我也能做到这一点的可能性有多大?”因此,我会尽量把自己做决定和思考的过程讲得更具体一些,并尽量体现更多细节。 …...
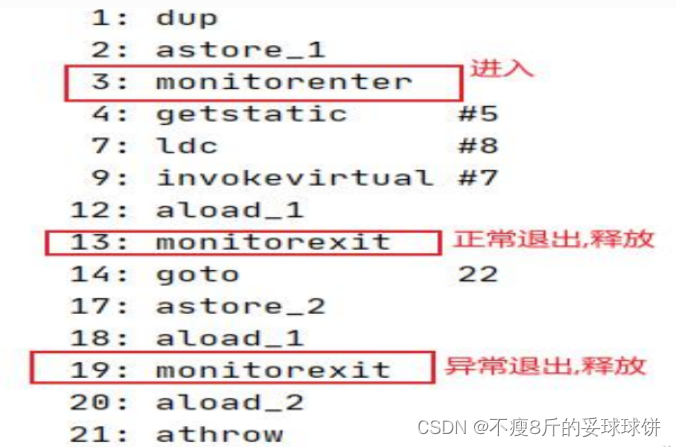
JAVA八股、JAVA面经
还有三天面一个JAVA软件开发岗,之前完全没学过JAVA,整理一些面经...... 大佬整理的:Java面试必备八股文_-半度的博客-CSDN博客 另JAVA学习资料:Java | CS-Notes Java 基础Java 容器Java 并发Java 虚拟机Java IO目录 int和Inte…...
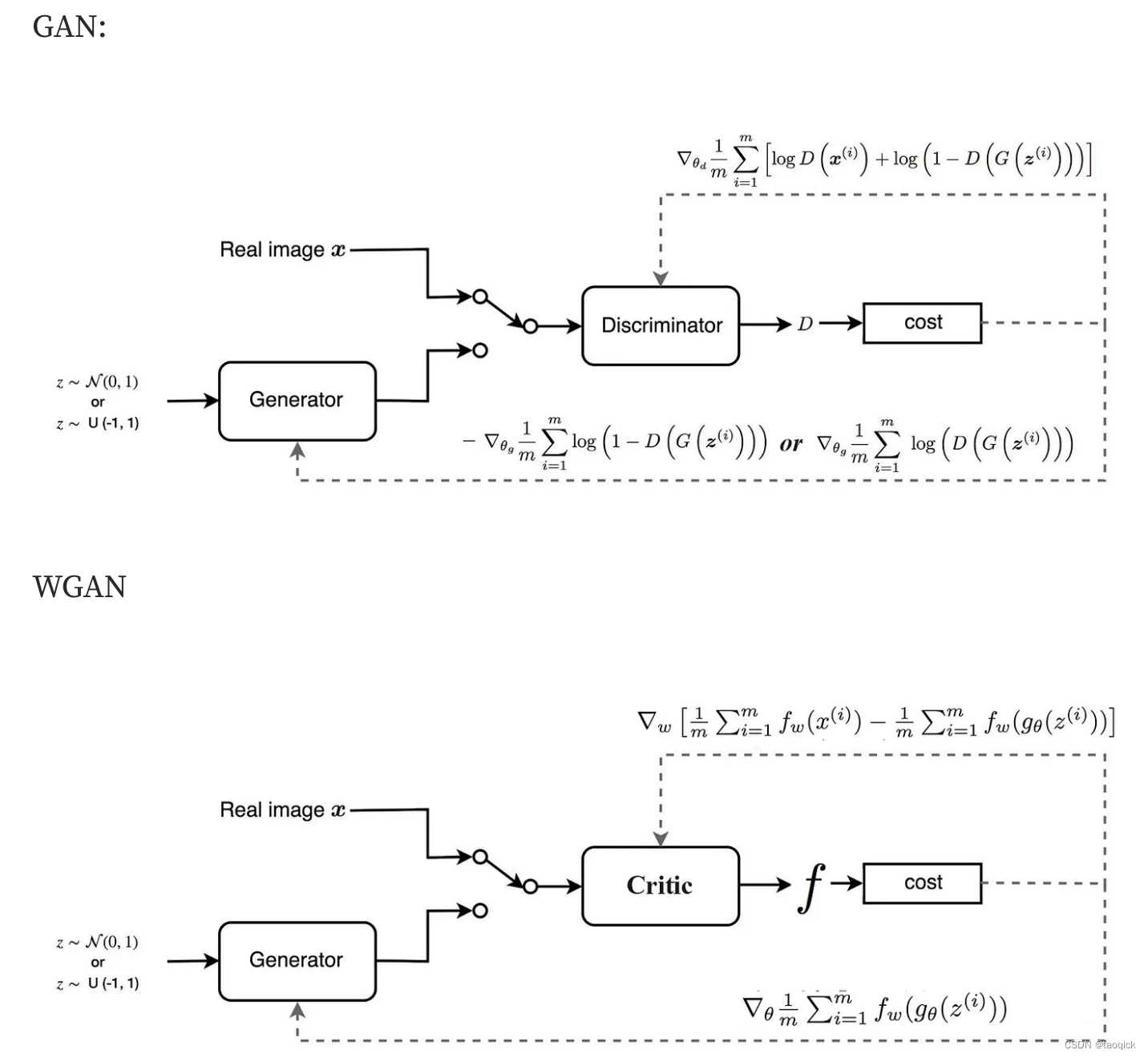
GAN系列基础知识
原始值函数 原始GAN的值函数是 minGmaxDV(D,G)Ex∼pdata(x)[logD(x)]Ez∼pz(z)[log(1−D(G(z)))]min_Gmax_DV(D,G) E_{x \sim p_{data}(x)}[logD(x)]E_{z \sim p_{z}(z)} [log(1-D(G(z)))]minGmaxDV(D,G)Ex∼pdata(x)[logD(x)]Ez∼pz(z)[log(1−D(G(z)))] 其中Ex…...
Linux/CenterOS 7.9配置汉化gitlab服务器
1.安装gitlab的依赖项 yum install -y curl openssh-server openssh-clients postfix cronie policycoreutils-python2.启动postfix,并设置为开机启动 systemctl start postfixsystemctl enable postfix3.防火墙和selinux的设置 setenforce 0systemctl stop fire…...

山洪灾害监测预警平台 山洪灾害监测预警系统解决方案 以人为本 科学防御
平升电子山洪灾害监测预警平台 山洪灾害监测预警系统解决方案,集信息采集、传输、分析和预警等功能于一体,实现预警信息及时、准确地上传下达,提升监测预警能力,使可能受灾区域能够及时采取措施,最大程度减少人员伤亡和…...

The Number Of ThreadPoolExecutor
序言整理下Java 线程池中线程数量如何设置的依据巨人肩膀:https://blog.csdn.net/weilaizhixing007/article/details/125955693https://blog.csdn.net/yuyan_jia/article/details/120298564#:~:text%E4%B8%80%E4%B8%AA%E7%BA%BF%E7%A8%8B%E6%B1%A0%E5%A4%84%E7%90%86%E8%AE%A1,…...

Linux(Linux各目录结构详解)
我们知道Linux系统是一个文件系统,它的文件系统就类似windows系统下的磁盘文件系统。 我们连接上一台linux系统的服务器。 输入命令 : ls / 我们可以看到 linux系统的根目录下有这些目录 bin boot data dev etc hbr home lib lib64 lostfoun…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
