买卖股票的最佳时机 IV - 困难
*************
C++
topic:188. 买卖股票的最佳时机 IV - 力扣(LeetCode)
*************
Stock angin:
 |
Still stocks. Intuitively, it feels hard.
For once:
class Solution {
public:int maxProfit(vector<int>& prices) {int minPrice = prices[0]; // 迄今为止遇到的最低价格int maxPro = 0; // 最大利润for (int i = 1; i < prices.size(); ++i) {// 如果当前价格比迄今为止的最低价格还低,更新最低价格if (prices[i] < minPrice) {minPrice = prices[i];} else {// 如果当前价格比最低价格高,计算利润,并更新最大利润maxPro = max(maxPro, prices[i] - minPrice);}}return maxPro;}
};For twice.
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size(); // get the lengthint firstBuy = - prices[0];int firstSale = 0;int secondBuy = - prices[0];int secondSale = 0;// do sth. herefor (int i = 1; i < n; i++){firstBuy = max(firstBuy, - prices[i]);firstSale = max(firstSale, prices[i] + firstBuy);// the second salesecondBuy = max(secondBuy, firstSale - prices[i]);secondSale = max(secondSale, prices[i] + secondBuy);}return secondSale;}
};For three times:
class Solution {
public:int maxProfit(vector<int>& prices) {if (prices.empty()) return 0;int n = prices.size();// 初始化状态变量int firstBuy = -prices[0]; // 第一次买入的最大利润int firstSell = 0; // 第一次卖出的最大利润int secondBuy = -prices[0]; // 第二次买入的最大利润int secondSell = 0; // 第二次卖出的最大利润int thirdBuy = -prices[0]; // 第三次买入的最大利润int thirdSell = 0; // 第三次卖出的最大利润for (int i = 1; i < n; ++i) {// 更新第一次买入的最大利润firstBuy = max(firstBuy, -prices[i]);// 更新第一次卖出的最大利润firstSell = max(firstSell, firstBuy + prices[i]);// 更新第二次买入的最大利润secondBuy = max(secondBuy, firstSell - prices[i]);// 更新第二次卖出的最大利润secondSell = max(secondSell, secondBuy + prices[i]);// 更新第三次买入的最大利润thirdBuy = max(thirdBuy, secondSell - prices[i]);// 更新第三次卖出的最大利润thirdSell = max(thirdSell, thirdBuy + prices[i]);}return thirdSell;}
};seems to have some idea.
I always think about one thing, if I had a mirror space, I could spare a whole life to learn how to code. After that, I enter another space to learn how to design. And go on studying playing balls and so on. However, I have only one time in this world and what I want to learn is too much with lazy mind. Rue always happen. I do some videos to record my travel and rember peoples whit me. Attracting fans sounds good but self happy means everythin. And guess what, I'll go on. Spare time from tiktok to code or work need some courage, and now I have some. All day's work just prove the plan not work, that's works do.

Chris Gardner, a stock trader, played in stocks. In the persuit of happyness, to be honest, I like this moment. Say yes to himself, in variable lives.
back to the topic, idea is find the fimilar things.
class Solution {
public:int maxProfit(vector<int>& prices) {if (prices.empty()) return 0;int n = prices.size();// 初始化状态变量int firstBuy = -prices[0]; // 第一次买入的最大利润int firstSell = 0; // 第一次卖出的最大利润int secondBuy = -prices[0]; // 第二次买入的最大利润int secondSell = 0; // 第二次卖出的最大利润int thirdBuy = -prices[0]; // 第三次买入的最大利润int thirdSell = 0; // 第三次卖出的最大利润int No.Buy = - prices[0];int No.Sale = 0;return thirdSell;}
};the loop could do the same:
class Solution {
public:int maxProfit(vector<int>& prices) {if (prices.empty()) return 0;int n = prices.size();// 初始化状态变量int firstBuy = -prices[0]; // 第一次买入的最大利润int firstSell = 0; // 第一次卖出的最大利润int secondBuy = -prices[0]; // 第二次买入的最大利润int secondSell = 0; // 第二次卖出的最大利润int thirdBuy = -prices[0]; // 第三次买入的最大利润int thirdSell = 0; // 第三次卖出的最大利润int No.Buy = - prices[0];int No.Sale = 0;for (int i = 1; i < n; ++i) {// 更新第一次买入的最大利润firstBuy = max(firstBuy, -prices[i]);// 更新第一次卖出的最大利润firstSell = max(firstSell, firstBuy + prices[i]);// 更新第二次买入的最大利润secondBuy = max(secondBuy, firstSell - prices[i]);// 更新第二次卖出的最大利润secondSell = max(secondSell, secondBuy + prices[i]);// 更新第三次买入的最大利润thirdBuy = max(thirdBuy, secondSell - prices[i]);// 更新第三次卖出的最大利润thirdSell = max(thirdSell, thirdBuy + prices[i]);No.Buy = max(No.Buy, No.-1Buy - prices[I]);
No.Sale = max(No.Sale, No.Sale + prices[I]);}return No.Sell;}
};Even people who doesnot know the code knows that the code doesnot runs, need some magic.
Now have two variables, i day and k times.
Define dp[i][j], the maximum profit in i days and trade j times. Then the most signifiicant eauation can be writed as
dp[i][j][sale] = max(dp[i-1][j][0], dp[i-1][j][1] + prices[i])dp[i][j][buy] = max(dp[i-1][j][1], dp[i-1][j-1][0] - prices[i])This method can easilly understood while the array comes to three-dimentional which is really hard to caculated. I can solve two-dimentional array problems. However, the three is a little bit hard.
For each day, you have two options, have the stock or donot have the stock.
For have the stock, you may have it yesterday or buy it today. So the maximum profit is
buy[j] = max(buy[j], sell[j - 1] - prices[i]);For donot have the stock, you may sold it yesterday or sold it today, so the maximum profit is
sell[j] = max(sell[j], buy[j] + prices[i]);Maybe it works but I am not sure, take a example:
prices = {3, 2, 6, 5, 0, 3};
k = 2day 0, price is 3
- j=1:
- buy[1] = max(buy[1], sell[0]-3) = max(INT_MIN, 0-3) = -3
- sell[1] = max(sell[1], buy[1]+3) = max(0, -3+3) = 0
- j=2:
- buy[2] = max(buy[2], sell[1]-3) = max(INT_MIN, 0-3) = -3
- sell[2] = max(sell[2], buy[2]+3) = max(0, -3+3) = 0
day 1,price = 2
- j=1:
- buy[1] = max(-3, sell[0]-2) = max(-3, 0-2) = -2
- sell[1] = max(0, -2+2) = 0
- j=2:
- buy[2] = max(-3, sell[1]-2) = max(-3, 0-2) = -2
- sell[2] = max(0, -2+2) = 0
day 2,price = 6:
- j=1:
- buy[1] = max(-2, 0-6) = -2
- sell[1] = max(0, -2+6) = 4
- j=2:
- buy[2] = max(-2, 4-6) = -2
- sell[2] = max(0, -2+6) = 4
day 3,price = 5:
- j=1:
- buy[1] = max(-2, 0-5) = -2
- sell[1] = max(4, -2+5) = 4
- j=2:
- buy[2] = max(-2, 4-5) = -2
- sell[2] = max(4, -2+5) = 4
day 4,price = 0:
- j=1:
- buy[1] = max(-2, 0-0) = 0
- sell[1] = max(4, 0+0) = 4
- j=2:
- buy[2] = max(-2, 4-0) = 4
- sell[2] = max(4, 4+0) = 4
day 5,price = 3:
- j=1:
- buy[1] = max(0, 0-3) = 0
- sell[1] = max(4, 0+3) = 4
- j=2:
- buy[2] = max(4, 4-3) = 4
- sell[2] = max(4, 4+3) = 7
OK, it works.
class Solution {
public:int maxProfit(int k, vector<int>& prices) {int n = prices.size();vector<int> buy(k + 1, INT_MIN), sell(k + 1, 0);for (int i = 0; i < n; i++) {for (int j = 1; j <= k; j++) {// 更新买入状态,即在第i天买入第j次的最大利润buy[j] = max(buy[j], sell[j - 1] - prices[i]);// 更新卖出状态,即在第i天卖出第j次的最大利润sell[j] = max(sell[j], buy[j] + prices[i]);}}// 最后返回卖出状态的最大值,即进行k次交易的最大利润return sell[k];}
};This week having some works to do. To be honest, this tipic is a little bit hard which takes me few days to work it.
Anyway, happy weekend.
相关文章:

买卖股票的最佳时机 IV - 困难
************* C topic:188. 买卖股票的最佳时机 IV - 力扣(LeetCode) ************* Stock angin: Still stocks. Intuitively, it feels hard. For once: class Solution { public:int maxProfit(vector<int>& prices) {in…...

linux源码编译php提示:No package ‘oniguruma‘ found
编译遇到缺少Oniguruma开发包,处理办法1 安装epel仓库、安装 Oniguruma 开发包 [rootiZwz98gb9fzslgpnomg3ceZ php-8.1.29]# yum install epel-release [rootiZwz98gb9fzslgpnomg3ceZ php-8.1.29]# yum install oniguruma oniguruma-devel 方法2:去On…...
2024技能大赛Vue流程复现
1. 关于版本的控制 vue/cli 5.0.8vscode 最新下载版本 2. 创建vuecli项目 若没有安装vuecli则可以先安装 npm install -g vue/cli # 默认下载最新版本。vue --version vue -V # 查看版本,两个选一 使用vuecli来创建一个新的vue项目,vs code打开…...
MATLAB截取图像的一部分并保存导出,在itksnap中3D展示
**问题描述:**输入nifti图像,截取图像的一部分并输出,比如截取图像的101010这一块,并导出为nii文件 inputFile D:\aa\dcm\input.nii; % 输入文件路径subsetSize [10 10 10]; % 截取的图像块大小 subsetStart [1 1 1]; % 截取的…...
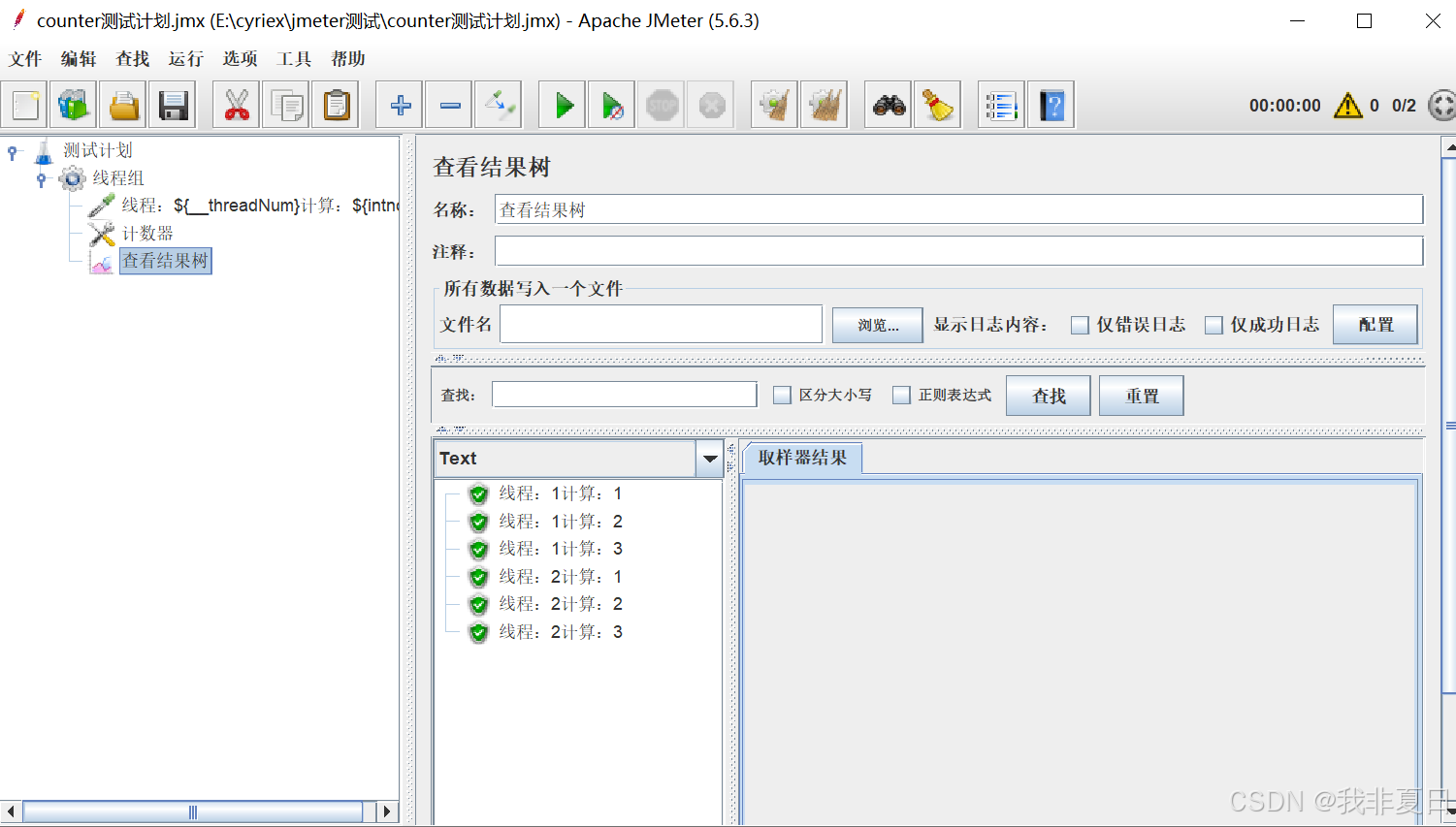
JMeter配置原件-计数器
一、面临的问题: 由于本人的【函数助手对话框】中counter计数器每次加2,且只显示偶数(如下图所示),因此借助【配置原件-计数器】来实现计数功能。 如果有大佬知道解决方式,麻烦评论区解答一下,谢谢。 二、配置原件-c…...

go面试问题
1 Go的内存逃逸如何分析 go build -gcflags-m main_pointer.go 2 http状态码 300 请求的资源可包括多个位置,相应可返回一个资源特征与地址的列表用于用户终端(例如:浏览器)选择 301 永久移动。请求的资源已被永久的移动到新U…...

springboot 配置Kafka 关闭自启动连接
这里写自定义目录标题 springboot 配置Kafka 关闭自启动连接方法一:使用 ConditionalOnProperty方法二:手动管理Kafka监听器容器方法三:使用 autoStartupfalse结语 springboot 配置Kafka 关闭自启动连接 在Spring Boot应用程序中,…...
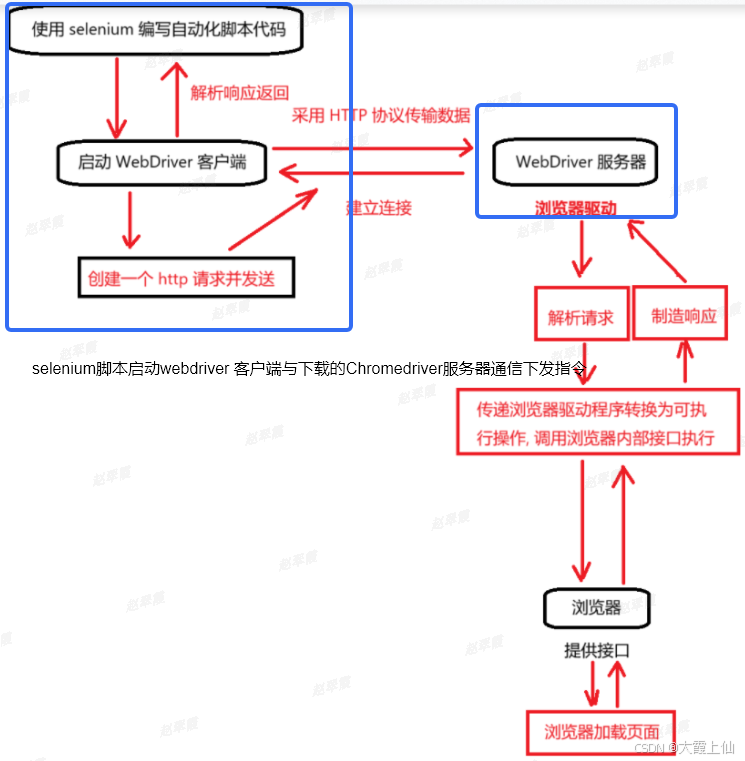
selenium工作原理
原文链接:https://blog.csdn.net/weixin_67603503/article/details/143226557 启动浏览器和绑定端口 当你创建一个 WebDriver 实例(如 webdriver.Chrome())时,Selenium 会启动一个新的浏览器实例,并为其分配一个特定的…...
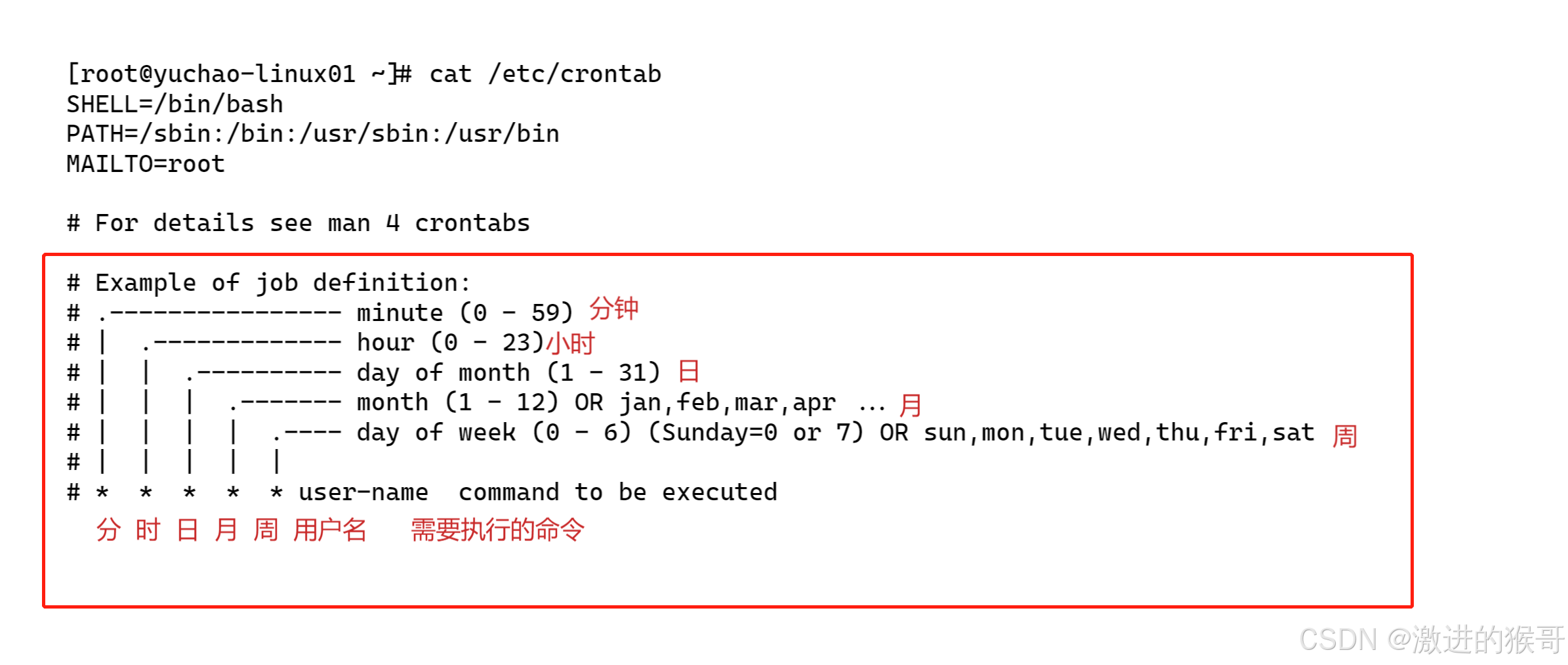
day14-16系统服务管理和ntp和防火墙
一、自有服务概述 服务是一些特定的进程,自有服务就是系统开机后就自动运行的一些进程,一旦客户发出请求,这些进程就自动为他们提供服务,windows系统中,把这些自动运行的进程,称为"服务" window…...

Hadoop、Hbase使用Snappy压缩
1. 前期准备 系统环境:centos7.9 配置信息:8C8G100G hadoop和hbase为单节点部署模式 jdk版本jdk1.8.0_361 1.1. 修改系统时间 timedatectl set-timezone <TimeZone> 1.2. 修改主机名以及主机名和IP的映射 vim /etc/hosts #将自己的主机名以及…...

【python】OpenCV—Image Moments
文章目录 1、功能描述2、图像矩3、代码实现4、效果展示5、完整代码6、涉及到的库函数cv2.moments 7、参考 1、功能描述 计算图像的矩,以质心为例 2、图像矩 什么叫图像的矩,在数字图像处理中有什么作用? - 谢博琛的回答 - 知乎 https://ww…...
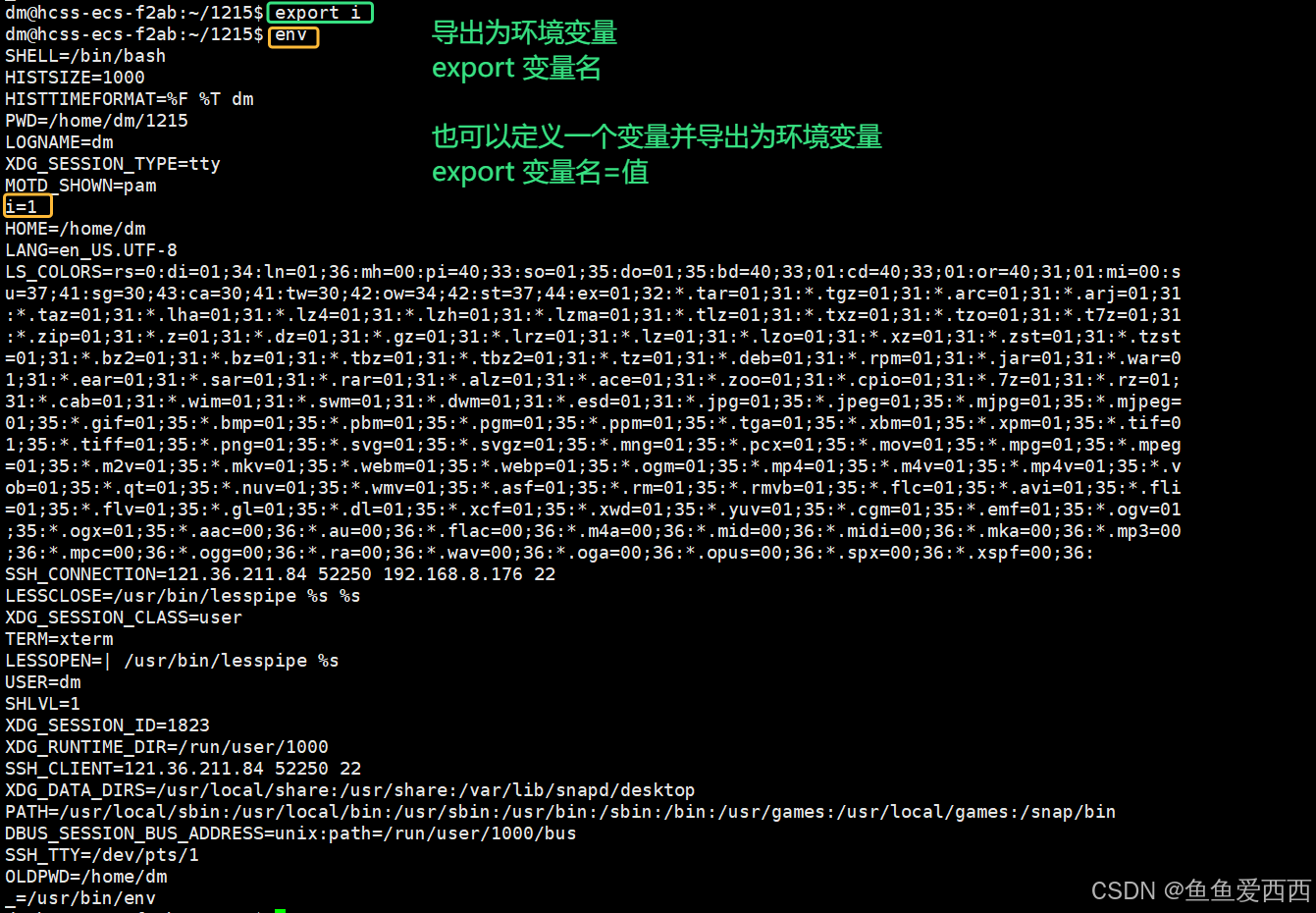
环境变量的知识
目录 1. 环境变量的概念 2. 命令行参数 2.1 2.2 创建 code.c 文件 2.3 对比 ./code 执行和直接 code 执行 2.4 怎么可以不带 ./ 2.4.1 把我们的二进制文件拷贝到 usr/bin 路径下,也不用带 ./ 了 2.4.2 把我们自己的路径添加到环境变量里 3. 认识PATH 3.…...
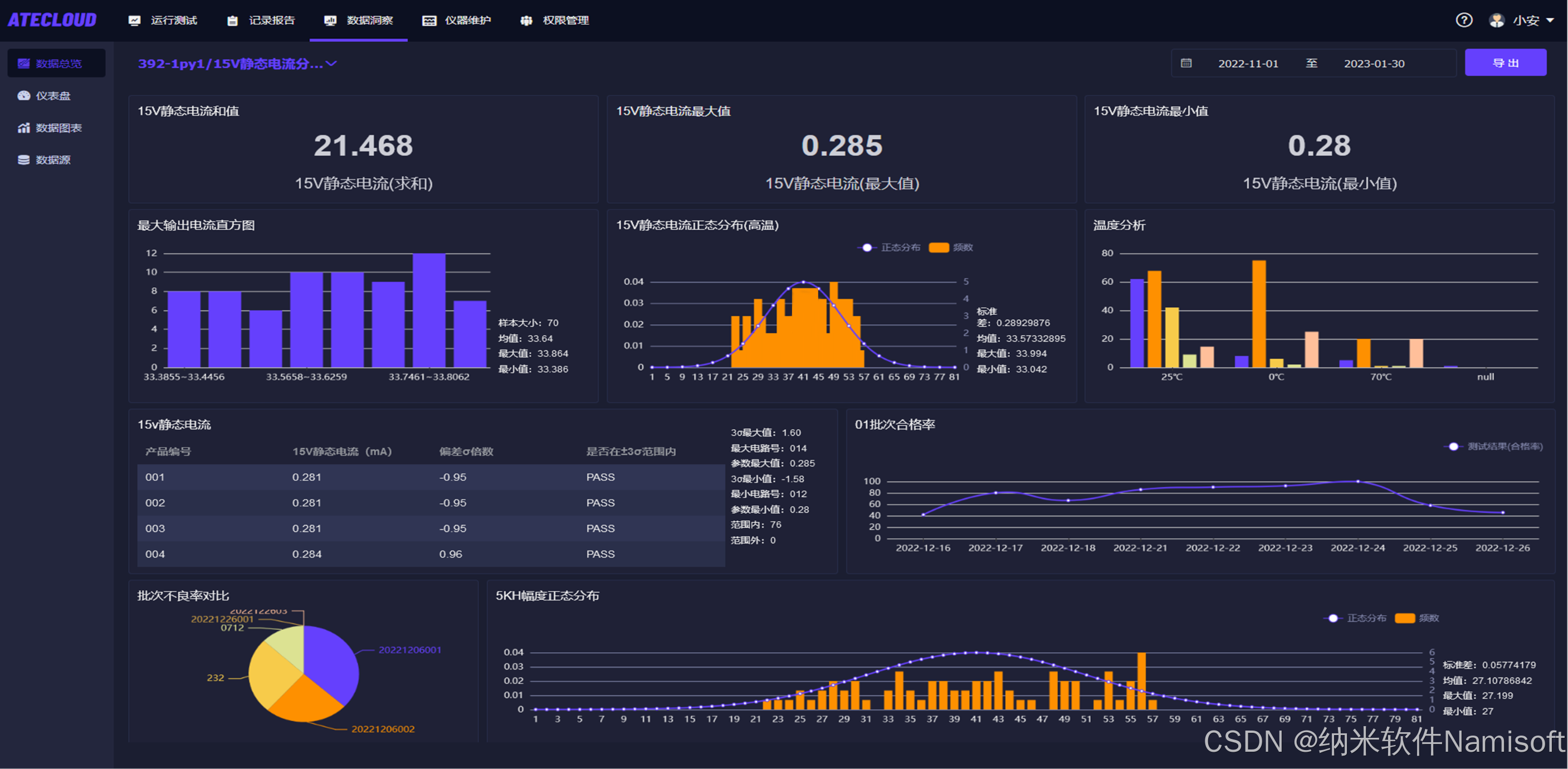
ATECLOUD测试平台有哪些功能?
测试方案搭建 可视化拖拽编程:采用零代码的图文拖拽形式,用户通过鼠标拖拽节点和连线,即可可视化地构建测试模型,无需懂得代码开发,15 分钟左右就能快速搭建项目,大大降低了上手门槛。 子项目多层嵌套&am…...
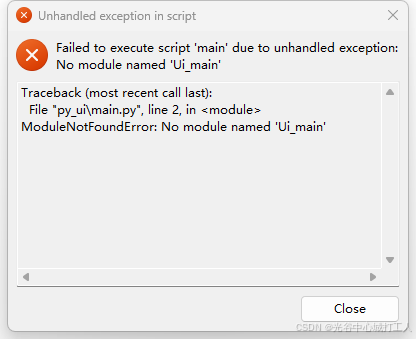
使用pyinstaller打包pyqt的程序,运行后提示ModuleNotFoundError: No module named ‘Ui_main‘
环境:windowpython3.9pyqt6 使用pyqt UI编辑器生成了main.ui ,main.ui编译成了Ui_main.py main.py 使用当前目录下的Ui_main.py。 打包过程没报错,运行报错。 错误如下: 解决方法:pyinstaller -Fw main.py --paths. 使…...

搭建分布式Spark集群
title: 搭建分布式Spark集群 date: 2024-11-29 12:00:00 categories: - 服务器 tags: - Spark - 大数据搭建分布式Spark集群 本次实验环境:Centos 7-2009、Hadoop-3.1.4、JDK 8、Zookeeper-3.6.3、scala-2.11.5、Spark-3.2.1 功能规划 MasterSlave1Slave2主节点…...

Django基础 - 01入门简介
一、 基本概念 1.1 Django说明 Django发布于2005年, 网络框架, 用Python编写的开源的Web应用框架。采用了MVC框架模式,也称为MTV模式。官网: https://www.djangoproject.com1.2 MVC框架 Model: 封装和数据库相关…...

简单的bytebuddy学习笔记
简单的bytebuddy学习笔记 此笔记对应b站bytebuddy学习视频进行整理,此为视频地址,此处为具体的练习代码地址 一、简介 ByteBuddy是基于ASM (ow2.io)实现的字节码操作类库。比起ASM,ByteBuddy的API更加简单易用。开发者无需了解class file …...

【服务端】Redis 内存超限问题的深入探讨
在 Java 后端开发中,Redis 内存超限是一个常见的问题,可能由多种原因引起。理解这些原因以及如何处理已经超出限制的数据对于保持系统的稳定性和性能至关重要。 一、Redis 内存超限的原因分析 Redis 是一个高性能的内存键值对存储系统,它在…...
)
Springboot logback 日志打印配置文件,每个日志文件100M,之后滚动到下一个日志文件,日志保留30天(包含traceid)
全部配置 logback.xml <?xml version"1.0" encoding"UTF-8"?> <configuration debug"false"><property name"LOG_HOME" value"log"/><property name"LOG_NAME" value"admin"/&g…...

《计算机组成及汇编语言原理》阅读笔记:p1-p8
《计算机组成及汇编语言原理》学习第 1 天,p1-p8 总结,总计 8 页。 一、技术总结 1.Intel 8088 microprocessor(微处理器), 1979-1988。 2.MS-DOS Microsoft Disk Operating System的缩写,是一个操作系统(operating system)。…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
