机器学习之KNN算法
K-Nearest Neighbors (KNN) 是一种常见的机器学习算法,广泛应用于分类和回归问题。KNN是一种基于实例的学习方法,它利用训练数据集的实例来进行分类或回归预测。在KNN中,预测的结果依赖于距离度量函数计算出的最近邻实例的标签或值。下面我们将详细探讨KNN的工作原理,并通过代码和示例进一步说明其应用。
KNN算法的原理
- 训练阶段:
- KNN 是一种 懒惰学习算法,即在训练阶段,算法并不建立显式的模型,只是简单地存储所有的训练数据。它不会对数据进行任何处理,直到遇到测试数据时才会进行计算。
- 预测阶段:
- 对于每个待分类(或待回归)的样本,KNN 计算该样本与训练集中所有样本的距离。常用的距离度量包括 欧氏距离(Euclidean Distance)、曼哈顿距离(Manhattan Distance)、切比雪夫距离(Chebyshev Distance) 等。
- 然后,选择 K 个最近的邻居,根据这些邻居的信息来做出预测。
- 分类任务:通过多数投票原则,选择最常见的类别作为预测结果。
- 回归任务:通过取 K 个邻居的平均值来预测目标值。
KNN的工作流程
- 选择K值:选择一个适当的 K 值,即选择最近邻的数量。K的值过小可能会导致过拟合,过大可能会导致欠拟合。
- 计算距离:选择适当的距离度量方法,最常用的是 欧氏距离。
- 预测:
- 分类任务:通过投票选出 K 个邻居中出现最多的类别作为预测结果。
- 回归任务:计算 K 个邻居的均值作为预测结果。
KNN的优势与劣势
优势
- 简单易懂:KNN是一种直观且简单的算法,容易实现。
- 不需要训练阶段:KNN没有显式的训练过程,直接将数据存储并用于预测。
- 能够处理多类别分类问题:KNN算法可以同时处理多个类别的数据。
- 自适应性强:由于KNN是基于实例的,不需要构建复杂的模型,可以灵活地适应不同类型的学习任务。
劣势
- 计算开销大:KNN算法在测试阶段需要计算每个测试样本与所有训练样本的距离,因此计算量较大,尤其在数据集较大的情况下。
- 内存开销大:由于KNN需要存储所有训练数据,内存消耗较高。
- 对异常值敏感:KNN对数据中的异常值较为敏感,异常值可能会严重影响模型的性能。
- 高维数据问题:KNN在高维空间中表现较差,这被称为“维度灾难”(Curse of Dimensionality)。随着维度的增加,样本之间的距离趋于相等,使得KNN的效果下降。
如何选择K值
选择K值的大小对于模型的表现至关重要。一般来说,较小的K值可能导致模型对训练数据中的噪声过于敏感,而较大的K值则可能导致模型的预测结果过于平滑,忽略了局部数据的特征。通常,可以通过交叉验证来选择最优的K值。
距离度量方法
在KNN中,选择合适的距离度量非常重要。以下是几种常见的距离度量方法:
-
欧氏距离(Euclidean Distance): 欧氏距离是最常见的距离度量方法,适用于连续变量。

其中,x和 y 是两个向量,xi 和 yi是它们的第 i 个维度。
-
曼哈顿距离(Manhattan Distance): 曼哈顿距离计算的是两个点在所有维度上差值的绝对值之和。

-
切比雪夫距离(Chebyshev Distance): 切比雪夫距离计算的是两个点在各维度上差值的最大值。

KNN算法的代码实现
下面是一个简单的KNN算法实现,使用了 欧氏距离 作为度量标准。
示例:使用Python实现KNN算法
import numpy as np
from collections import Counter# 计算欧氏距离
def euclidean_distance(x1, x2):return np.sqrt(np.sum((x1 - x2)**2))# KNN算法实现
class KNN:def __init__(self, k=3):self.k = k # 设置 K 值def fit(self, X_train, y_train):self.X_train = X_trainself.y_train = y_traindef predict(self, X_test):predictions = [self._predict(x) for x in X_test]return np.array(predictions)def _predict(self, x):# 计算测试点与训练数据的距离distances = [euclidean_distance(x, x_train) for x_train in self.X_train]# 按照距离排序并选择最近的K个点k_indices = np.argsort(distances)[:self.k]k_nearest_labels = [self.y_train[i] for i in k_indices]# 返回出现次数最多的标签most_common = Counter(k_nearest_labels).most_common(1)return most_common[0][0]# 示例数据
X_train = np.array([[1, 2], [2, 3], [3, 4], [6, 7], [7, 8], [8, 9]]) # 训练数据
y_train = np.array([0, 0, 0, 1, 1, 1]) # 标签X_test = np.array([[2, 2], [7, 7]]) # 测试数据# 创建并训练KNN模型
knn = KNN(k=3)
knn.fit(X_train, y_train)# 预测
predictions = knn.predict(X_test)
print(f"Predictions: {predictions}")
代码解释:
- 欧氏距离计算:
euclidean_distance()计算两个点之间的欧氏距离。 - KNN类:
fit():用于存储训练数据。predict():对每个测试样本进行预测。_predict():对单个样本,根据最近的 K 个邻居进行预测。
- 示例数据:
X_train和y_train分别是训练数据和标签,X_test是需要预测的测试数据。
运行结果:
Predictions: [0 1]
KNN算法的应用场景
-
分类问题:KNN在文本分类、图像分类、医疗诊断等领域有广泛应用。例如,根据用户的历史行为预测用户是否会点击广告,或者根据病人的症状预测是否患有某种疾病。
-
回归问题:KNN也可用于回归问题,如房价预测、股票市场预测等。通过选择 K 个最相似的样本,计算这些样本的目标值的平均值来做出预测。
KNN的优缺点
优点:
- 简单易理解:KNN算法非常简单,易于理解和实现。
- 无需训练:KNN是懒惰学习算法,不需要显式的训练过程。
- 适应性强:KNN可以轻松地适应多类别和多维度的数据。
缺点:
- 计算复杂度高:在测试阶段,KNN需要计算每个测试样本与所有训练样本的距离,计算量较大,尤其是在大规模数据集上。
- 内存消耗大:KNN算法需要存储所有的训练数据,内存消耗较大。
- 对噪声敏感:KNN对于数据中的噪声较为敏感,特别是在高维数据中。
- 不适合高维数据:在高维空间中,距离度量变得不再有效,KNN的效果显著下降。
创建自己的 KNN 可视化图
你可以使用 matplotlib 和 sklearn 来生成一个简单的 KNN 可视化图。下面是一个 Python 代码示例:
import numpy as np
from sklearn.datasets import make_classification
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt# 生成数据集
X, y = make_classification(n_samples=100, n_features=5, n_informative=2, random_state=42)# 创建 KNN 分类器并进行训练
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X, y)# 创建一个用于预测的网格(要确保特征数与训练时一致)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))# 现在我们需要确保输入的数据有 5 个特征
# 创建一个数据集,注意这里我们需要保持与训练集相同的特征数量
grid_points = np.c_[xx.ravel(), yy.ravel(), np.zeros((xx.ravel().shape[0], 3))]# 使用 KNN 模型进行预测
Z = knn.predict(grid_points)# 绘制决策边界
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o', s=50)
plt.show()
生成图的过程是基于 KNN(K-Nearest Neighbors)分类器的决策边界可视化。

以下是整个图生成过程的详细解释:
1. 生成数据集
我们使用 make_classification 函数生成一个人工数据集,这个数据集有 100 个样本和 5 个特征,其中 2 个特征是有信息量的(即能帮助分类),其余的特征是冗余或无关的。数据集的目标是模拟实际分类任务中的数据。
X, y = make_classification(n_samples=100, n_features=5, n_informative=2, random_state=42)
X: 是特征矩阵,包含 100 个样本,每个样本有 5 个特征。y: 是每个样本对应的标签(分类结果)。
2. 训练 KNN 分类器
我们用生成的数据训练一个 KNN 分类器:
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X, y)
KNeighborsClassifier(n_neighbors=3):创建一个 KNN 分类器,使用 3 个邻居进行分类。knn.fit(X, y):使用X和y进行模型训练。
3. 创建网格用于预测
为了展示 KNN 分类器的决策边界,我们需要生成一个包含所有可能输入点的网格。网格点的数量决定了我们图像的分辨率,网格是通过对特征空间进行划分得到的。
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))
xx和yy是通过np.meshgrid生成的网格的坐标。np.arange(x_min, x_max, 0.1)会创建一个从x_min到x_max的数值序列,步长为0.1,同理np.arange(y_min, y_max, 0.1)会创建从y_min到y_max的数值序列。xx, yy:它们的形状分别是(height, width),代表平面坐标的网格。
4. 确保网格输入特征一致
由于我们训练模型时使用了 5 个特征,但网格生成时只有 2 个特征,因此我们需要填充额外的 3 个特征,以确保输入特征的维度和训练时一致。
grid_points = np.c_[xx.ravel(), yy.ravel(), np.zeros((xx.ravel().shape[0], 3))]
np.c_[]是一个方便的功能,用于将数组按列连接。xx.ravel()和yy.ravel()将网格坐标转换为一维数组,然后我们通过np.zeros向每个点添加额外的 3 个特征(这些特征是0,不会影响预测的结果)。
5. 进行预测
现在,网格上的每一个点都包含了 5 个特征,我们可以将这些点输入到训练好的 KNN 模型中,进行预测:
Z = knn.predict(grid_points)
grid_points是形状为(N, 5)的数组,N是网格点的总数(例如,3000 个点)。knn.predict(grid_points)将输出每个点的分类标签。
6. 绘制决策边界
接下来,我们可以绘制出 KNN 分类器的决策边界。这是通过对 xx 和 yy 进行 Z.reshape(xx.shape) 转换,将预测的分类结果与网格坐标对应起来,然后用 plt.contourf() 绘制填充的等高线来展示。
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8)
Z.reshape(xx.shape)将Z的形状调整为与xx相同的形状,确保与网格坐标对齐。plt.contourf()用于绘制决策边界的填充等高线图。alpha=0.8设置透明度,使得决策区域的颜色更加柔和。
7. 绘制数据点
最后,我们用 plt.scatter() 绘制数据点,显示训练数据的分布。X[:, 0] 和 X[:, 1] 分别是数据的前两个特征,用于二维图中显示:
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o', s=50)
X[:, 0]和X[:, 1]是数据的前两个特征(我们只用前两个特征来显示图)。c=y用于根据标签y给每个点上色。edgecolors='k'用于设置点的边缘颜色为黑色。
8. 显示图像
最终,使用 plt.show() 来显示绘制的图像:
plt.show()
总结:
- 决策边界:通过网格点进行预测,我们可以看到不同类别的决策边界。这些边界代表了分类器如何将输入空间划分为不同的类。
- 数据点分布:图中的散点表示了数据点的位置,颜色代表不同的类别。
- 分类器的影响:不同的 K 值和距离度量会影响决策边界的形状,从而影响分类的效果。
总结
KNN是一个简单但强大的机器学习算法,适用于分类和回归任务。通过选择合适的K值和距离度
量方式,可以获得很好的性能。然而,KNN的计算和内存开销较大,尤其是在数据集较大的时候,因此在实际应用中需要注意其优缺点,并根据具体问题进行调整和优化。
相关文章:

机器学习之KNN算法
K-Nearest Neighbors (KNN) 是一种常见的机器学习算法,广泛应用于分类和回归问题。KNN是一种基于实例的学习方法,它利用训练数据集的实例来进行分类或回归预测。在KNN中,预测的结果依赖于距离度量函数计算出的最近邻实例的标签或值。下面我们…...

《全排列问题》
题目描述 按照字典序输出自然数 11 到 nn 所有不重复的排列,即 nn 的全排列,要求所产生的任一数字序列中不允许出现重复的数字。 输入格式 一个整数 nn。 输出格式 由 1∼n1∼n 组成的所有不重复的数字序列,每行一个序列。 每个数字保留…...

pycharm 快捷键
PyCharm 是一款功能强大的集成开发环境(IDE),提供了丰富的快捷键来提高开发效率。以下是一些常用的 PyCharm 快捷键(基于 Windows/Linux 系统,Mac 系统可能略有不同): 通用快捷键 功能快捷键&a…...

若依微服务如何获取用户登录信息
文章目录 1、需求提出2、应用场景3、解决思路4、注意事项5、完整代码第一步:后端获取当前用户信息第二步:前端获取当前用户信息 5、运行结果6、总结 1、需求提出 在微服务架构中,获取当前用户的登录信息是开发常见的需求。无论是后端处理业务…...

RunCam WiFiLink连接手机图传测试
RunCam WiFiLink中文手册从这里下载 一、摄像头端 1.连接天线(易忘) 2.打开摄像头前面的盖子(易忘) 3.接上直流电源,红线为正,黑线为负 4.直流电源设置电压为14v,电流为3.15A, 通…...

TCP三次握手,四次挥手
三次握手 第一次握手:客户端向服务器发送一个 SYN 包,其中 SYN 标志位被设置为 1,表示客户端请求建立连接,并随机生成一个初始序列号 seqx 。此时客户端进入 SYN_SENT 状态,等待服务器的确认1.第二次握手:服…...

Mono里建立调试C#脚本运行环境
前面已经介绍了怎么样来执行一个嵌入式的脚本框架, 这个框架是mono编写的一个简单的例子。 如果不清楚,可以参考前文: https://blog.csdn.net/caimouse/article/details/144632391?spm=1001.2014.3001.5501 本文主要来介绍一下,我们的C#脚本是长得怎么样的,它大体如下…...

Linux dnf 包管理工具使用教程
简介 dnf 是基于 Red Hat Linux 发行版的下一代包管理工具,它代替 yum 提供更好的性能、更好的依赖处理和更好的模块化架构。 基础语法 dnf [options] [command] [package] 常用命令用法 更新元数据缓存 sudo dnf check-update# 检查已安装的包是否有可用的更…...

Java 创建线程的方式有哪几种
在 Java 中,创建线程的方式有四种,分别是:继承 Thread 类、实现 Runnable 接口、使用 Callable 和 Future、使用线程池。以下是详细的解释和通俗的举例: 1. 继承 Thread 类 通过继承 Thread 类并重写 run() 方法来创建线程。 步…...

计算机的错误计算(一百八十七)
摘要 用大模型计算 sin(123.456789). 其自变量为弧度。结果保留16位有效数字。第一个大模型是数学大模型。先是只分析,不计算;后经提醒,才给出结果,但是是错误结果。第二个大模型,直接给出了Python代码与结果…...
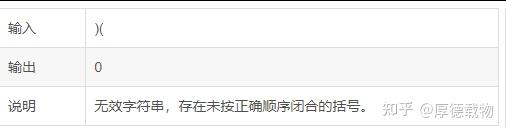
12. 最大括号深度
题目描述 现有一字符串仅由"(",")", "{","}", "[", "]"六种括号组成。若字符串满足以下条件之一, 则为无效字符串:任一类型的左右括号数量不相等 存在未按正确顺序(先左后右)闭合的括号输出…...

进程与线程以及如何查看
长期补充,建议关注收藏! 定义 特性进程线程定义程序执行的基本单位执行中的最小单位资源拥有独立的内存空间和资源共享进程的资源开销创建和销毁的开销较大创建和销毁的开销较小执行单位进程中可以有多个线程线程是执行单元,必须依赖于进程并…...
BlueLM:以2.6万亿token铸就7B参数超大规模语言模型
一、介绍 BlueLM 是由 vivo AI 全球研究院自主研发的大规模预训练语言模型,本次发布包含 7B 基础 (base) 模型和 7B 对话 (chat) 模型,同时我们开源了支持 32K 的长文本基础 (base) 模型和对话 (chat) 模型。 更大量的优质数据 :高质量语料…...

Webpack学习笔记(4)
1.缓存 可以通过命中缓存降低网络流量,是网站加站速度更快。 然而在部署新版本时,不更改资源的文件名,浏览器可能认为你没有更新,所以会使用缓存版本。 由于缓存存在,获取新的代码成为问题。 接下来将配置webpack使…...

28、论文阅读:基于像素分布重映射和多先验Retinex变分模型的水下图像增强
A Pixel Distribution Remapping and Multi-Prior Retinex Variational Model for Underwater Image Enhancement 摘要介绍相关工作基于模型的水下图像增强方法:无模型水下图像增强方法:基于深度学习的水下图像增强方法: 论文方法概述像素分布…...

5.interview-self-introduction
1.保证电话面试来的时候,可以接听,保持电话通常 interviews will be arranged recently.please keep your phone line open and make sure you can answer th call when the phone interview comes. speak loudly and slow down your speaking voice &a…...

高性能MySQL-查询性能优化
查询性能优化 1、为什么查询这么慢2、慢查询基础:优化数据访问2.1 是否向数据库请求了不需要的数据2.2 MySQL是否存在扫描额外的记录 3、重构查询方式3.1 一个复杂查询还是多个简单查询3.2 切分查询3.3 分解联接查询 4、查询执行的基础4.1 MySQL的客户端/服务器通信…...

如何有效修复ffmpeg.dll错误:一站式解决方案指南
当您遇到提示“ffmpeg.dll文件丢失”的错误时,这可能导致相关的应用程序无法启动或运行异常。本文将详细介绍如何有效地解决ffmpeg.dll文件丢失的问题,确保您的应用程序能够恢复正常运行。 ffmpeg.dll是什么?有哪些功能? ffmpeg.…...
8086汇编(16位汇编)学习笔记00.DEBUG命令使用解析及范例大全
8086汇编(16位汇编)学习笔记00.DEBUG命令使用解析及范例大全-C/C基础-断点社区-专业的老牌游戏安全技术交流社区 - BpSend.net[md]启动 Debug,它是可用于测试和调试 MS-DOS 可执行文件的程序。 Debug [[drive:][path] filename [parameters]] 参数 [drive:…...

查看mysql的冷数据配置比例
查看mysql的冷数据配置比例 -- 真正的LRU链表,会被拆分为两个部分,一部分是热数据,一部分是冷数据,这个冷热数据的比例是由innodb_old_blocks_pct参数控制的,它默认是37,也就是说冷数据占比37%。 show GLO…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
