C#(委托)
一、基本定义
在C#中,委托(Delegate)是一种引用类型,它用于封装一个方法(具有特定的参数列表和返回类型)。可以把委托想象成一个能存储方法的变量,这个变量能够像调用普通方法一样来调用它所存储的方法。
例如,有一个方法void PrintMessage(string message),可以定义一个委托来存储对这个方法的引用,之后通过委托调用PrintMessage方法。
二、作用类比
就好比在一个工具库中,委托是一种特殊的 “工具槽”。这个 “工具槽” 有特定的形状(对应委托的参数列表和返回类型要求),只有符合这个形状的工具(方法)才能放入。一旦放入了工具(方法),就可以通过这个“工具槽”(委托)来使用该工具(调用方法)。
三、语法结构
委托的定义语法是delegate returnType DelegateName(parameterList);。
其中returnType表示委托所引用方法的返回类型,DelegateName是委托的名称,parmeterList是委托所引用方法的参数列表。
例如,定义一个委托来引用一个返回int类型并且接收两个int参数的方法:delegate int MathDelegate(int num1,int num2);
四、实际用途
作为方法参数传递:这是委托很重要的一个用途。假设你有一个排序算法方法SortArray(int[] Array,Comparison<int> comparer),其中Comparison<int>是一个委托类型,它用于定义两个整数比较的规则。这样就可以将不同的比较方法作为参数传递给排序算法,实现不同方式的排序,比如按照升序或者降序排序。
事件处理:在图形用户界面(GUI)编程或者其他事件驱动的编程场景中,委托起着关键作用。例如,在Windows Forms或者WPF应用中,按钮的Click事件实际上是一个委托。当按钮被点击时,会调用这个委托所关联的方法,从而执行相应的操作,如弹出一个消息框或者执行一些数据更新操作。
C#练习22
相关文章:
)
C#(委托)
一、基本定义 在C#中,委托(Delegate)是一种引用类型,它用于封装一个方法(具有特定的参数列表和返回类型)。可以把委托想象成一个能存储方法的变量,这个变量能够像调用普通方法一样来调用它所存…...

《点点之歌》“意外”诞生记
世界是“点点”的,“点点”是世界的。 (笔记模板由python脚本于2024年12月23日 19:28:25创建,本篇笔记适合喜欢诗文的coder翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Free:大咖免费“圣经”教程《 …...
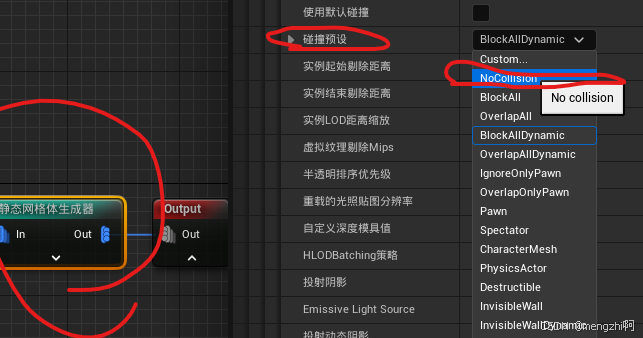
ue5 pcg(程序内容生成)真的简单方便,就5个节点
总结: 前情提示 鼠标单击右键平移节点 1.编辑-》插件-》procedural->勾选两个插件 2.右键-》pcg图表-》拖拽进入场景 3.先看点point 右键-》调试(快捷键d)->右侧设置粒子数 3.1调整粒子数 可以在右侧输入框,使用加减乘除 4.1 表面采样器 …...

32岁前端干了8年,是继续做前端开发,还是转其它工作
前端发展有瓶颈,变来变去都是那一套,只是换了框架换了环境。换了框架后又得去学习,虽然很快上手,但是那些刚毕业的也很快上手了,入门门槛越来越低,想转行或继续卷,该如何破圈 这是一位网友的自述…...
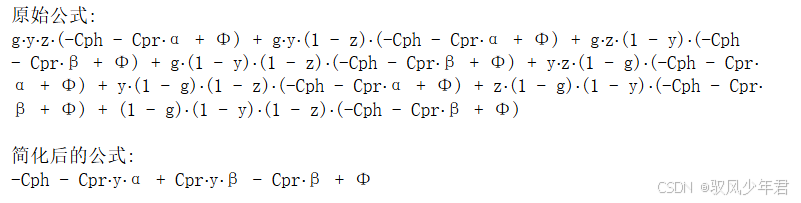
【演化博弈】期望收益函数公式、复制动态方程——化简功能技巧
期望化简 在演化博弈论的研究中,期望收益函数和复制动态方程是核心工具。化简这些公式的功能技巧具有以下几个重要作用: 提高公式的可读性和理解度 复杂的数学表达式可能让人感到困惑。通过化简,公式变得更加简单和易读,使研究者…...

opencv中的各种滤波器简介
在 OpenCV 中,滤波器是图像处理中的重要工具,用于对图像进行平滑、去噪、边缘检测等操作。以下是几种常见滤波器的简单介绍。 1. 均值滤波 (Mean Filter) 功能: 对图像进行平滑处理,减少噪声。 应用场景: 去除图像…...

[Effective C++]条款36-37 两个绝不
本文初发于 “天目中云的小站”,同步转载于此。 条款36 : 绝不重新定义继承而来的non-virtual函数 本条款很容易理解, 援引以前的条款就可以说明为什么 : 条款34中就提到过 : non-virtual函数意味着接口 强制性实现继承, 它不应当被改变. 重新定义继承而来的non-…...
)
各种网站(学习资源及其他)
欢迎围观笔者的个人博客~ 也欢迎通过RSS网址https://kangaroogao.github.io/atom.xml进行订阅~ 大学指南 上海交通大学生存手册中国科学技术大学人工智能与数据科学学院本科进阶指南USTC不完全入学指南大学生活质量指北科研论 信息搜集 AI信息搜集USTC飞跃网站计算机保研 技…...

docker怎么部署高斯数据库
部署高斯数据库(openGauss)到Docker的步骤如下: 安装Docker: 如果您的系统尚未安装Docker,需要先进行安装。以CentOS为例,可以使用以下命令安装Docker: yum install -y docker拉取镜像ÿ…...
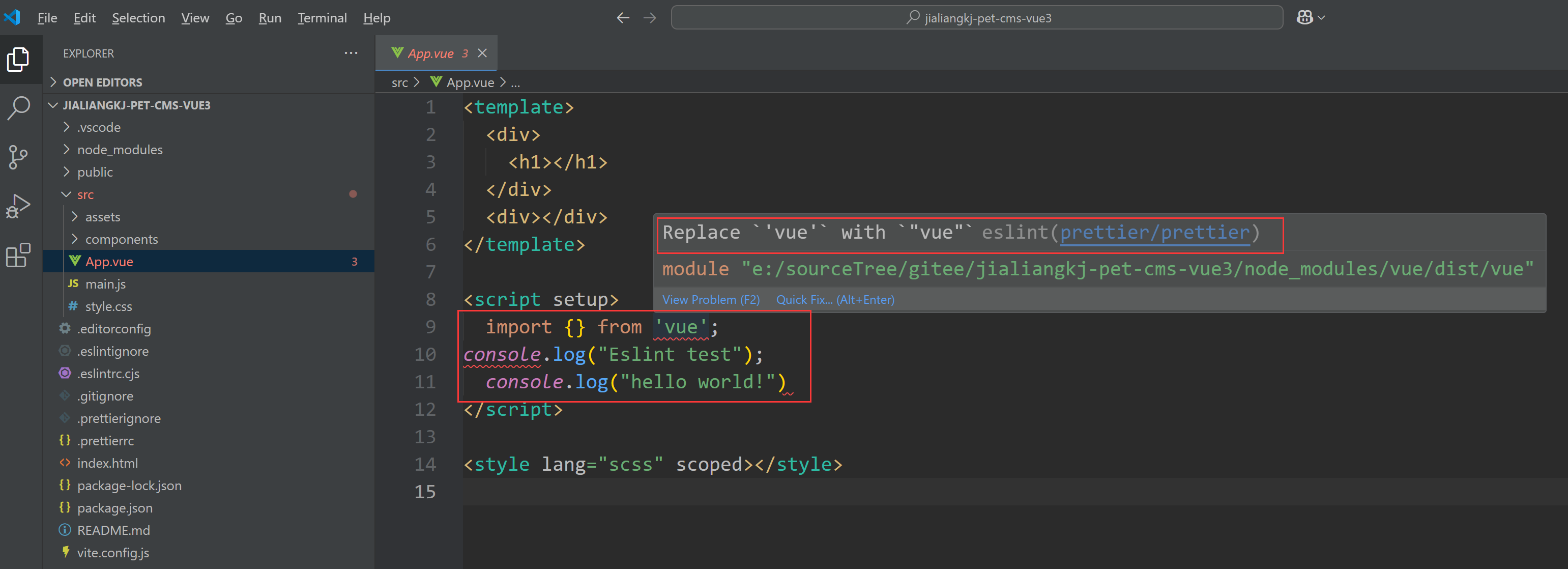
VScode中配置ESlint+Prettier详细步骤(图文详情)
VScode中配置ESlintPrettier详细步骤(图文详情) 前置环境: node 18.19.0 vite 3.2.11 vue 3.2.47 本文将不在演示vue3基础工程创建,如果还没有vue3项目工程请参考文章: Vite创建Vue3工程并引入ElementPlus&#x…...
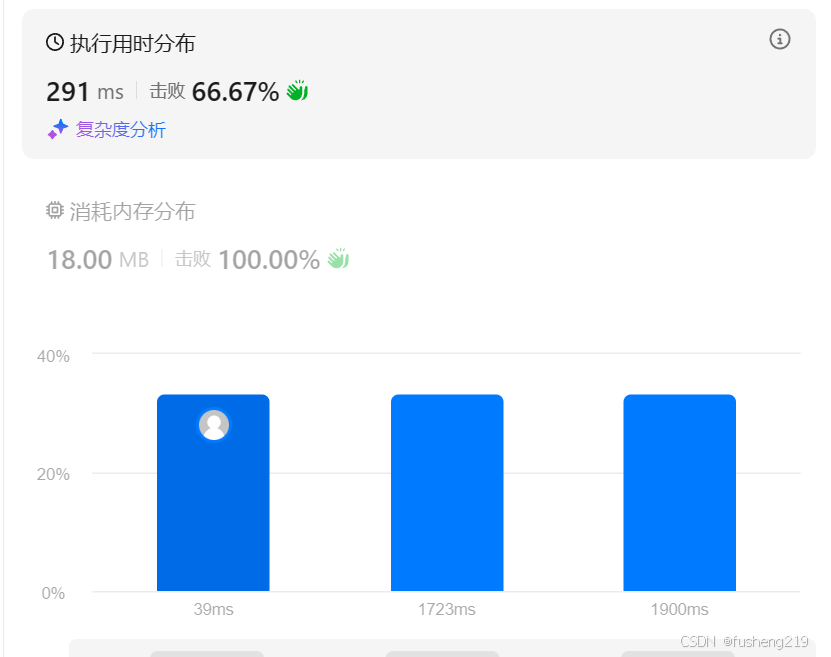
Leetcode打卡:考场就坐
执行结果:通过 题目: 855 考场就坐 在考场里,有 n 个座位排成一行,编号为 0 到 n - 1。 当学生进入考场后,他必须坐在离最近的人最远的座位上。如果有多个这样的座位,他会坐在编号最小的座位上。(另外&am…...
数据库压力测试详解
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 很多人提到 jmeter 时,只会说到 jmeter进行接口自动化或接口性能测试,其实jmeter还能对数据库进行自动化操作。个人常用的场景有以下&#…...

项目测试方案流程详解
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 作为一名软件测试工程师,为项目制作完成的测试方案并执行,是我们日常工作的重要部分,同时,也是一名合格的软件测试工…...
以二进制形式创建gitea仓库
1、官方文档: 数据库准备 | Gitea Documentation 使用二进制文件安装 | Gitea Documentation 2、具体操作 1)创建gitea数据库 2)检查是否安装 Git。要求 Git 版本 > 2.0。 如需升级git请参考以下链接:linux升级git版本-C…...
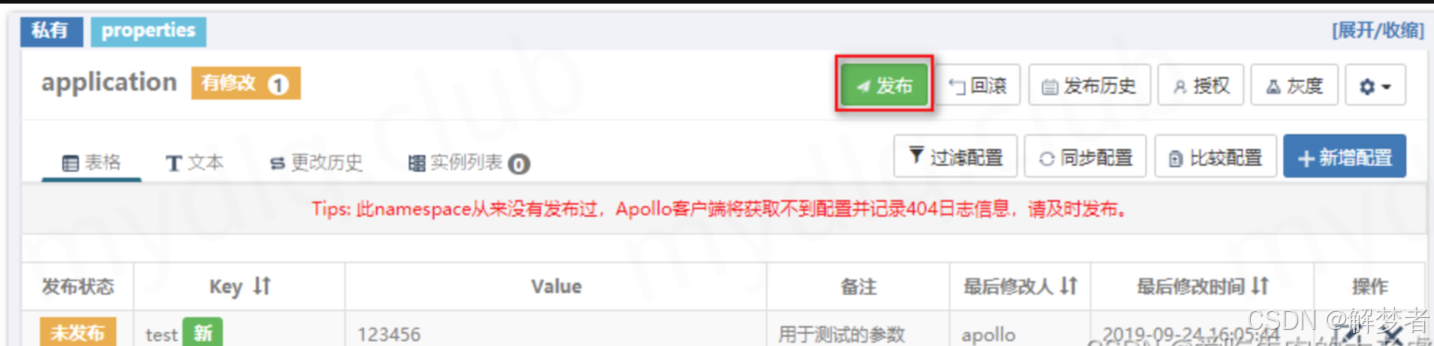
Spring(七)Spring Cloud----Feign、Zuul和Apollo
文章目录 一、服务调用Feign1.1 Feign的基本使用1.2 Feign的属性配置1.2.1 Ribbon配置1.2.2 Hystrix配置 二、网关服务Zuul2.1 Zuul的基本使用2.1.1 请求路由2.1.2 请求过滤 2.2 路由详解2.2.1 传统路由配置2.2.2 服务路由配置2.2.3 服务路由的默认规则2.2.4 自定义路由映射规则…...

*【每日一题 提高题】[蓝桥杯 2022 国 A] 选素数
选素数 小蓝有一个数 x,每次操作小蓝会选择一个小于 x 的素数 p,然后在 x 成为 p 的倍数前不断将 x 加 1,(如果 x 一开始就是 p 的倍数则 x 不变)。 小乔看到了小蓝进行了 2 次上述操作后得到的结果 n,他想…...

华为云环境下LVS/DR架构的故障诊断优化
本文作者:刘涛 文章目录 前言1.LVS/DR集群的问题2.华为云环境3.问题排查3.1 检查LVS/DR模式配置3.1.1 RS服务器3.1.2 DS服务器 3.2 继续分析抓包结果3.2.1 调整tcpdump抓包过滤条件3.2.2 client向集群VIP发包3.2.3 DS服务器arp消息 3.3 查看丢包3.3.1 监控DS和RS服…...

leetcode hot100除自身以外的数组的乘积
238. 除自身以外数组的乘积 已解答 中等 相关标签 相关企业 提示 给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在…...
SQL server学习09-数据库编程(上)
目录 一,了解T-SQL语言 1,常量(标量值) 2,变量 1)局部变量 2)全局变量 二,内置函数 1,字符串函数 2,数学函数 3,日期时间函数 4&#x…...

什么?Flutter 可能会被 SwiftUI/ArkUI 化?全新的 Flutter Roadmap
在刚刚过去的 FlutterInProduction 活动里,Flutter 官方除了介绍「历史进程」和「用户案例」之外,也着重提及了未来相关的 roadmap ,其中就有 3.27 里的 Swift Package Manager 、 Widget 实时预览 和 Dart 与 native 平台原生语言直接互操作…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...
