【路径规划】原理及实现
路径规划(Path Planning)是指在给定地图、起始点和目标点的情况下,确定应该采取的最佳路径。常见的路径规划算法包括A* 算法、Dijkstra 算法、RRT(Rapidly-exploring Random Tree)等。
目录
一.A*
1.算法原理
2.实例
二.Dijkstra
1.算法原理
2.实例
三.RRT
1.算法原理
2.实例
一.A*
A*算法找到的1条由图中节点以及边组成的路径。一般而言,A*算法基于BFS(Breath First Search,广度优先遍历),同时也可以认为是对BFS搜索算法的优化。
1.算法原理
具体执行过程如下:
(1) 搜索区域
以2维平面坐标下的简单搜索为例。

绿色方框代表起点和终点,红色方框代表不可经过的点。
(2) 搜索起点
A*算法从起点开始向四周检索相邻方格并进行扩展,直到扩展扫描到终点,算法结束。
流程如下:
① 从起点S开始,把S作为一个等待检查的方格,将其放入open_list中。
open_list:待走的位置。相当于候选点集合,每到1点,将周围点放入候选集合中,往后有可能往候选点去走。
闭集合:已经走过的位置,不会再被考虑。
② 寻找起点S周围可以到达的方格(最多8个),并将它们加入open_list,同时设置他们的父方格为S;
③ 从open_list中删除起点S,同时将S加入close_list;
④ 计算每个周围方格的F值(F=G+H);
G:从起点S按照生成的路径移动到指定方格的移动代价。有2种距离计算方式:欧拉距离、曼哈顿距离。
H:从指定方格移动到终点的估算成本。使用Manhattan方法,忽略路径中的障碍物,计算当前方格横向或纵向移动到达目标所经过的方格数。
⑤ 从open_list中选取F值最小的方格a,并将其从open_list中删除,放入close_list中;
⑥ 继续检查a的邻接方格:
a). 忽略不可经过的方格以及被标记在close_list中的方格,将剩余的方格加入open_list,并计算这些方格的F值,同时设置父方格为a;
b). 如果某邻接的方格c已经在open_list中,则需计算新的路径从S到c的值G,判断是否需要更新:
如果新的G值更小一些,则修改父方格为方格a,重新计算F值。注意:H值不需要改变,因为方格到达终点的预计消耗是固定的,不需要重复计算。
如果新的G值更大一些,那么说明新路径不是一条更优的路径,则不需要更新值。
⑦ 继续从open_list中找出F值最小的,跳跃至第⑤步继续循环执行。
⑧ 当open_list出现终点E时,代表路径已经被找到,搜索成功。
如果open_list为空,那么说明没有找到合适的路径,搜索失败。
2.实例
'''A*'''
import time
import numpy as np
from matplotlib.patches import Rectangle
import matplotlib.pyplot as plt
import heapq# 地图上的每1个点都是1个Point对象,用于记录该点的类别、代价等信息
class Point:def __init__(self, x=0, y=0):self.x = xself.y = y# 0代表可通行,1代表障碍物self.val = 0 self.cost_g = 0 self.cost_h = 0self.cost_f = 0self.parent = None# 0:不在开集合 1:在开集合 -1:在闭集合self.is_open = 0# 用于heapq小顶堆的比较def __lt__(self, other):return self.cost_f < other.cost_fclass Map:def __init__(self, map_size):self.map_size = map_sizeself.width = map_size[0]self.height = map_size[1]self.map = [[Point(x, y) for y in range(self.map_size[1])] for x in range(self.map_size[0])]# 手动设置障碍物,可多次调用设置地图def set_obstacle(self, topleft, width, height):for x in range(topleft[0], topleft[0] + width):for y in range(topleft[1], topleft[1] + height):self.map[x][y].val = 1class AStar:def __init__(self, map, start_point, end_point, connect_num=4):self.map: Map = mapself.start_point = start_pointself.end_point = end_point# 开集合,先放入起点,从起点开始遍历self.open_set = [self.start_point]self.start_point.is_open = 1 # 连通数,目前支持4连通或8连通 self.connect_num = connect_numself.diffuse_dir = [(1, 0), (-1, 0), (0, 1), (0, -1)]def g_cost(self, p):'''计算 g 代价:当前点与父节点的距离 + 父节点的 g 代价(欧氏距离)'''x_dis = abs(p.parent.x - p.x)y_dis = abs(p.parent.y - p.y)return np.sqrt(x_dis ** 2 + y_dis ** 2) + p.parent.cost_gdef h_cost(self, p):'''计算 h 代价:当前点与终点之间的距离(欧氏距离)'''x_dis = abs(self.end_point.x - p.x)y_dis = abs(self.end_point.y - p.y)return np.sqrt(x_dis ** 2 + y_dis ** 2)def is_valid_point(self, x, y):# 无效点:超出地图边界或为障碍物if x < 0 or x >= self.map.width:return Falseif y < 0 or y >= self.map.height:return Falsereturn self.map.map[x][y].val == 0def search(self):self.start_time = time.time()p = self.start_pointwhile not (p == self.end_point):# 弹出代价最小的开集合点,若开集合为空,说明没有路径try:p = heapq.heappop(self.open_set)except:raise 'No path found, algorithm failed!!!'p.is_open = -1# 遍历周围点for i in range(self.connect_num):dir_x, dir_y = self.diffuse_dir[i]self.diffusion_point(p.x + dir_x, p.y + dir_y, p)return self.build_path(p) # p = self.end_pointdef diffusion_point(self, x, y, parent):# 无效点或者在闭集合中,跳过if not self.is_valid_point(x, y) or self.map.map[x][y].is_open == -1:returnp = self.map.map[x][y]pre_parent = p.parentp.parent = parent# 先计算出当前点的总代价cost_g = self.g_cost(p)cost_h = self.h_cost(p)cost_f = cost_g + cost_h# 如果在开集合中,判断当前点和开集合中哪个点代价小,换成小的,相同x,y的点h值相同,g值可能不同if p.is_open == 1:if cost_f < p.cost_f:# 如果从当前parent遍历过来的代价更小,替换成当前的代价和父节点p.cost_g, p.cost_h, p.cost_f = cost_g, cost_h, cost_felse:# 如果从之前父节点遍历过来的代价更小,保持之前的代价和父节点p.parent = pre_parentelse:# 如果不在开集合中,说明之间没遍历过,直接加到开集合里就好p.cost_g, p.cost_h, p.cost_f = cost_g, cost_h, cost_fheapq.heappush(self.open_set, p)p.is_open = 1def build_path(self, p):print('search time: ', time.time() - self.start_time, ' seconds')# 回溯完整路径path = []while p != self.start_point:path.append(p)p = p.parentprint('search time: ', time.time() - self.start_time, ' seconds')# 打印开集合、闭集合的数量print('open set count: ', len(self.open_set))close_count = 0for x in range(self.map.width):for y in range(self.map.height):close_count += 1 if self.map.map[x][y].is_open == -1 else 0print('close set count: ', close_count)print('total count: ', close_count + len(self.open_set))# path = path[::-1] # path为终点到起点的顺序,可使用该语句翻转return pathif __name__ == '__main__':map = Map((6, 6))# 用于显示plt图ax = plt.gca()ax.xaxis.set_ticks_position('top')ax.set_xlim([0, map.width])ax.set_ylim([0, map.height])plt.tight_layout()plt.grid(True, linestyle="--", color="black", linewidth="1", axis='both')ax.xaxis.set_ticks_position('top')ax.invert_yaxis()# 设置障碍物map.set_obstacle([2, 2], 3, 1)map.set_obstacle([2, 3], 1, 2)# 设置起始点和终点,并创建astar对象start_point = map.map[1][1]end_point = map.map[4][4]# 将障碍物及起点、终点显示到plt上ax.add_patch(Rectangle([2, 2], width=3, height=1, color='red'))ax.add_patch(Rectangle([2, 3], width=1, height=2, color='red'))ax.add_patch(Rectangle([1, 1], width=1, height=1, color='green'))ax.add_patch(Rectangle([4, 4], width=1, height=1, color='green'))astar = AStar(map, start_point, end_point)path = astar.search()# 可视化起点到终点完整路径for p in path:if p!=end_point:ax.add_patch(Rectangle([p.x, p.y], width=1, height=1, color='blue'))plt.savefig('res.jpg') plt.show()
二.Dijkstra
Dijkstra是1种适用于非负权值网络的单源最短路径算法,可以给出从指定节点到图中其他节点的最短路径,以及任意2点的最短路径。
1.算法原理
下面用1个示例讲述算法的原理过程,如图所示,1个有向权值图,利用Dijkstra算法找到从节点1到节点6的最短路径。

(1) 首先进行初始化,初始化1个空的open list,close list 以及parent。将起点及其距离信息放入到open list 中,将起点及其父亲节点放入parent中,起点的父节点为None。
open list :存放已经访问的从该节点到起点有路径的结点(有路径但不一定是最优路径)
close list :存放那些已经找到最优路径的结点。
parent :存放结点的父子关系,方便后面路径回溯。

(2) 按步骤执行:

(3) 按步骤执行:

(4) 按步骤执行:

(5) 按步骤执行:

(6) 按步骤执行:

(7) 按步骤执行:

(8) 路径回溯
根据parent中的继承关系,从终点向起点回溯,得到从起点到终点的最短路径为:1=>4=>7=>6,最短路径长为:6。
2.实例
import heapqdef dijkstra(graph,start):distances = {vertex: float('infinity') for vertex in graph}distances[start] = 0# 初始化父亲节点parent = {vertex: None for vertex in graph}priority_queue = [(0,start)]while priority_queue:# 弹出堆中距离最小的节点current_distance, current_vertex = heapq.heappop(priority_queue)# 如果当前距离已经大于已知的最短距离,则跳过if current_distance > distances[current_vertex]:continue# 更新相邻节点的距离for neighbor, weight in graph[current_vertex].items():distance = current_distance + weight# 如果找到更短的路径,则更新距离,并将节点加入优先队列if distance < distances[neighbor]:distances[neighbor] = distanceparent[neighbor] = current_vertexheapq.heappush(priority_queue, (distance, neighbor))# print("加入后的队列:",priority_queue)return distances, parent# 输出路径回溯
def get_path(parent,end):path = []current = endwhile current is not None:path.append(current)current = parent[current]path.reverse()return pathgraph = {'1': {'2': 2, '4': 1},'2': {'4': 3, '5': 11 },'3': {'1': 4, '6': 5},'4': {'5': 2, '6': 8, '7': 4},'5': {'7': 6},'6':{},'7': {'6': 1},
}
start_node='1'
end_node = '6'
distances, parent = dijkstra(graph, start_node)
path = get_path(parent, end_node)
print(f"从节点 {start_node} 到节点 {end_node} 的路径:", path)
三.RRT
1.算法原理
快速随机树算法(Rapid Random Tree,RRT)以初始的1个根节点,通过随机采样的方法在空间搜索,然后添加叶节点来不断扩展随机树。当目标点进入随机树里面后,随机树扩展立即停止,此时能找到1条从起始点到目标点的路径。
算法的计算过程如下:
(1) 初始化随机树。设置起点,目标点
和搜索空间
;将起点作为随机树搜索的起点,此时树中只包含1个节点即根节点;
(2)在中随机采样。在
中随机采样1个点
,若
不在障碍物范围内,则计算随机树中所有节点到
的欧式距离,并找到距离最近的节点
;若
在障碍物范围内则重新采样;
(3)生成新节点。在和
连线方向,由固定步长距离生成1个新的节点
,并判断
是否在障碍物范围内,若不在障碍物范围内则将
添加到随机树中,并将
的父节点设置为
;否则的话返回(2)重新对环境进行随机采样;
(4)停止搜索。重复步骤(2)、(3),当和
之间的距离小于设定的阈值时,则代表随机树已经到达了目标点,将作为最后1个路径节点加入到随机树中,算法结束并得到所规划的路径 。
2.实例
import math
import random
import matplotlib.pyplot as plt
import numpy as np
from celluloid import Cameraclass RRT:class Node:def __init__(self, x, y):self.x = xself.y = yself.path_x = []self.path_y = []self.parent = Noneclass AreaBounds:def __init__(self, area):self.xmin = float(area[0])self.xmax = float(area[1])self.ymin = float(area[2])self.ymax = float(area[3])def __init__(self,start,goal,obstacle_list,rand_area,expand_dis=1.0,goal_sample_rate=5,max_iter=500,play_area=None,robot_radius=0.0,):"""Setting Parameterstart:起点 [x,y]goal:目标点 [x,y]obstacleList:障碍物位置列表 [[x,y,size],...]rand_area: 采样区域 x,y ∈ [min,max]play_area: 约束随机树的范围 [xmin,xmax,ymin,ymax]robot_radius: 机器人半径expand_dis: 扩展的步长goal_sample_rate: 采样目标点的概率,百分制.default: 5,即表示5%的概率直接采样目标点"""self.start = self.Node(start[0], start[1]) # 根节点(0,0)self.end = self.Node(goal[0], goal[1]) # 终点(6,10)self.min_rand = rand_area[0] # -2 树枝生长区域xminself.max_rand = rand_area[1] # 15 xmaxif play_area is not None:self.play_area = self.AreaBounds(play_area) # 树枝生长区域,左下(-2,0)==>右上(12,14)else:self.play_area = None # 数值无限生长self.expand_dis = expand_dis # 树枝一次的生长长度self.goal_sample_rate = goal_sample_rate # 多少概率直接选终点self.max_iter = max_iter # 最大迭代次数self.obstacle_list = obstacle_list # 障碍物的坐标和半径self.node_list = [] # 保存节点self.robot_radius = robot_radius # 随机点的搜索半径# 路径规划def planning(self, animation=True, camara=None):# 先在节点列表中保存起点self.node_list = [self.start]for i in range(self.max_iter):# 随机选取一个节点rnd_node = self.sample_free()# 从已知节点中选择和目标节点最近的节点nearest_ind = self.get_nearest_node_index(self.node_list, rnd_node)nearest_node = self.node_list[nearest_ind]new_node = self.steer(nearest_node, rnd_node, self.expand_dis)# 判断新点是否在规定的树的生长区域内,新点和最近点之间是否存在障碍物if self.is_inside_play_area(new_node, self.play_area) and \self.obstacle_free(new_node, self.obstacle_list, self.robot_radius):# 都满足才保存该点作为树节点self.node_list.append(new_node)# 如果此时得到的节点到目标点的距离小于扩展步长,则直接将目标点作为xrand。if self.calc_dist_to_goal(self.node_list[-1].x, self.node_list[-1].y) <= self.expand_dis:# 以新点为起点,向终点画树枝final_node = self.steer(self.node_list[-1], self.end, self.expand_dis)# 如果最新点和终点之间没有障碍物Trueif self.obstacle_free(final_node, self.obstacle_list, self.robot_radius):return self.generate_final_course(len(self.node_list) - 1)if animation and i % 5 == 0:self.draw_graph(rnd_node, camara)return None # cannot find path# 距离最近的已知节点坐标,随机坐标,从已知节点向随机节点的延展的长度def steer(self, from_node, to_node, extend_length=float("inf")):# d已知点和随机点之间的距离,theta两个点之间的夹角d, theta = self.calc_distance_and_angle(from_node, to_node)# 如果树枝的生长长度超出了随机点,就用随机点位置作为新节点if extend_length >= d:new_x = to_node.xnew_y = to_node.y# 如果树生长长度没达到随机点长度,就截取长度为extend_length的节点作为新节点else:new_x = from_node.x + math.cos(theta) * extend_lengthnew_y = from_node.y + math.sin(theta) * extend_lengthnew_node = self.Node(new_x, new_y)new_node.path_x = [from_node.x]new_node.path_y = [from_node.y]new_node.path_x.append(new_x)new_node.path_y.append(new_y)new_node.parent = from_nodereturn new_nodedef generate_final_course(self, goal_ind):path = [[self.end.x, self.end.y]]node = self.node_list[goal_ind]while node.parent is not None:path.append([node.x, node.y])node = node.parentpath.append([node.x, node.y])return pathdef calc_dist_to_goal(self, x, y):"""计算(x,y)离目标点的距离"""dx = x - self.end.xdy = y - self.end.yreturn math.hypot(dx, dy)def sample_free(self):if random.randint(0, 100) > self.goal_sample_rate:rnd = self.Node(random.uniform(self.min_rand, self.max_rand),random.uniform(self.min_rand, self.max_rand))else: # goal point samplingrnd = self.Node(self.end.x, self.end.y)return rnd# 绘制搜索过程def draw_graph(self, rnd=None, camera=None):if camera == None:plt.clf()# for stopping simulation with the esc key.plt.gcf().canvas.mpl_connect('key_release_event',lambda event: [exit(0) if event.key == 'escape' else None])# 画随机点if rnd is not None:plt.plot(rnd.x, rnd.y, "^k")if self.robot_radius > 0.0:self.plot_circle(rnd.x, rnd.y, self.robot_radius, '-r')# 画生成的树for node in self.node_list:if node.parent:plt.plot(node.path_x, node.path_y, "-g")# 画障碍物for (ox, oy, size) in self.obstacle_list:self.plot_circle(ox, oy, size)# 画出可行区域if self.play_area is not None:plt.plot([self.play_area.xmin, self.play_area.xmax,self.play_area.xmax, self.play_area.xmin,self.play_area.xmin],[self.play_area.ymin, self.play_area.ymin,self.play_area.ymax, self.play_area.ymax,self.play_area.ymin],"-k")# 画出起点和目标点plt.plot(self.start.x, self.start.y, "xr")plt.plot(self.end.x, self.end.y, "xr")plt.axis("equal")plt.axis([-2, 15, -2, 15])plt.grid(True)plt.pause(0.01)if camera != None:camera.snap()@staticmethoddef plot_circle(x, y, size, color="-b"):deg = list(range(0, 360, 5))deg.append(0)xl = [x + size * math.cos(np.deg2rad(d)) for d in deg]yl = [y + size * math.sin(np.deg2rad(d)) for d in deg]plt.plot(xl, yl, color)@staticmethoddef get_nearest_node_index(node_list, rnd_node):# 计算所有已知节点和随机节点之间的距离dlist = [(node.x - rnd_node.x) ** 2 + (node.y - rnd_node.y) ** 2for node in node_list]minind = dlist.index(min(dlist))return minind@staticmethoddef is_inside_play_area(node, play_area):if play_area is None:return Trueif node.x < play_area.xmin or node.x > play_area.xmax or \node.y < play_area.ymin or node.y > play_area.ymax:return Falseelse:return True@staticmethoddef obstacle_free(node, obstacleList, robot_radius):# 目标点,障碍物中点和半径,移动时的占地半径if node is None:return Falsefor (ox, oy, size) in obstacleList:dx_list = [ox - x for x in node.path_x]dy_list = [oy - y for y in node.path_y]d_list = [dx * dx + dy * dy for (dx, dy) in zip(dx_list, dy_list)]if min(d_list) <= (size + robot_radius) ** 2:return Falsereturn True@staticmethoddef calc_distance_and_angle(from_node, to_node):"""计算两个节点间的距离和方位角"""dx = to_node.x - from_node.xdy = to_node.y - from_node.yd = math.hypot(dx, dy)theta = math.atan2(dy, dx)return d, thetadef main(gx=6.0, gy=10.0):print("start " + __file__)fig = plt.figure(1)camera = Camera(fig) # 保存动图时使用show_animation = TrueobstacleList = [(5, 5, 1), (3, 6, 2), (3, 8, 2), (3, 10, 2), (7, 5, 2),(9, 5, 2), (8, 10, 1)] # [x, y, radius]# Set Initial parametersrrt = RRT(start=[0, 0],goal=[12, 12],rand_area=[-2, 15],obstacle_list=obstacleList,play_area=[-2, 15, 0, 15],# 搜索半径robot_radius=0.2)path = rrt.planning(animation=show_animation, camara=camera)if path is None:print("Cannot find path")else:print("found path!!")# 绘制最终路径if show_animation:print('start drawing the final path')rrt.draw_graph(camera=camera)plt.grid(True)plt.pause(0.01)plt.plot([x for (x, y) in path], [y for (x, y) in path], '-r')if camera != None:camera.snap()animation = camera.animate()animation.save('trajectory_res.gif')plt.show()if __name__ == '__main__':main()
相关文章:
【路径规划】原理及实现
路径规划(Path Planning)是指在给定地图、起始点和目标点的情况下,确定应该采取的最佳路径。常见的路径规划算法包括A* 算法、Dijkstra 算法、RRT(Rapidly-exploring Random Tree)等。 目录 一.A* 1.算法原理 2.实…...

【AIGC】ChatGPT 结构化 Prompt 的高级应用
博客主页: [小ᶻ☡꙳ᵃⁱᵍᶜ꙳] 本文专栏: AIGC | ChatGPT 文章目录 💯前言💯标识符的使用(Use of Identifiers)1. #2. <>3. - 或 4. [] 💯属性词的重要性和应用应用场景 💯具体模块…...

Go web 开发框架 Iris
背景 掌握了 Go 语言的基础后就该开始实践了,编写Web应用首先需要一个 web 开发框架。做框架选型时,处理web请求是基本功能,至于MVC是更进一步需要。现在比较流行的web架构是前后端分离,后端响应RESTful的请求,Iris 能…...

uniapp Native.js 调用安卓arr原生service
最近搞了个uni小项目,一个定制的小平板,带一个nfc设备,厂家只给了一套安卓原生demo,头一次玩原生安卓,废了好半天劲打出来arr包,想镶进uniapp里,网上查了好久,都是错的,要…...

C#代码实现把中文录音文件(.mp3 .wav)转为文本文字内容
我们有一个中文录音文件.mp3格式或者是.wav格式,如果我们想要提取录音文件中的文字内容,我们可以采用以下方法,不需要使用Azure Speech API 密钥注册通过离线的方式实现。 1.首先我们先在NuGet中下载两个包 NAudio 2.2.1、Whisper.net 1.7.3…...

【一文了解】C#重点-委托1
本篇文章来学习一下C#的委托,委托是C#中的一个重要概念,它允许将方法作为参数传递给其他方法。C#中的委托类似于C或C中的函数指针,并且类型安全。 委托 1.委托的定义 委托(delegate)是方法的代理/代表,委托…...

WPF+MVVM案例实战与特效(四十五)- 打造优雅交互:ListBox 的高级定制与行为触发(侧边菜单交互面板)
文章目录 1、引言2、案例效果3、案例实现1、依赖安装2、文件创建3、代码实现1、依赖引用与上下文2、个性化视觉效果:自定义 ItemContainerStyle3、页面样式与布局完整代码4、ViewModel 逻辑实现5、子界面代码:3、实现效果4、源代码获取5、总结1、引言 在WPF应用程序开发中,…...

新版Android Studio 2024.1.2版本,如何通过无线wifi连接手机实现交互
1、首先,先确定手机是否启动了开发者选项 在我的设备 -> 全部参数 -> MIUI版本点击6下 (有的手机是 关于手机 -> 查看手机版本 ) 2、在设置中搜索 开启开发者选项 3、进入开发者选项后,在 调试 中选择 无线调试并选择…...

VTK知识学习(26)- 图像基本操作(一)
1、前言 图像处理离不开一些基本的图像数据操作,例如获取和修改图像的基本信息、访问和修改图像像素值、图像显示、图像类型转换等。熟练掌握这些基本操作有助于使用 VTK进行图像处理应用程序的快速开发。 2、图像信息的访问与修改 1)利用vtkIamgeData…...

2024年9月AI头条新闻:创新与挑战并存
2024年9月AI头条新闻:创新与挑战并存 9月,人工智能领域继续高速发展,重大产品发布、伦理争议和技术突破交织在一起。让我们回顾一下本月最重要的AI新闻: OpenAI的o1:更强大的语言模型 OpenAI推出了o1,一个…...
[Xshell] Xshell的下载安装使用、连接linux、 上传文件到linux系统-详解(附下载链接)
前言 xshell 链接:https://pan.quark.cn/s/57062561e81a 提取码:TK4K 链接失效(可能被官方和谐)可评论或私信我重发 安装 下载后解压得到文件 安装路径不要有中文 打开文件 注意!360等软件会拦截创建注册表的行为&a…...

count(1)、count(_)与count(列名)的区别?
大家好,我是锋哥。今天分享关于【count(1)、count(_)与count(列名)的区别?】面试题。希望对大家有帮助; count(1)、count(_)与count(列名)的区别? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 在 SQL 中,…...

代码随想录训练营第二十七天| 贪心理论基础 455.分发饼干 376. 摆动序列 53. 最大子序和
贪心没有套路,说白了就是常识性推导加上举反例 今天的内容比较简单 简单了解贪心是通过局部最优解反推全局最优解(有经验成分) 455.分发饼干 题目链接:455. 分发饼干 - 力扣(LeetCode) 讲解链接ÿ…...

List直接使用removeAll报错
List直接使用removeAll报错 需要先将list转换才能使用 原因是: removeAll 方法在 Java 中用于从当前列表中删除另一个列表中存在的所有元素。如果直接对 List 接口的一个实现使用 removeAll 方法抛出异常,可能的原因有: 不同的List实现&am…...

Debian环境安装Docker Engine
Debian环境安装Docker Engine 卸载旧版本使用APT工具安装Docker设置存储库安装Docker设置权限 docker compose命令卸载Docker 卸载旧版本 要卸载的非官方软件包是: docker.iodocker-composedocker-docpodman-docker 此外,Docker Engine 依赖 containe…...

Python常用内置函数总结
目录 1. abs() 2. complex() 3. divmod() 4. eval() 5. float() 6. hash() 7. input() 8. int() 9. len() 10. list() 11. oct() 12. open() 13. pow() 14. print() 15. range() 16. reversed() 17. round() 18. sorted()…...

深入了解蓝牙Profile类型与设备的对应关系
在现代技术中,蓝牙作为一种无线通信技术,广泛应用于各种设备之间的短距离通信。不同的设备在连接时使用不同的蓝牙Profile(配置文件),每种Profile都为特定的设备功能提供支持,例如音频流传输、语音通话、文件传输等。在本文中,我们将详细介绍蓝牙Profile的常见类型及其对…...
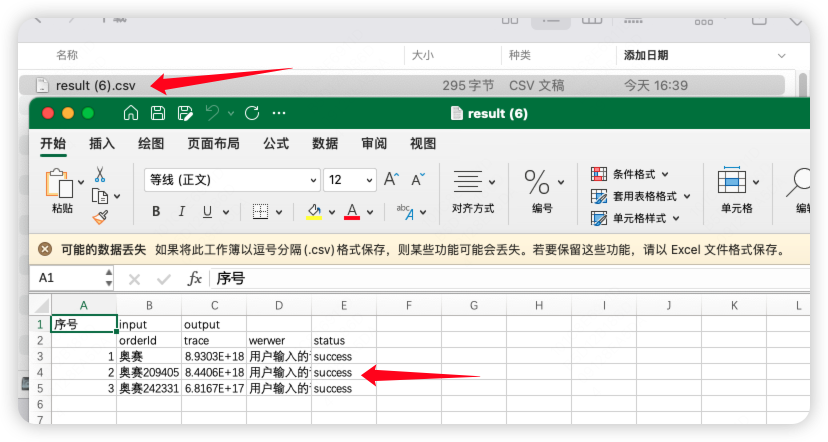
[bug]java导出csv用Microsoft Office Excel打开乱码解决
[bug]java导出csv用Microsoft Office Excel打开乱码 现象 首先这个csv文件用macbook自带的 "Numbers表格" 软件打开是不乱码的, 但是使用者是Windows系统,他的电脑没有"Numbers表格"工具, 他用Microsoft Office Excel打开之后出现乱码,如下图…...

2023年区块链职业技能大赛——区块链应用技术(一)模块一
模块一:区块链产品方案设计及系统运维: 任务1-1:区块链产品需求分析与方案设计 1.依据给定区块链食品溯源系统的业务架构图,对考题进行业务分析,可能多的去考虑一个业务系统所需要的模块,使用Visio或思维导图工具展现本系统的基本设计概念和…...

4 软件工程——总体设计
一、设计过程 1.两个主要阶段 系统设计阶段:确定系统的具体实现方案结构设计阶段:确定软件结构 2.九个步骤 设想供选择的方案选取合理的方案推荐最佳方案功能分解设计软件结构设计数据库制定测试计划书写文档审查和复审 二、设计原理 1.模块化 模块…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
