贪心算法(常见贪心模型)


常见贪心模型
简单排序模型
最小化战斗力差距


题目分析:


#include <bits/stdc++.h>
using namespace std;const int N = 1e5 + 10;int n;
int a[N];int main()
{// 请在此输入您的代码cin >> n;for (int i = 1;i <= n;i++) cin >> a[i];sort(a+1,a+1+n);int disparity = 1e9-1;for (int i = 1;i < n;i++) disparity = min(disparity,a[i+1] - a[i]);cout << disparity << '\n';return 0;
}货仓选址



可以发现,仓库建在中间,可以使得货仓到每家商店的距离之和最小
#include <bits/stdc++.h>
using namespace std;const int N = 100010;int n;
int a[N];int main()
{cin >> n;for (int i = 1;i <= n;i++) cin >> a[i];sort(a+1,a+1+n);int store = a[n/2 + 1];int res = 0;for (int i = 1;i <= n;i++) {if (i == n/2 + 1) continue;res += abs(store - a[i]);}cout << res << '\n';return 0;
}总操作一定的情况下的最小代价模型
谈判



如果每次选择代价最小的两个部落合并,不仅可以使得当前代价最小,还可以使得后续合并的代价也尽可能小
局部最优 ==》全局最优
用数组模拟(O(n^2 log n))
#include <bits/stdc++.h>
using namespace std;const int N = 1010;int n;
int a[N];int main()
{// 先排序 找到两个人数最少的部落cin >> n;for (int i = 1;i <= n;i++) cin >> a[i];sort(a+1,a+1+n);int sum = 0;for (int i = 2;i <= n;i++) {a[i] = a[i] + a[i-1];sum += a[i];sort(a+i,a+1+n);}cout << sum << '\n';return 0;
}用优先级队列实现
#include <bits/stdc++.h>
using namespace std;
using ll = long long;priority_queue<ll,vector<ll>,greater<ll>> pq;int main()
{//用优先队列实现 每次取其中两个代价最小的部落进行合并,总花费最小int n;cin >> n;for (int i = 1;i <= n;i++){ll x;cin >> x;pq.push(x);} ll ans = 0;while (pq.size() > 1){ll x = pq.top();pq.pop();ll y = pq.top();pq.pop();ans += x+y;pq.push(x+y);}cout << ans << '\n';return 0;
}糖果传递





#include <bits/stdc++.h>
using namespace std;
using ll = long long;const int N = 1000010;int n;
int a[N];
ll c[N];int main()
{cin >> n;ll sum = 0;for (int i = 1;i <= n;i++) cin >> a[i],sum += a[i];int avg = sum / n;for (int i = n;i > 0;i--) c[i] = c[i+1] + avg - a[i];c[1] = 0;sort(c+1,c+1+n);ll res = 0;for (int i = 1;i <= n;i++) res += abs(c[i] - c[(n+1)/2]);cout << res << '\n';return 0;
}最少数量的贪心模型
纪念品分组



为了让组数最少,我们要尽可能将两个纪念品打包成一组
怎样的两个纪念品最有可能打包成一组呢,无疑是一个大和一个小的
所以我们先去找最大和最小的,如果不能打包,则去找次小的,直到能打包成一组
不能打包的大的纪念品则单独一组
#include <bits/stdc++.h>
using namespace std;const int N = 30010;int w,n;
int a[N];int main()
{// 请在此输入您的代码cin >> w >> n;int cnt = 0;for (int i = 1;i <= n;i++) cin >> a[i];sort(a+1,a+1+n);for (int i = 1,j = n;;){if (i > j) break;if (a[i] + a[j] <= w){cnt++;i++,j--;}else {j--;cnt++;}}cout << cnt << '\n';return 0;
}找规律的贪心模型

分糖果


我们要去使得所有糖果组成的字符串中字典序最大的字符串尽可能小
字符串字典集大小先看首字母大小,其次看后面的字母大小
a < b < c ...
a < aabs...
先给字符串排序,然后分为三类讨论
1️⃣字符串全相等(假设全a),那就尽量使得每个人分到的字符串的最大长度尽可能小,即平分字符串
2️⃣s[x] == s[1] 说明第x个是最小的字符,让它带着后面所有的字符一起输出即可
3️⃣ s[x] != s[1] ,后面一坨字符直接丢到s[1]后面,分给 第一个同学即可
#include <bits/stdc++.h>
using namespace std;const int N = 1e6 + 10;int n,x;
char s[N];int main()
{// 请在此输入您的代码cin >> n >> x;cin >> s+1;sort(s+1,s+1+n);if (s[1] == s[n]) {for (int i = 1;i <= n / x + (n % x ? 1 : 0);i++) cout << s[i];}else if (s[1] == s[x]) {for (int i = x;i <= n;i++) cout << s[i];}else {cout << s[x];}return 0;
}股票买卖II



容易发现规律,如果后一天的股票比当天高,那么就今天买入后一天卖出
#include <bits/stdc++.h>
using namespace std;const int N = 1e5 + 10;int n;
int a[N];int main() {cin >> n;for (int i = 1;i <= n;i++) cin >> a[i];int res = 0;for (int i = 1;i <= n;i++){if (a[i] < a[i+1]) res += a[i+1] - a[i];}cout << res << '\n';return 0;
}乘积最大






#include <bits/stdc++.h>
using namespace std;
using ll = long long;const int N = 1e5 + 10,mod = 1000000009;int n,k;
int a[N];int main()
{cin >> n >> k;for (int i = 1;i <= n;i++) cin >> a[i];sort(a+1,a+1+n);int res = 1;int l = 1,r = n;int sign = 1;if (k % 2) {res = a[r--];k--;if (res < 0) sign = -1;}while (k){ll x = (ll)a[l] * a[l+1],y = (ll)a[r] * a[r-1];if (x * sign > y * sign){res = x % mod * res % mod;l += 2;}else {res = y % mod * res % mod;r -= 2;}k -= 2;}cout << res << endl;return 0;
}相关文章:

贪心算法(常见贪心模型)
常见贪心模型 简单排序模型 最小化战斗力差距 题目分析: #include <bits/stdc.h> using namespace std;const int N 1e5 10;int n; int a[N];int main() {// 请在此输入您的代码cin >> n;for (int i 1;i < n;i) cin >> a[i];sort(a1,a1n);…...

git自动压缩提交的脚本
可以将当前未提交的代码自动执行 git addgit commitgit squash Git 命令安装指南 1. 创建脚本目录 如果目录不存在,创建它: mkdir -p ~/.local/bin2. 创建脚本文件 vim ~/.local/bin/git-squash将完整的脚本代码复制到此文件中。 3. 设置脚本权限…...

Kinova在开源家庭服务机器人TidyBot++研究里大展身手
在科技日新月异的今天,机器人技术在家庭场景中的应用逐渐成为现实,改变着我们的生活方式。今天,我们将深入探讨一篇关于家用机器人研究的论文,剖析其中的创新成果, 论文引用链接:http://tidybot2.github.i…...

使用 Spring Boot 实现文件上传:从配置文件中动态读取上传路径
使用 Spring Boot 实现文件上传:从配置文件中动态读取上传路径 一、前言二、文件上传的基本概念三、环境准备1. 引入依赖2. 配置文件设置application.yml 配置示例:application.properties 配置示例: 四、编写文件上传功能代码1. 控制器类2. …...

《鸿蒙HarmonyOS应用开发从入门到精通(第2版)》学习笔记——HarmonyOS技术理念
1.2 技术理念 在万物智联时代重要机遇期,HarmonyOS结合移动生态发展的趋势,提出了三大技术理念(如下图3-1所示):一次开发,多端部署;可分可合,自由流转;统一生态…...

将多个 k8s yaml 配置文件合并为一个文件
如下bash脚本实现功能 “将多个k8s的yaml 配置文件” 合并为一个 yaml,使用 --- 分割文件配置。 创建文件 merge_yaml.sh ,内容如下: #!/bin/bash# 默认参数 input_patterns() # 匹配的文件模式数组 output_file"combined.yaml"…...

Linux 文件的特殊权限—Sticky Bit(SBIT)权限
本文为Ubuntu Linux操作系统- 第十九期~~ 其他特殊权限: 【SUID 权限】和【SGID 权限】 更多Linux 相关内容请点击👉【Linux专栏】~ 主页:【练小杰的CSDN】 文章目录 Sticky(SBIT)权限基本概念Sticky Bit 的表示方式举例 设置和取…...

MIPI D-PHY/C-PHY/M-PHY 高速串行接口标准
MIPI D-PHY、C-PHY和M-PHY都是MIPI联盟制定的高速串行接口标准。它们都具有低功耗、高速传输速率等特点,但各有侧重: ➢MIPI D-PHY:适用于手机与其他设备之间的数据传输。 ➢MIPI C-PHY:专为手机摄像头而设计。 ➢MIPI M-PHY&am…...

USB免驱IC读写器QT小程序开发
USB免驱全协议IC卡读写器QT小程序开发,读取15693卡。 QT小程序UI开发界面: QT程序代码mainWindow.cpp代码如下: MainWindow::MainWindow(QWidget *parent): QMainWindow(parent), ui(new Ui::MainWindow) {ui->setupUi(this); }MainWind…...

OSCP靶场训练冒险之kioprix4:shell逃逸以及利用数据库提权
声明! 学习资源来自B站up主 **泷羽sec** 有兴趣的师傅可以关注一下,如涉及侵权马上删除文章,笔记只是方便各位师傅的学习和探讨,文章所提到的网站以及内容,只做学习交流,其他均与本人以及泷羽sec团队无关&a…...

NIPS2014 | GAN: 生成对抗网络
Generative Adversarial Nets 摘要-Abstract引言-Introduction相关工作-Related Work对抗网络-Adversarial Nets理论结果-Theoretical Results实验-Experiments优势和不足-Advantages and disadvantages缺点优点 结论及未来工作-Conclusions and future work研究总结未来研究方…...

Postman接口测试01|接口测试基础概念、http协议、RESTful风格、接口文档
目录 一、接口测试基础概念 1、什么是接口 2、接口的类型 3、什么是接口测试 4、为什么要做接口测试 5、接口测试的实现方式 6、什么是自动化接口测试? 二、接口返回的数据格式 1、三种格式 2、Json 三、接口协议 1、webservice协议 2、dubbo协议 3、…...

Linux系统编程——详解页表
目录 一、前言 二、深入理解页表 三、页表的实际组成 四、总结: 一、前言 页表是我们之前在讲到程序地址空间的时候说到的,它是物理内存到进程程序地址空间的一个桥梁,通过它物理内存的数据和代码才能映射到进程的程序地址空间中ÿ…...

SpringBoot + HttpSession 自定义生成sessionId
SpringBoot HttpSession 自定义生成sessionId 业务场景实现方案 业务场景 最近在做用户登录过程中,由于默认ID是通过UUID创建的,缺乏足够的安全性,决定要自定义生成 sessionId。 实现方案 正常的获取session方法如下: HttpSe…...
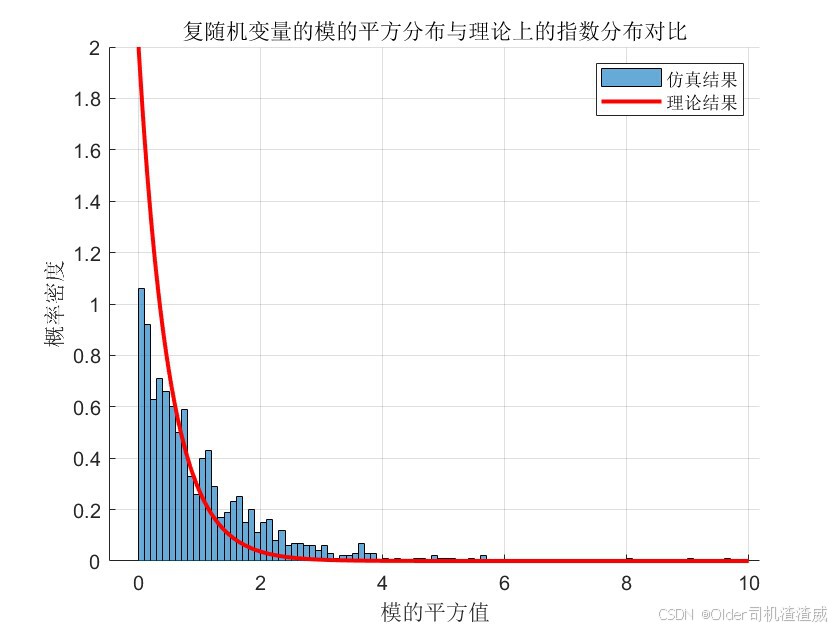
循环对称复高斯分布(Circularly Symmetric Complex Gaussian Distribution)
一、引言 循环对称复高斯分布(Circularly Symmetric Complex Gaussian Distribution,简称CSCG)在无线通信、信号处理等领域具有广泛的应用。作为一种特殊的复高斯分布,CSCG具有独特的性质,如循环对称性、高斯性等&…...
xinput1_3.dll放在哪里?当xinput1_3.dll丢失时的应对策略:详细解决方法汇总
在计算机系统的运行过程中,我们偶尔会遇到一些令人困扰的问题,其中xinput1_3.dll文件丢失就是较为常见的一种情况。这个看似不起眼的动态链接库文件,实则在许多软件和游戏的正常运行中发挥着至关重要的作用。一旦它丢失,可能会导致…...

基于STM32的智能家居环境监控系统设计
目录 引言系统设计 硬件设计软件设计系统功能模块 环境监控模块控制模块显示模块系统实现 硬件实现软件实现系统调试与优化结论与展望 1. 引言 随着智能家居技术的发展,环境监控系统已经成为家居管理的重要组成部分。智能家居环境监控系统通过实时监测室内温度、湿…...

Vscode + gdbserver远程调试开发板指南:
本章目录 步骤环境准备网络配置vscode配置步骤 (全图示例)开发板配置开始调试注意: 每次断开之后,开发板都需要重新启动gdbserver才可调试。 参考链接: 步骤 环境准备 将交叉编译链路径加入$PATH变量:确保系统能够找到所需的工具。 export PATH$PATH:/p…...

大表:适用于结构化数据的分布式存储系统
大家觉得有意义和帮助记得及时关注和点赞!!! 译者序摘要1 引言2 数据模型 2.1 行(Row)2.2 Column Families(列族) 2.2.1 设计2.2.2 column key 的格式:family:qualifier2.2.3 访问控制和磁盘/内存记账(acco…...

深入解析MVCC中Undo Log版本底层存储读取逻辑
一、引言 多版本并发控制(MVCC,Multi-Version Concurrency Control)是一种广泛应用于关系数据库管理系统中的并发控制技术。它通过保存数据的历史版本,使得在事务并发执行时,每个事务都能看到数据的一致性视图。在MVC…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

CVE-2023-25194源码分析与漏洞复现(Kafka JNDI注入)
漏洞概述 漏洞名称:Apache Kafka Connect JNDI注入导致的远程代码执行漏洞 CVE编号:CVE-2023-25194 CVSS评分:8.8 影响版本:Apache Kafka 2.3.0 - 3.3.2 修复版本:≥ 3.4.0 漏洞类型:反序列化导致的远程代…...

break 语句和 continue 语句
break语句和continue语句都具有跳转作用,可以让代码不按既有的顺序执行 break break语句用于跳出代码块或循环 1 2 3 4 5 6 for (var i 0; i < 5; i) { if (i 3){ break; } console.log(i); } continue continue语句用于立即终…...
