正交三角函数全面阐述
目录
1. 正交性定义
2. 正交三角函数
常见的正交三角函数
3. 正交三角函数的特性
4. 正交三角函数在傅里叶分析中的应用
5. 正交三角函数的应用领域
6. 总结
正交三角函数是指在特定条件下,三角函数之间的内积为零。更具体地说,在数学分析、信号处理、傅里叶变换等领域,正交性是非常重要的概念,尤其是在函数空间中的正交基。
1. 正交性定义
两个函数 和
被称为正交的,如果它们在某一特定区间上的内积为零。内积的定义通常是对两个函数进行积分,计算它们的加权平均。对于函数
和
,其内积定义为:
当两个函数 和
满足以下条件时,它们称为正交的:
如果两个函数的内积为零,那么它们在数学上是独立的。正交性是广泛应用于信号分解、傅里叶级数等领域的基础概念。
2. 正交三角函数
在三角函数中,正弦和余弦是常见的正交函数。特别是在傅里叶分析中,正交三角函数用于将复杂的周期信号分解为简单的三角波(正弦波和余弦波)。
常见的正交三角函数
考虑在区间 上定义的正弦函数
和余弦函数
(其中
是整数),这些函数之间满足正交性。具体而言,正弦和余弦函数在特定区间上的内积为零,满足如下正交性条件:
①余弦函数之间的正交性:
(当
时)
另外,满足:
(当
时)
②正弦函数之间的正交性:
(当
时)
同样:
(当
时)
③正弦和余弦函数之间的正交性:
(对于任何
和
)
3. 正交三角函数的特性
-
正交性:正弦函数和余弦函数在不同频率下是正交的。即当我们将这些函数乘在一起并在一定范围内积分时,结果为零。
-
归一性:除了正交性外,这些三角函数在自身的范围内也具有归一性。在区间
上,
和
的积分分别为
,即它们的能量是常数。
-
傅里叶级数:由于正交三角函数的这些特性,傅里叶级数可以将周期函数表示为不同频率的正弦波和余弦波的线性组合。这样,复杂的周期函数可以被分解为一组简单的正交三角函数的加权和。
4. 正交三角函数在傅里叶分析中的应用
傅里叶分析中的一个重要应用是将一个周期信号表示为多个正弦和余弦波的组合。这些正弦和余弦波是正交的,即它们在一定区间上的内积为零,能够独立地表示信号的不同频率成分。
傅里叶级数将周期函数 展开为正弦和余弦的线性组合:
其中:
和
是傅里叶系数,表示信号在相应正弦和余弦基上的投影。
是常数项,表示信号的平均值。
傅里叶级数的核心在于,正弦和余弦函数具有正交性,这使得它们在数学上能够独立地表示信号的不同频率成分,并且可以通过简单的积分计算傅里叶系数。
5. 正交三角函数的应用领域
正交三角函数广泛应用于许多领域,尤其是涉及周期性信号分析的场景:
- 傅里叶分析:用于将周期信号分解为不同频率的正弦波和余弦波。
- 信号处理:在数字信号处理和模拟信号处理中,使用正交三角函数来表示和分析信号。
- 音频和图像压缩:在音频编码(如 MP3)和图像压缩(如 JPEG)中,使用离散傅里叶变换(DFT)和离散余弦变换(DCT)等技术,这些变换基于正交三角函数。
- 振动分析:在机械振动、声学等领域,使用正交三角函数来分析和描述振动模式。
6. 总结
正交三角函数是指正弦和余弦函数在一定区间内的内积为零,且它们具有归一性。它们的正交性使得它们成为表示周期信号的理想基函数。在傅里叶分析中,正弦和余弦函数通过正交性可以将复杂的周期信号分解为不同频率成分,进而对信号进行有效分析和处理。这一特性在信号处理、音频压缩、图像压缩等多个领域都有着广泛的应用。
相关文章:
正交三角函数全面阐述
目录 1. 正交性定义 2. 正交三角函数 常见的正交三角函数 3. 正交三角函数的特性 4. 正交三角函数在傅里叶分析中的应用 5. 正交三角函数的应用领域 6. 总结 正交三角函数是指在特定条件下,三角函数之间的内积为零。更具体地说,在数学分析、信号处…...

《Vue3 四》Vue 的组件化
组件化:将一个页面拆分成一个个小的功能模块,每个功能模块完成自己部分的独立的功能。任何应用都可以被抽象成一棵组件树。 Vue 中的根组件: Vue.createApp() 中传入对象的本质上就是一个组件,称之为根组件(APP 组件…...
)
linux中,mysql数据库分片(分库分表)
1.mysql分库分表:解决单个mysql存储上限问题1.实现方法:存储层面:利用分布式存储解决方案分库分表:拆分库和表到其它服务器2.常用设计思路:垂直分库(库里面的表分开)水平分表(表里面的数据分开)分库:数据库分为多个,每个数据库里面都有表,数据均匀存储分库分表:在分的每库里面,…...

springboot503基于Sringboot+Vue个人驾校预约管理系统(论文+源码)_kaic
摘 要 传统办法管理信息首先需要花费的时间比较多,其次数据出错率比较高,而且对错误的数据进行更改也比较困难,最后,检索数据费事费力。因此,在计算机上安装个人驾校预约管理系统软件来发挥其高效地信息处理的作用&am…...
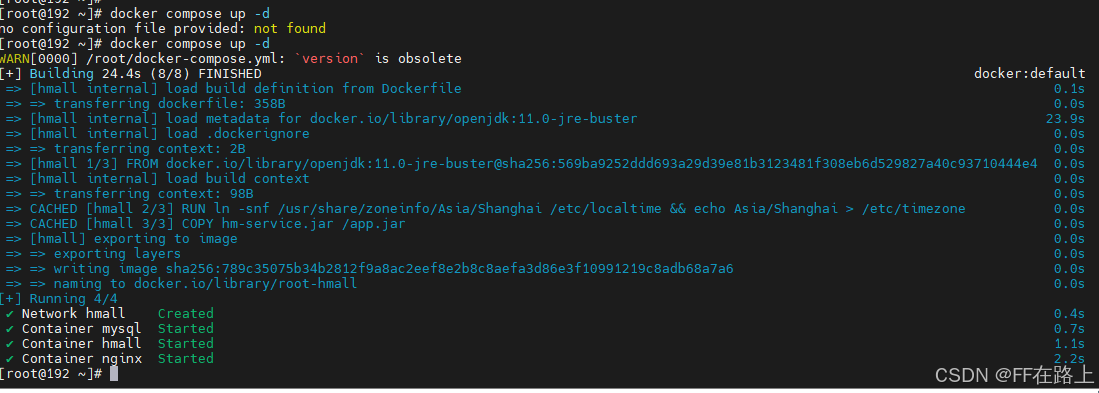
Docker应用-项目部署及DockerCompose
文章目录 Docker应用-项目部署1. 项目部署-后端1.1 修改配置1.2 项目打包1.3 编写Dockerfile1.4 创建镜像1.5 创建并运行容器1.6 测试 2. 项目部署-前端2.1 html前端静态目录2.2 nginx.config编写2.3 部署宿主机服务器2.4 创建容器并挂载2.5 测试 3. DockerCompose3.1 基本语法…...

从0入门自主空中机器人-2-1【无人机硬件框架】
关于本课程: 本次课程是一套面向对自主空中机器人感兴趣的学生、爱好者、相关从业人员的免费课程,包含了从硬件组装、机载电脑环境设置、代码部署、实机实验等全套详细流程,带你从0开始,组装属于自己的自主无人机,并让…...

Kafka高性能设计
高性能设计概述 Kafka高性能是多方面协同的结果,包括集群架构、分布式存储、ISR数据同步及高效利用磁盘和操作系统特性等。主要体现在消息分区、顺序读写、页缓存、零拷贝、消息压缩和分批发送六个方面。 消息分区 存储不受单台服务器限制,能处理更多数据…...

Redis字符串底层结构对数值型的支持常用数据结构和使用场景
字符串底层结构 SDS (Simple Dynamic Strings) 是 Redis 中用于实现字符串类型的一种数据结构。SDS 的设计目标是提供高效、灵活的字符串操作,同时避免传统 C 字符串的一些缺点。 struct sdshdr {int len; // 已使用的长度int free; // 未使用的长度char bu…...

uniapp 微信小程序 数据空白展示组件
效果图 html <template><view class"nodata"><view class""><image class"nodataimg":src"$publicfun.locaAndHttp()?localUrl:$publicfun.httpUrlImg(httUrl)"mode"aspectFit"></image>&l…...

在vscode的ESP-IDF中使用自定义组件
以hello-world为例,演示步骤和注意事项 1、新建ESP-IDF项目 选择模板 从hello-world模板创建 2、打开项目 3、编译结果没错 正在执行任务: /home/azhu/.espressif/python_env/idf5.1_py3.10_env/bin/python /home/azhu/esp/v5.1/esp-idf/tools/idf_size.py /home…...

目标检测,语义分割标注工具--labelimg labelme
1 labelimg labelimg可以用来标注目标检测的数据集, 提供多种格式的输出, 如Pascal Voc, YOLO等。 1.1 安装 pip install labelimg1.2 使用 命令行直接输入labelimg即可打开软件主界面进行操作。 使用非常简单, 不做过细的介绍࿰…...

发明专利与实用新型专利申请过程及自助与代办方式对比
申请专利(发明专利、实用新型专利、外观设计专利)有两种方式:1、自己直接向国家知识产权局申请。2、通过专利代办处申请。以下是对这两种专利类型(发明专利、实用新型专利)申请过程及两种申请方式的详细介绍和对比,参考…...

Datawhale AI冬令营(第二期)动手学AI Agent task2--学Prompt工程,优化Agent效果
目录 如何写好Prompt? 工具包神器1:Prompt框架——CO-STAR 框架 工具包神器2:Prompt结构优化 工具包神器3:引入案例 案例:构建虚拟女友小冰 1. 按照 CO-STAR框架 梳理目标 2. 撰写Prompt 3. 制作对话生成应用&…...

基于python对网页进行爬虫简单教程
python对网页进行爬虫 基于BeautifulSoup的爬虫—源码 """ 基于BeautifulSoup的爬虫###?一、BeautifulSoup简介1.?Beautiful?Soup提供一些简单的、python式的函数用来处理导航、搜索、修改分析树等功能。它是一个工具箱,通过解析文档为用户提供…...

【JavaEE进阶】@RequestMapping注解
目录 📕前言 🌴项目准备 🌲建立连接 🚩RequestMapping注解 🚩RequestMapping 注解介绍 🎄RequestMapping是GET还是POST请求? 🚩通过Fiddler查看 🚩Postman查看 …...

【WebAR-图像跟踪】在Unity中基于Imagine WebAR实现AR图像识别
写在前面的话 感慨一下, WebXR的发展是真的快,20年的时候,大多都在用AR.js做WebAR。随着WebXR标准发展,现在诸如Threejs、AFrame、Unity等多个平台都支持里WebXR。 本文将介绍在Unity中使用 Image Tracker实现Web端的AR图像识别功…...

向bash shell脚本传参
例子: ~ script % touch parameter.sh ~ script % chmod 755 parameter.sh ~ % vim parameter.shparameter.sh: #!/usr/bin/env bashecho the name of current script is $0echo the first parameter is $1echo the second parameter is $2echo all parameters: $…...

Oracle中listagg与wm_concat函数的区别
Oracle中listagg与wm_concat都可以用于将多行数据合并成一个字符串的两个函数,区别如下: 1、分隔符:listagg支持指定分隔符,wm_concat默认为","不支持指定; 2、排序:listagg支持排序后…...

热更新与资源管理
热更新、资源管理、打包发布是 Unity 游戏开发中关键的技术点。这些功能可以极大地提高项目的灵活性和资源利用效率,尤其是在多平台、长生命周期的游戏项目中。以下从技术概述、知识点分析、实现方法和代码举例逐一进行详细分析。 一、热更新 热更新指在不重新发布…...

Momentum Provably Improves Error Feedback!
以下是您提供的论文摘要的翻译: **摘要** 由于在分布式环境中训练机器学习模型时通信开销较高,现代算法不可避免地依赖于有损通信压缩。然而,如果不加以处理,压缩造成的错误会传播,并可能导致严重的不稳定行为&#…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

StarRocks 全面向量化执行引擎深度解析
StarRocks 全面向量化执行引擎深度解析 StarRocks 的向量化执行引擎是其高性能的核心设计,相比传统行式处理引擎(如MySQL),性能可提升 5-10倍。以下是分层拆解: 1. 向量化 vs 传统行式处理 维度行式处理向量化处理数…...
