当前位置： 首页 > news >正文

ShenNiusModularity项目源码学习（6：访问控制）

news 2026/2/9 0:44:23

  ShenNius.Admin.API项目中的控制器类的函数如果需要访问控制，主要是调用ShenNius.Infrastructure项目下的AuthorityAttribute特性类实现的。AuthorityAttribute继承自ActionFilterAttribute抽象类，后者用于在调用控制器操作函数前后自定义处理逻辑，主要支持以下几种事件。AuthorityAttribute类重写了OnActionExecuting事件处理函数，用于在调用控制器类的函数前进行访问控制检查。
**加粗样式**
  访问控制的整体思路还是先检查是否登录用户，然后再根据当前用户权限判断是否能调用当前控制器的指定函数。具体如下：
  1）根据当前上下文中的User.Identity.IsAuthenticated属性判断是否为登录用户，未登录则不允许访问；
  2）如果是DEBUG模式，且当前用户有管理员权限，则不需要访问控制。通过在上下文的User.Claims查找是否有主键为IsAdmin且值为1的数据。但是从源码来看，MVC模式下调用ShenNius.Admin.Mvc的UserController.Login函数登录时用户声明中有IsAdmin信息，但在前后端分类模式下，调用ShenNius.Admin.API的UserController.SignIn函数登录时暂时没有看到设置IsAdmin声明信息的代码；
  3）从函数输入参数中调用ActionExecutingContext.ActionDescriptor. RouteValues获取要访问的控制器类及函数，再从上下文中获取当前用户标识及权限缓存，依次判断当前用户是否有权限访问，但有特例，如果函数名为GetListPages则直接放过。如果是MVC模式，则在用户登录函数中登录验证通过后，会调用MenuRepository.GetCurrentAuthMenus函数获取当前用户权限并返回前端。但是在前后端分类模式下，暂时没有看到是在什么时候获取并保存的当前用户权限。
在这里插入图片描述

参考文献：
[1]https://gitee.com/shenniu_code_group/shen-nius.-modularity

相关文章：

ShenNiusModularity项目源码学习（6：访问控制）

ShenNius.Admin.API项目中的控制器类的函数如果需要访问控制，主要是调用ShenNius.Infrastructure项目下的AuthorityAttribute特性类实现的。AuthorityAttribute继承自ActionFilterAttribute抽象类，后者用于在调用控制器操作函数前后自定义处理逻辑&#…...

编程日记 2024/12/30 3:55:54

STM32F103RCT6学习之三:串口

1.串口基础 2.串口发送 1）基本配置 注意：实现串口通信功能需在keil中设置打开Use Micro LIB，才能通过串口助手观察到串口信息 2)编辑代码 int main(void) {/* USER CODE BEGIN 1 *//* USER CODE END 1 *//* MCU Configuration-------------…...

编程日记 2024/12/30 3:48:45

js 计算税率错误——如何处理

处理方法 var 税额Number(price_notax)*Number(tax_rate)/100;税额税额.toFixed(2);var 含税单价Number(price_notax)Number(税额);var 非小计Number(price_notax)*Number(common_num);var 含税小计Number(含税单价)*Number(common_num);含税小计含税小计.toFixed(2); 税额税额…...

编程日记 2024/12/30 3:46:43

12. 日常算法

1. 主持人调度&#xff08;一&#xff09; 题目来源 class Solution { public:bool hostschedule(vector<vector<int>>& schedule) {// write code heresort(schedule.begin(), schedule.end());int start -1, end 0;for (auto & nums : schedule){end…...

编程日记 2024/12/30 3:45:41

HarmonyOS Next 实现登录注册页面(ARKTS) 并使用Springboot作为后端提供接口

1. HarmonyOS next ArkTS ArkTS围绕应用开发在 TypeScript &#xff08;简称TS&#xff09;生态基础上做了进一步扩展&#xff0c;继承了TS的所有特性&#xff0c;是TS的超集 ArkTS在TS的基础上扩展了struct和很多的装饰器以达到描述UI和状态管理的目的 以下代码是一个基于…...

编程日记 2024/12/30 3:43:39

咖啡即将“从天而降”，无人机外卖时代来袭

如今&#xff0c;在我国的一些城市&#xff0c;无人机配送咖啡已经从设想变为现实&#xff0c;开启了商业化的初步尝试。 当咖啡遇上无人机&#xff0c;奇妙场景开启 想象一下这样的画面&#xff1a;你在户外的露营地&#xff0c;慵懒地躺在帐篷里&#xff0c;或是在城市公园…...

编程日记 2024/12/30 3:38:34

kettle经验篇：Pentaho Repository 类型资源库卡顿问题

2024年马上就结束了&#xff0c;终于在结束前解决了困扰许久的一个问题&#xff1a;kettle的Pentaho Repository 资源库异常卡顿。所以在此也梳理、记录下2024年的最后一个大问题。 项目场景 工作中一个重要内容是数据中心项目&#xff0c;也就必不可少的要用到ETL技术&#x…...

编程日记 2024/12/30 3:37:33

python opencv的sift特征检测(Scale-Invariant Feature Transform)

sift 官方文档地址&#xff1a;https://docs.opencv.org/4.10.0/da/df5/tutorial_py_sift_intro.html 创建SIFT实例cv2.SIFT.create()特征检测sift.detect描述子sift.compute/sift.detectAndCompute画特征cv2.drawKeypoints 原图 特征点 代码 import cv2first ./12.pngsif…...

编程日记 2024/12/30 3:36:33

若依定时任务

表结构 目录 quartz框架 SysJobServiceImpl实现类 使用切点,在构造器执行的时候执行定时任务的构建(这个类是交给IOC容器的,所以这个时间点就是项目启动的时候)SysJobServiceImpl实现类的init方法创建任务 /*** 创建定时任务*/public static void createScheduleJob(Scheduler …...

编程日记 2024/12/30 3:35:32

k8s-node2 NotReady 节点NotReady如何解决？

从集群中移除 k8s-node2 [rootk8s-master ~]# kubectl delete node k8s-node2 node "k8s-node2" deleted重置 k8s-node2 登录到 k8s-node2 上&#xff0c;使用以下命令重置该节点&#xff0c;使其退出集群并恢复到初始状态&#xff1a; [rootk8s-node2 ~]# sudo k…...

编程日记 2024/12/30 3:34:30

Ubuntu通过mDNS实现局域网local域名和octoprint域名访问

OctoPrint是一个开源的3D打印机控制软件&#xff0c;它提供了一个Web界面&#xff0c;允许用户远程监控和管理3D打印机。通过USB连接到打印机后&#xff0c;用户可以使用任何带有Web浏览器的设备来控制打印作业&#xff0c;包括开始、停止、暂停打印&#xff0c;以及在打印过程…...

编程日记 2024/12/30 3:33:29

短视频矩阵账号管理技术源码搭建详解，支持OEM

一、引言 在短视频矩阵系统中&#xff0c;账号管理是至关重要的一环&#xff0c;它涉及到多平台账号的接入、用户信息的安全存储与高效管理、权限的精准控制以及账号数据的同步与更新等关键功能。一个健壮、灵活且安全的账号管理技术架构&#xff0c;能够为整个短视频矩阵系统的…...

编程日记 2024/12/30 3:30:24

【源码 导入教程 文档 讲解】基于springboot校园新闻管理系统源码和论文

可做计算机毕业设计JAVA、PHP、爬虫、APP、小程序、C#、C、python、数据可视化、大数据、文案 传统信息的管理大部分依赖于管理人员的手工登记与管理&#xff0c;然而&#xff0c;随着近些年信息技术的迅猛发展&#xff0c;让许多比较老套的信息管理模式进行了更新迭代&#xf…...

编程日记 2024/12/30 3:29:23

Spark SQL DML语句

【图书介绍】《Spark SQL大数据分析快速上手》-CSDN博客 《Spark SQL大数据分析快速上手》【摘要 书评 试读】- 京东图书 Spark本地模式安装_spark3.2.2本地模式安装-CSDN博客 DML&#xff08;Data Manipulation Language&#xff0c;数据操作语言&#xff09;操作主要用来对…...

编程日记 2024/12/30 3:25:19

开发微信小程序的过程与心得

起因 作为家长&#xff0c;我近期参与了学校的护学岗工作。在这个过程中&#xff0c;我发现需要使用水印相机来记录护学活动&#xff0c;但市面上大多数水印相机应用都要求开通会员才能使用完整功能。作为一名程序员&#xff0c;我决定利用自己的技术背景&#xff0c;开发一个…...

编程日记 2024/12/30 3:24:17

【1224】数据结构（sizeof/数组的长度定义/读取字符串函数/线性表长度/左值右值/静态变量/指针与引用）

1.对一维整型数组a的正确说明是 #define SIZE 10 (换行) int a[SIZE];说法是否正确&#xff1f; 正确 数组的SIZE可以用宏定义&#xff0c;但不能用变量 2.如有定义&#xff1a;char str[20];&#xff0c;能将从键盘输入的字符串“How are you”保存到 str 数组的语句是&#x…...

编程日记 2024/12/30 3:21:13

Android笔记(四十一)：TabLayout内的tab不滚动问题

背景 假设二级页面是上面图片的布局&#xff0c;当进来时TabLayout和ViewPager2绑定完就马上调setCustomItem&#xff0c;跳转到最后一个tab页面时&#xff0c;会发现tab不滚动&#xff0c;手动滑一下ViewPager2时才会滚动tab到正确的位置 原因分析 调用TabLayoutMediator.at…...

编程日记 2024/12/30 3:20:11

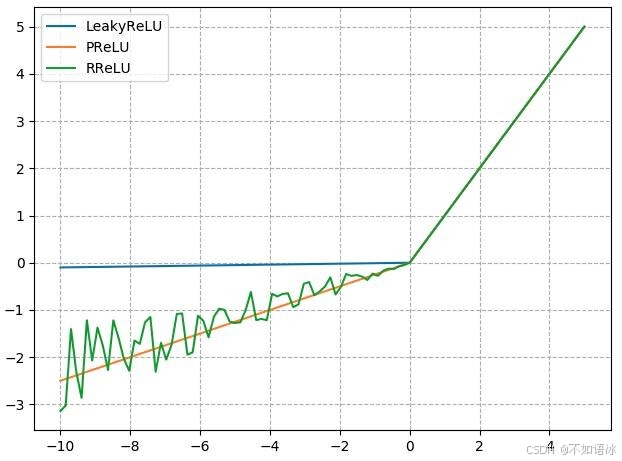
基于pytorch的深度学习基础3——模型创建与nn.Module

三 模型创建与nn.Module 3.1 nn.Module 模型构建两要素&#xff1a; 构建子模块——__init()__拼接子模块——forward&#xff08;&#xff09; 一个module可以有多个module&#xff1b; 一个module相当于一个运算&#xff0c;都必须实现forward函数&#xff1b; 每一个mod…...

编程日记 2024/12/30 3:19:09

Debian-linux运维-docker安装和配置

腾讯云搭建docker官方文档&#xff1a;https://cloud.tencent.com/document/product/213/46000 阿里云安装Docker官方文档&#xff1a;https://help.aliyun.com/zh/ecs/use-cases/install-and-use-docker-on-a-linux-ecs-instance 天翼云常见docker源配置指导&#xff1a;htt…...

编程日记 2024/12/30 3:12:01

Docker完整技术汇总

Docker 背景引入 在实际开发过程中有三个环境&#xff0c;分别是&#xff1a;开发环境、测试环境以及生产环境&#xff0c;假设开发环境中开发人员用的是jdk8&#xff0c;而在测试环境中测试人员用的时jdk7&#xff0c;这就导致程序员开发完系统后将其打成jar包发给测试人员后…...

编程日记 2024/12/30 3:10:57

Linux链表操作全解析

Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表&#xff1f;1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

编程新知 2025/12/3 20:14:32

CTF show Web 红包题第六弹

提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框&#xff0c;很难让人不联想到SQL注入&#xff0c;但提示都说了不是SQL注入&#xff0c;所以就不往这方面想了 ​ 先查看一下网页源码&#xff0c;发现一段JavaScript代码&#xff0c;有一个关键类ctfs…...

编程新知 2026/2/5 4:33:58

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module

1、为什么要修改 CONNECT 报文&#xff1f; 多租户隔离&#xff1a;自动为接入设备追加租户前缀&#xff0c;后端按 ClientID 拆分队列。零代码鉴权&#xff1a;将入站用户名替换为 OAuth Access-Token&#xff0c;后端 Broker 统一校验。灰度发布&#xff1a;根据 IP/地理位写…...

编程新知 2025/8/1 10:20:23

令牌桶 滑动窗口-＞限流 分布式信号量-＞限并发的原理 lua脚本分析介绍

文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结&#xff1a; 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析&#xff1a; 实际业务去理解体会统一注…...

编程新知 2026/1/29 16:36:27

mysql已经安装，但是通过rpm -q 没有找mysql相关的已安装包

文章目录 现象&#xff1a;mysql已经安装&#xff0c;但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时&#xff0c;可能是因为以下几个原因&#xff1a;1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

编程新知 2026/2/4 16:17:25

tree 树组件大数据卡顿问题优化

问题背景 项目中有用到树组件用来做文件目录&#xff0c;但是由于这个树组件的节点越来越多&#xff0c;导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多&#xff0c;导致的浏览器卡顿&#xff0c;这里很明显就需要用到虚拟列表的技术&…...

编程新知 2026/2/8 5:28:24

MySQL账号权限管理指南：安全创建账户与精细授权技巧

在MySQL数据库管理中&#xff0c;合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号&#xff1f; 最小权限原则&#xf…...

编程新知 2025/9/5 23:36:27

rnn判断string中第一次出现a的下标

# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

编程新知 2025/9/24 16:25:00

Python 包管理器 uv 介绍

Python 包管理器 uv 全面介绍 uv 是由 Astral&#xff08;热门工具 Ruff 的开发者&#xff09;推出的下一代高性能 Python 包管理器和构建工具&#xff0c;用 Rust 编写。它旨在解决传统工具&#xff08;如 pip、virtualenv、pip-tools&#xff09;的性能瓶颈&#xff0c;同时…...

编程新知 2026/2/7 10:47:09

基于 TAPD 进行项目管理

起因 自己写了个小工具&#xff0c;仓库用的Github。之前在用markdown进行需求管理&#xff0c;现在随着功能的增加&#xff0c;感觉有点难以管理了&#xff0c;所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD&#xff0c;需要提供一个企业名新建一个项目&#…...

编程新知 2026/1/24 14:15:44