回归问题的等量分层
目录
一、说明
二、什么是分层抽样?
三、那么回归又如何呢?
四、回归分层(Stratification on Regression)

一、说明
在同一个数据集中,我们可以看成是一个抽样体。然而,我们如果将这个抽样体分成两份,每一份依然保留他们的分布(将一个抽样集合合理地分成两个抽样集合),这是我们在训练中经常需要的。在本文中,我将尝试举例说明如何在保留分布比例的情况下对回归问题进行分割。让我们从基础开始。
您可以在 Kaggle 笔记本上查看工作示例:笔记本
二、什么是分层抽样?
分层抽样是从数据集中抽取样本,同时保留两个分组(训练和测试)中类别的比例。例如:
如果我们的数据中有 30% 来自A 类,其余来自B 类;通过分层,我们的训练和测试分割也应该具有相同的比例(例如30%来自A — 70%来自B)。当然,这是一个分类问题的例子,这非常关键,特别是如果我们的数据中存在类别不平衡。如果我们在不使用分层的情况下分割数据,我们可能会得到非常不平衡的分割,这不能正确表示我们模型的泛化能力——或者甚至不给它学习少数类的机会。
三、那么回归又如何呢?
当我们处理分类问题时,我们的数据中有类别标签,我们现在知道如何处理这种数据。但是回归呢?也许我们可以将这个类别比例定义映射到回归问题的分布比例。如果我们将每个值视为一个单独的类别会怎么样?让我们看看。我们将使用来自Kaggle的“房价竞争”数据。
train_df = pd.read_csv("../input/home-data-for-ml-course/train.csv")
labels = train_df["SalePrice"]
print("Unique label count:", labels.nunique())
print("Data length:", len(train_df), "rows")这将产生以下结果:
Unique label count: 663
Data length: 1460 rows如果我们这样做,我们将有663个不同的类别,而我们的数据中只有1460行。这会非常稀疏,我们应该实现一些更聪明的方法。让我们看看标签的分布:
plt.figure(figsize=(12,6))
_ = sns.histplot(data=labels, kde=True, stat="density", bins=30)
我们有一个右偏分布,如果我们随机分割这些数据,似乎对某些折叠来说会有风险。但让我们尝试将其作为基线。
def fold_visualizer(data, fold_idxs, seed_num):fig, axs = plt.subplots(len(fold_idxs)//2, 2, figsize=(15,(len(fold_idxs)//2)*5))fig.suptitle("Seed: " + str(seed_num), fontsize=16)for fold_id, (train_ids, val_ids) in enumerate(fold_idxs):sns.histplot(data=data[train_ids],kde=True,stat="density",alpha=0.15,label="Train Set",bins=30,line_kws={"linewidth":4},ax=axs[fold_id%(len(fold_idxs)//2), fold_id//(len(fold_idxs)//2)])sns.histplot(data=data[val_ids],kde=True,stat="density", color="darkorange",alpha=0.15,label="Validation Set",bins=30,line_kws={"linewidth":4},ax=axs[fold_id%(len(fold_idxs)//2), fold_id//(len(fold_idxs)//2)])axs[fold_id%(len(fold_idxs)//2), fold_id//(len(fold_idxs)//2)].legend()axs[fold_id%(len(fold_idxs)//2), fold_id//(len(fold_idxs)//2)].set_title("Split " + str(fold_id+1))plt.show()让我们使用不同的5个种子创建5 个不同的完全随机 KFold 分割并检查它们:
for i in range(5):baseline_kfold = list(KFold(4,shuffle=True,random_state=i).split(labels))fold_visualizer(data=labels,fold_idxs=baseline_kfold,seed_num=i)




我们可以明确地看到这些分割的分布差异:
- 种子 0 — 分割 3
- 种子 2 — 分组 2
- 种子 4 — 分组 3
它们彼此之间差异很大,这种情况可能会导致我们的模型在这些折叠上表现不稳定。让我们为回归数据实现更广义的分层。
四、回归分层(Stratification on Regression)
正如我们所见,将每个连续值视为单独的类别并不明智。但我们可以使用分箱对它们进行分组。我们可以将标签分成k 个大小相等的区间,并将每个区间定义为一个唯一的类。这里,k是我们应该为我们的问题设置的超参数。
def create_cont_folds(df, n_s=8, n_grp=1000, seed=1):skf = StratifiedKFold(n_splits=n_s, shuffle=True, random_state=seed)grp = pd.qcut(df, n_grp, labels=False)target = grpfold_nums = np.zeros(len(df))for fold_no, (t, v) in enumerate(skf.split(target, target)):fold_nums[v] = fold_nocv_splits = []for i in range(num_of_folds):test_indices = np.argwhere(fold_nums==i).flatten()train_indices = list(set(range(len(labels))) - set(test_indices))cv_splits.append((train_indices, test_indices))return cv_splits我们只需使用pandas库中的.cut()函数即可。它会通过查找数据的最小值和最大值将数据分成相等的间隔。由于我们的分布是偏斜的,我认为使用基于分位数的分箱是有风险的。如果您认为您的分布适合这样做,您可以简单地将.cut()更改为.qcut()。
让我们看看当我们使用分层连续分裂时我们会得到什么:
num_of_folds = 4
num_of_groups = 100for i in range(5):cv_splits = create_cont_folds(labels, n_s=num_of_folds, n_grp=num_of_groups, seed=i)fold_visualizer(data=labels,fold_idxs=cv_splits,seed_num=i)



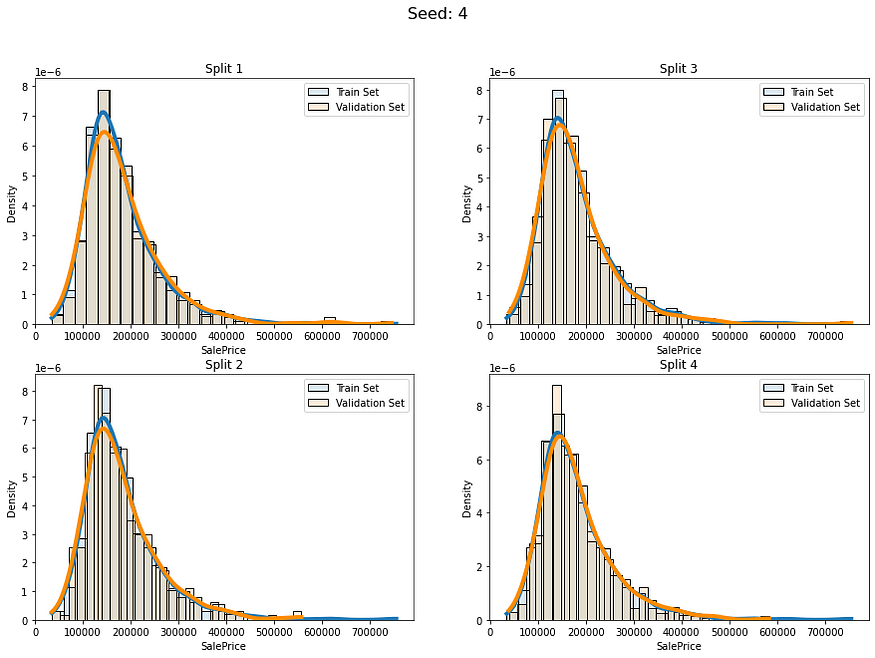
似乎我们避免了以不同的分布比例拆分数据。我们仍然有差异,但我认为这是可以接受的,因为我们的数据只有约1000行。
这就是为回归问题生成分层折叠的全部内容!这确实是一种实现我们想要的结果的简单方法,当然,我们可能会尝试实施不同的方法来实现它。
相关文章:

回归问题的等量分层
目录 一、说明 二、什么是分层抽样? 三、那么回归又如何呢? 四、回归分层(Stratification on Regression) 一、说明 在同一个数据集中,我们可以看成是一个抽样体。然而,我们如果将这个抽样体分成两份&#…...
Unity-Mirror网络框架-从入门到精通之Basic示例
文章目录 前言Basic示例场景元素预制体元素代码逻辑BasicNetManagerPlayer逻辑SyncVars属性Server逻辑Client逻辑 PlayerUI逻辑 最后 前言 在现代游戏开发中,网络功能日益成为提升游戏体验的关键组成部分。Mirror是一个用于Unity的开源网络框架,专为多人…...

CSS 图片廊:网页设计的艺术与技巧
CSS 图片廊:网页设计的艺术与技巧 引言 在网页设计中,图片廊是一个重要的组成部分,它能够以视觉吸引的方式展示图片集合,增强用户的浏览体验。CSS(层叠样式表)作为网页设计的主要语言之一,提供…...

AI 发展的第一驱动力:人才引领变革
在科技蓬勃发展的当下,AI 成为了时代的焦点,然而其发展并非一帆风顺,究竟什么才是推动 AI 持续前行的关键力量呢? 目录 AI 发展现状剖析 期望与现实的落差 落地困境根源 人才:AI 发展的核心动力编辑 技术突破的…...
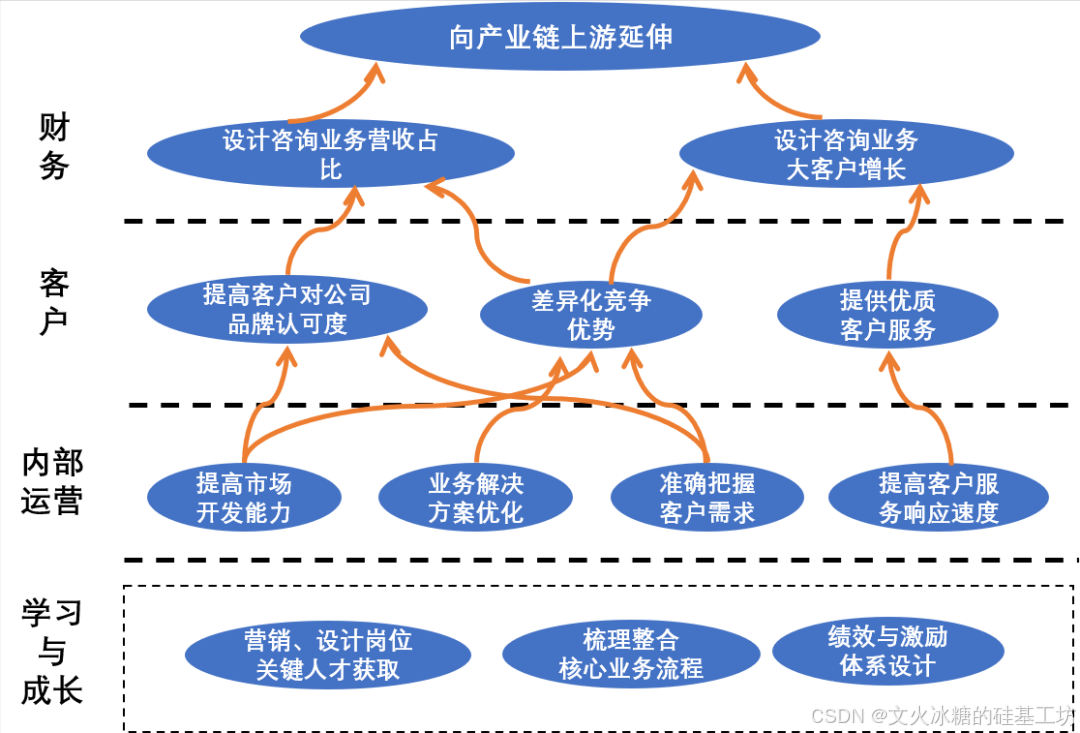
[创业之路-229]:《华为闭环战略管理》-5-平衡记分卡与战略地图
目录 一、平衡记分卡 1. 财务角度: 2. 客户角度: 3. 内部运营角度: 4. 学习与成长角度: 二、BSC战略地图 1、核心内容 2、绘制目的 3、绘制方法 4、注意事项 一、平衡记分卡 平衡记分卡(Balanced Scorecard&…...
用uniapp写一个播放视频首页页面代码
效果如下图所示 首页有导航栏,搜索框,和视频列表, 导航栏如下图 搜索框如下图 视频列表如下图 文件目录 视频首页页面代码如下 <template> <view class"video-home"> <!-- 搜索栏 --> <view class…...

【视觉SLAM:八、后端Ⅰ】
视觉SLAM的后端主要解决状态估计问题,它是优化相机轨迹和地图点的过程,从数学上看属于非线性优化问题。后端的目标是结合传感器数据,通过最优估计获取系统的状态(包括相机位姿和场景结构),在状态估计过程中…...

PaddleOCROCR关键信息抽取训练过程
步骤1:python版本3.8.20 步骤2:下载代码,安装依赖 git clone https://gitee.com/PaddlePaddle/PaddleOCR.git pip uninstall opencv-python -y # 安装PaddleOCR的依赖 ! pip install -r requirements.txt # 安装关键信息抽取任务的依赖 !…...

用Python操作字节流中的Excel文档
Python能够轻松地从字节流中加载文件,在不依赖于外部存储的情况下直接对其进行读取、修改等复杂操作,并最终将更改后的文档保存回字节串中。这种能力不仅极大地提高了数据处理的灵活性,还确保了数据的安全性和完整性,尤其是在网络…...
)
python 桶排序(Bucket Sort)
桶排序(Bucket Sort) 桶排序是一种分布式排序算法,适用于对均匀分布的数据进行排序。它的基本思想是:将数据分到有限数量的桶中,每个桶分别排序,最后将所有桶中的数据合并。 桶排序的步骤: 划…...

Elasticsearch:探索 Elastic 向量数据库的深度应用
Elasticsearch:探索 Elastic 向量数据库的深度应用 一、Elasticsearch 向量数据库简介 1. Elasticsearch 向量数据库的概念 Elasticsearch 本身是一个基于 Lucene 的搜索引擎,提供了全文搜索和分析的功能。随着技术的发展,Elasticsearch 也…...

【每日学点鸿蒙知识】属性变量key、waterflow卡顿问题、包无法上传、Video控件播放视频、Vue类似语法
1、HarmonyOS 属性变量常量是否可以作为object对象的key? a: object new Object() this.a[Constants.TEST_KEY] "456" 可以先定义,再赋值 2、首页点击回到waterflow的首节点,0~index全部节点被重建,导致卡顿 使用s…...

小程序中引入echarts(保姆级教程)
hello hello~ ,这里是 code袁~💖💖 ,欢迎大家点赞🥳🥳关注💥💥收藏🌹🌹🌹 🦁作者简介:一名喜欢分享和记录学习的在校大学生…...
工具——Sequelize介绍与使用,并举案例分析)
基于 Node.js 的 ORM(对象关系映射)工具——Sequelize介绍与使用,并举案例分析
便捷性介绍 支持多种数据库,包括 PostgreSQL、MySQL、MariaDB、SQLite 和 Microsoft SQL Server。Sequelize 提供了丰富的功能,帮助开发者用 JavaScript(或 TypeScript)代码操作数据库,而无需直接书写 SQL 语句。 Se…...
)
python 插入排序(Insertion Sort)
插入排序(Insertion Sort) 插入排序是一种简单的排序算法。它的基本思想是:将数组分为已排序部分和未排序部分,然后逐个将未排序部分的元素插入到已排序部分的正确位置。插入排序类似于整理扑克牌的过程。 插入排序的步骤&#…...

电子应用设计方案81:智能AI冲奶瓶系统设计
智能 AI 冲奶瓶系统设计 一、引言 智能 AI 冲奶瓶系统旨在为父母或照顾者提供便捷、准确和卫生的冲奶服务,特别是在夜间或忙碌时,减轻负担并确保婴儿获得适宜的营养。 二、系统概述 1. 系统目标 - 精确调配奶粉和水的比例,满足不同年龄段婴…...

JAVA高并发总结
JAVA高并发编程总结 在现代应用中,高并发编程是非常重要的一部分,尤其是在分布式系统、微服务架构、实时数据处理等领域。Java 提供了丰富的并发工具和技术,帮助开发者在多线程和高并发的场景下提高应用的性能和稳定性。以下是 Java 高并发编…...

【AIGC】使用Java实现Azure语音服务批量转录功能:完整指南
文章目录 引言技术背景环境准备详细实现1. 基础架构设计2. 实现文件上传功能3. 提交转录任务crul4. 获取转录结果 使用示例结果示例最佳实践与注意事项总结 引言 在当今数字化时代,将音频内容转换为文本的需求越来越普遍。无论是会议记录、视频字幕生成,…...

arcgis模版空库怎么用(一)
这里以某个项目的数据为例: 可以看到,属性表中全部只有列标题,无数据内容 可能有些人会认为空库是用来往里面加入信息的,其实不是,正确的用法如下: 一、下图是我演示用的数据,我们可以看到其中…...

【电机控制】基于STC8H1K28的六步换向——方波驱动(软件篇)
【电机控制】基于STC8H1K28的六步换向——方波驱动(软件篇) 文章目录 [TOC](文章目录) 前言一、main.c二、GPIO.c三、PWMA.c四、ADC.c五、CMP.c六、Timer.c七、PMSM.c八、参考资料总结 前言 【电机控制】STC8H无感方波驱动—反电动势过零检测六步换向法 …...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...
