Statistic for ML
statistical concept 統計學概念
免費完整內容
PMF and CDF
PMF定義的值是P(X=x),而CDF定義的值是P(X <= x),x為所有的實數線上的點。
probability mass function (PMF) 概率質量函數
p X ( x ) = P ( X = x ) pX(x)=P(X=x) pX(x)=P(X=x)
是離散隨機變數在各個特定取值上的概率。有時也被稱為離散密度函數。
概率密度函數通常是定義離散隨機分佈的主要方法,
並且此類函數存在於其定義域是:
- 離散的純量變數
- 多遠隨機變數
維基百科
Cumulative distribution function(CDF)累積分佈函數
F X ( x ) = P ( X < = x ) FX(x)=P(X<=x) FX(x)=P(X<=x)
也叫概率分佈函數或分佈函數
是概率密度函數的積分
能夠完整的描述一個實隨機變數X的概率分佈
維基百科
probability density function(PDF)概率密度函數
概率密度函數(Probability Density Function, PDF)-CSDN博客
Central Limits 中央界限
Support we have a set of independent random variables X i X_{i} Xi for i = 1 , . . . . , n i=1,....,n i=1,....,n with:
M e a n ( X i ) = μ Mean(X_{i})=\mu Mean(Xi)=μ V a r ( X i ) = V Var(X_{i})=V Var(Xi)=V for all i i i
Then as n n n becomes large, the sum:
S m = ∑ i = 1 n X i → N ( n μ , n V ) S_{m}=\sum\limits_{i = 1}^n {{X_i} \to {\rm N}(n\mu ,nV)} Sm=i=1∑nXi→N(nμ,nV)
tends to become normally distributed.
Absence of Central Limits
Another case is where the moments are not defined / infinite 另一種情況是力矩不確定或無限大
Randomness 隨機性
Motivation 動機
Three main ways that random comes into data science:
- The data themselves are often best understood as random 數據本身通常最好被理解為隨機
- **When we want to reason under **subjective uncertainty **(for example in Bayesian approaches) then unknown quantities can be represented as random. Often when we make predictions they will be **probabilitic 當我們主管不確定性的情況下進行推理時,可以將未知量表示為隨機量,當我們進行預測時,他們將是概率性的
- Many of the most effective / efficient / commonly‑used algorithms in data science—typically called Monte Carlo algorithms—exploit randomness. 蒙特卡洛算法
- Unpredictable 不可預測性
- Subjective uncertainty 主管不確定性
The logistic map 邏輯地圖(單峰映象)
是一個二次多項式映射(遞歸關係)经常作为典型范例来说明复杂的混沌现象是如何从非常简单的非线性动力学方程中产生的。
is an example of deterministic chaos 是確定性混沌的一個例子 but whose results are apparently not easy to predict. 結果不容易被預測
它在一定程度上是一个时间离散的人口统计模型
Logistic模型可以描述生物種群的演化,它可以表示成一維非線性迭代方程 x n + 1 = r x n ( 1 − x n ) x_{n+1}=rx_{n}(1-x_{n}) xn+1=rxn(1−xn)
Math:
x ( t + 1 ) = μ x ( t ) ( 1 − x ( t ) ) \displaystyle{ x(t+1)=\mu x(t)(1-x(t)) } x(t+1)=μx(t)(1−x(t))
其中,t为迭代时间步,对于任意的t,x(t)∈[0,1],μ为一可调参数,为了保证映射得到的x(t)始终位于[0,1]内,则μ∈[0,4]。x(t)为在t时刻种群占最大可能种群规模的比例(即现有人口数与最大可能人口数的比率)。当变化不同的参数μ时,该方程会展现出不同的动力学极限行为(即当t趋于无穷大,x(t)的变化情况),包括:稳定点(即最终x(t)始终为同一个数值)、周期(x(t)会在2个或者多个数值之间跳跃)、以及混沌(x(t)的终态不会重复,而会等概率地取遍某区间)。
当μ超过[1,4]时,就会发生混沌现象。该非线性差分方程意在观察两种情形:
• 当人口规模很小时,人口将以与当前人口成比例的速度增长进行繁殖。
• 饥饿(与密度有关的死亡率) ,其增长率将以与环境的”承受能力”减去当前人口所得值成正比的速度下降
然而,Logistic映射作为一种人口统计模型,存在着一些初始条件和参数值(如μ >4)为某值时所导致的混沌问题。这个问题在较老的瑞克模型中没有出现,该模型也展示了混沌动力学。
0 < = μ < = 1 0<=μ<=1 0<=μ<=1:
entropy 熵
另一种方法是利用计算机外部因素来产生随机性, 例如鼠标点击的位置和时间。 在此, 我们将考虑把代码运行的时间作为外部因素
即使用系统时钟当前时间的小数点后六位数字(分辨率为微秒)
R和Matlab 使用軟件包提供隨機數生成的函數
Estimation of π π π using Monte Carlo methods
假設我們將 π \pi π 定義為半徑為1的圓的面積根據其定義來估算這個數字,
we will pick random values of x x x and y y y independently from a uniform distribution between 0 and 1, then let the random variable Z Z Z equal 1 if the point ( x , y ) (x, y) (x,y) falls within the quarter-circle shown and 0 otherwise. This Z Z Z allows us to make an estimate of π π π in that its expected value, E [ Z ] = π / 4 E[Z] = π/4 E[Z]=π/4. We can then define a random variable An to be the average of n n n independent samples of Z Z Z. Formally:
A n = 1 n ∑ i = 1 n Z i = π 4 + ε n {{\rm{A}}_n} = \frac{1}{n}\sum\limits_{i = 1}^n {{Z_i} = \frac{\pi }{4} + {\varepsilon _n}} An=n1i=1∑nZi=4π+εn
Code operation
To deal with this, we’ll repeat the experiment m m m times and make a list of all the estimates
we get. We’ll then arrange these results in ascending order and throw away a certain fraction α \alpha α of the largest and smallest results. The remaining values should provide decent upper and lower bounds for an interval containing π \pi π.
m = 100 # Number of estimates taken
n = 80000 # Number of points used in each estimate
If we increase n n n above, we should get a more accurate estimates of π \pi π each tme we run the experiment, while if we increase m m m, we’ll get more accurate estimates of the endpoints of an interval containing π \pi π.
#Generate a set of m estimates of the area of a unit-radius quarter-circle
np.random.seed(42) # Seed the random number generator
A = np.zeros(m) # A will hold our m estimates
for i in range(0,m):for j in range(0,n):# Generate an (x, y) pair in the unit squarex = np.random.rand()y = np.random.rand()# Decide whether the point lies in or on# the unit circle and set Z accordinglyr = x**2 + y**2if ( r <= 1.0):Z = 1.0else:Z = 0# Add up the contribution to the current estimateA[i] = A[i] + Z# Convert the sum we've built to an estimate of piA[i] = 4.0 * A[i] / float( n )
# Calculate approximate 95% confidence interval for pi based on our Monte Carlo estimates
pi_estimates = np.sort(A)
piLower = np.percentile(pi_estimates,2.5)
piUpper = np.percentile(pi_estimates,97.5)
print(f'We estimate that pi lies between {piLower:.3f} and {piUpper:.3f}.')
standard distribution
Bernoulli 伯努利分佈
P ( X = x ) = p x ( 1 − p ) 1 − x , x = 0 , 1 ; 0 < p < 1 P(X=x) = p^{x}(1-p)^{1-x}, x = 0, 1; 0 < p < 1 P(X=x)=px(1−p)1−x,x=0,1;0<p<1
only have two choices(binary situations). 只有兩個結果 例如成功失敗 硬幣正反面
Random Variable (X): In the context of Bernoulli Distribution, X represents the variable that can take the values 1 or 0, denoting the number of successes occurring.
Bernoulli Trial: An individual experiment or trial with only two possible outcomes.
Bernoulli Parameter: This refers to the probability of success § in a Bernoulli Distribution.
Mean:
E [ X ] = μ = p E[X] = μ = p E[X]=μ=p
Variance:
V a r [ X ] = E [ X 2 ] − ( E [ X ] ) 2 = σ 2 = p ( 1 − p ) o r p q Var[X] = E[X^{2}] - (E[X])^2 \\ =σ2 = p(1 - p) \ or\ pq Var[X]=E[X2]−(E[X])2=σ2=p(1−p) or pq
Applications of Bernoulli Distribution in Business Statistics
1. Quality Control: In manufacturing, every product undergoes quality checks. Bernoulli Distribution helps assess whether a product passes (success) or fails (failure) the quality standards. By analysing the probability of success, manufacturers can evaluate the overall quality of their production process and make improvements.
2. Market Research: Bernoulli Distribution is useful in surveys and market research when dealing with yes/no questions. For instance, when surveying customer satisfaction, responses are often categorised as satisfied (success) or dissatisfied (failure). Analysing these binary outcomes using Bernoulli Distribution helps companies gauge customer sentiment.
3. Risk Assessment: In the context of risk management, the Bernoulli Distribution can be applied to model events with binary outcomes, such as a financial investment succeeding (success) or failing (failure). The probability of success serves as a key parameter for assessing the risk associated with specific investments or decisions.
4. Marketing Campaigns: Businesses use Bernoulli Distribution to measure the effectiveness of marketing campaigns. For instance, in email marketing, success might represent a recipient opening an email, while failure indicates not opening it. Analysing these binary responses helps refine marketing strategies and improve campaign success rates.
Difference between Bernoulli Distribution and Binomial Distribution 伯努利分佈和二項分佈的區分
The Bernoulli Distribution and the Binomial Distribution are both used to model random experiments with binary outcomes, but they differ in how they handle multiple trials or repetitions of these experiments. 同樣是對具有二元結果的隨機實驗進行建模,但在處理多次實驗的方式上有所不同
| Basis | Bernoulli Distribution | Binomial Distribution |
|---|---|---|
| Number of Trials | Single trial | Multiple trials |
| Possible Outcomes | 2 outcomes (1 for success, 0 for failure) | Multiple outcomes (e.g., success or failure) |
| Parameter | Probability of success is p | Probability of success in each trial is p and the number of trials is n |
| Random Variable | X can only be 0 or 1 | X can be any non-negative integer (0, 1, 2, 3, …) |
| Purpose | Describes single trial events with success/failure. | Models the number of successes in multiple trials. |
| Example | Coin toss (Heads/Tails), Pass/Fail, Yes/No, etc. | Counting the number of successful free throws in a series of attempts, number of defective items in a batch, etc. |
Arithmetic with normally-distributed variables
Suppose we have two random variables, X1 and X2 that are independent and are both normally distributed with means µ1 and µ2 **and variances σ12 and σ2 2, respectively.
W = X 1 + X 2 W=X_{1}+X_{2} W=X1+X2
will also be normally distributed
mean:
μ W = μ 1 + μ 2 {\mu_{W}}={\mu_{1}} + {\mu_{2}} μW=μ1+μ2
variance:
σ W 2 = σ 1 2 + σ 2 2 {\sigma^{2}_{W}}={\sigma^{2}_{1}}+{\sigma^{2}_{2}} σW2=σ12+σ22
Y = a X 1 + b Y=aX_{1}+b Y=aX1+b
will also be normally distributed
mean:
μ Y = a μ 1 + b \mu_{Y}=a\mu_{1}+b μY=aμ1+b
variance:
σ Y 2 = a 2 σ 1 2 \sigma^{2}_{Y}=a^{2}\sigma^{2}_{1} σY2=a2σ12
CDF
Cauchy 柯西分佈
The Cauchy distribution has probability density function
f ( x ) = 1 π s ( 1 + ( ( x − t ) / s ) 2 ) f(x) = \frac{1}{{\pi s(1 + {{((x - t)/s)}^2})}} f(x)=πs(1+((x−t)/s)2)1
s s s is positive t t t is parameter can be any parameters
It has “heavy tails”, which means that large values are so common that the Cauchy distribution lacks a well-defined mean and variance!
But the parameter t t t gives the location of the mode and median, which are well-defined.
The parameter s s s determines the ‘width’ of the distribution as measured using e.g. the distances between percentiles, which are also well defined.
CDF
EDA: Exploratory data analysis
motivation:
EDA is about getting an intuitive understanding of the data, and as such different people will find different techniques useful.
Data quality
The first thing understand is where the data come from and how accurate they are. 數據的來源和準確性
star rating 星級評級
This is based on experience rather than any formal theory:
- 4: Numbers we can believe. Examples: official statistics(官方統計數據); well controlled laboratory experiments
- 3: Numbers that are reasonably accurate. Examples: well conducted surveys / samples; field measurements; less well controlled experiments.
- 2:Numbers that could be out by quite a long way. Examples: poorly conducted surveys / samples; measurements of very noisy systems
- 1: Numbers that are unreliable. Examples: highly biased / unrepresentative surveys / samples; measurements using biased / low-quality equipment
- 0: Numbers that have just been made up. Examples: urban legends / memes; fabricated experimental data
Univariate Data Vectors
univariate case: one measurement per ‘thing’ 每個變量都單獨探索
Mathematically, we represent a univariate dataset as a length-n vector:
x = ( x 1 , x 2 , . . . , x n ) x = (x_{1},x_{2},...,x_{n}) x=(x1,x2,...,xn)
The sample mean of a function f (x) is
⟨ f ( x ) ⟩ = 1 n ∑ i = 1 n f ( x i ) = 1 n [ f ( x 1 ) + f ( x 2 ) + . . . . + f ( x n ) ] \left\langle {{\rm{f}}(x)} \right\rangle = \frac{1}{n}\sum\limits_{i = 1}^n {f({x_i}) = \frac{1}{n}[f({x_1}) + f({x_2}) + .... + f({x_n})]} ⟨f(x)⟩=n1i=1∑nf(xi)=n1[f(x1)+f(x2)+....+f(xn)]
Visualisation and Information
There is an important distinction in visualisations between
- Lossless(無損) ones from which, if viewed at sufficiently high resolution, one could recover the original dataset
- Lossy(有損) ones, where a given plot would be consistent with many different raw datasets
Typically for complex data, choosing the lossy visualistaion that loses the ‘right’ information is key to successful visualisation.
Multivariate Exploratory Data Analysis
- In real applications, we almost almost always have multiple features of different things measured, and are so in a multivariate rather than univariate situation
Professional Skill
Data types
- Nominal or categorical (e.g. colours, car names): not ordered; cannot be added or compared; can be relabelled.
- Ordinal (e.g. small/medium/large): sometimes represented by numbers; can be ordered, but differences or ratios are not meaningful.
- Measurement: meaningful numbers, on which (some) operations make sense. They can be:
- Discrete (e.g. publication year, number of cylinders): typically integer.
- Continuous (e.g. height): precision limited only by measurement accuracy.
Measurements can be in an interval scale (e.g. temperature in degrees Celsius), ratio scale (say, weights in kg), or circular scale (time of day on the 24 hr clock), depending on the 0 value and on which operations yield meaningful results
Summary Statistics
Measures of Central Tendency 集中趨勢測度
Often, we are interested in what a typical value of the data;
- The mean of the data is:
M e a n ( x ) = ⟨ x ⟩ = 1 n ∑ i = 1 n x i Mean(x)=\left\langle {\rm{x}} \right\rangle = \frac{1}{n}\sum\limits_{i = 1}^n {{x_i}} Mean(x)=⟨x⟩=n1i=1∑nxi
- The median of the data is the value that sits in the middle when the data are sorted by value
- A mode in data is a value of x x x that is ‘more common’ than those around it, or a ‘local maximum’ in the density.
- For discrete data[离散数据] this can be uniquely determined as the most common value
- For continuous data, modes need to be estimated, one aspect of a major strand in data science, estimating distributions.
Visualising
For the data, we estimate from the kernel density that there is one mode, and its location and calculate the mean and median directly
Example:
The data are right-skewed(右偏的), and as a consequence of this the mode is smallest and the mean is largest – we will consider this further; (note that for a normal distribution all would be equal.)
Variance
| 特性 | 有偏差方差 | 無偏差方差 |
|---|---|---|
| 分母 | n | n-1 |
| 應用場景 | 描述樣本的離散型 | 估計總體的方差 |
| 偏差 | 對總體方差的估計存在低估偏差 | 對總體方差的估計是無偏的 |
| 應用場景 | 數據分析、機器學習中的樣本優化 | 統計學中總體方差估計 |
何时使用?
- 有偏差方差 :在机器学习中,通常计算样本的有偏差方差(分母为 nnn),因为重点在于优化模型对样本的适配性,而非推断总体。
- 无偏差方差 :在统计学和推断中,需要用无偏差方差(分母为 n−1n-1n−1),因为它更准确地估计总体参数。
V a r ( x ) = ⟨ ( x − ⟨ x ⟩ ) 2 ⟩ = 1 n ∑ i = 1 n ( x i − ⟨ x ⟩ ) 2 = 1 n ∑ i = 1 n ( x 2 i − 2 x i ⟨ x ⟩ + ⟨ x ⟩ 2 ) = ( 1 n ∑ i = 1 n x i 2 ) + 2 ( 1 n ∑ i = 1 n x i ) ⟨ x ⟩ + 1 n ( ∑ i = 1 n 1 ) ⟨ x ⟩ 2 = 1 n ( ∑ i = 1 n x i 2 ) − ( 1 n ∑ i = 1 n x i ) 2 = ⟨ x 2 ⟩ − ⟨ x ⟩ 2 \begin{array}{ccccc} Var(x) = \left\langle {{{(x - \left\langle x \right\rangle )}^2}} \right\rangle\\ = \frac{1}{n}\sum\limits_{i = 1}^n {{{({x_i} - \left\langle x \right\rangle )}^2}}\\ =\frac{1}{n}\sum\limits_{i = 1}^n {({x^2}_i - 2{x_i}\left\langle x \right\rangle + {{\left\langle x \right\rangle }^2})}\\ =\left( {\frac{1}{n}\sum\limits_{i = 1}^n {x_i^2} } \right) + 2\left( {\frac{1}{n}\sum\limits_{i = 1}^n {{x_i}} } \right)\left\langle x \right\rangle + \frac{1}{n}\left( {\sum\limits_{i = 1}^n 1 } \right){\left\langle x \right\rangle ^2}\\ =\frac{1}{n}\left( {\sum\limits_{i = 1}^n {x_i^2} } \right) - {\left( {\frac{1}{n}\sum\limits_{i = 1}^n {{x_i}} } \right)^2}\\ =\left\langle {{x^2}} \right\rangle - {\left\langle x \right\rangle ^2} \end{array} Var(x)=⟨(x−⟨x⟩)2⟩=n1i=1∑n(xi−⟨x⟩)2=n1i=1∑n(x2i−2xi⟨x⟩+⟨x⟩2)=(n1i=1∑nxi2)+2(n1i=1∑nxi)⟨x⟩+n1(i=1∑n1)⟨x⟩2=n1(i=1∑nxi2)−(n1i=1∑nxi)2=⟨x2⟩−⟨x⟩2
Unbiased Variance and Computation 無偏方差
V a r ^ ( x ) = n n − 1 V a r ( x ) = 1 n − 1 ∑ i = 1 n ( x i − ⟨ x ⟩ ) 2 = 1 n − 1 ( ∑ i = 1 n x i 2 − 1 n ( ∑ i = 1 n x i ) 2 ) \begin{array}{ccccc} \widehat {Var}(x) = \frac{n}{{n - 1}}Var(x) \\ = \frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{({x_i} - \left\langle x \right\rangle )}^2}}\\ = \frac{1}{{n - 1}}\left( {\sum\limits_{i = 1}^n {x_i^2 - \frac{1}{n}{{\left( {\sum\limits_{i = 1}^n {{x_i}} } \right)}^2}} } \right) \end{array} Var (x)=n−1nVar(x)=n−11i=1∑n(xi−⟨x⟩)2=n−11(i=1∑nxi2−n1(i=1∑nxi)2)
默認情況下, python計算有偏差的,R計算無偏差的
無偏差樣本
‘Natural’ units
there are two commonly-used quantities that have the same units as the data 與數據有相同單位
- mean μ = M e a n ( x ) \mu = Mean(x) μ=Mean(x)
- standard deviation σ = V a r ( x ) \sigma = \sqrt {Var(x)} σ=Var(x)
These two quantities let us define two transformations commonly applied to data 用於數據轉換
- centring y i = x i − μ {y_i} = {x_i} - \mu yi=xi−μ | M e a n ( y ) = 0 Mean(y) = 0 Mean(y)=0
- standardisation z i = y i σ {z_i} = \frac{{{y_i}}}{\sigma } zi=σyi | V a r ( z ) = 1 Var(z)=1 Var(z)=1
Higher moments
-
In general, the r r r-th moment of the data is 第 r r r時刻的數據是 m r = ⟨ x r ⟩ {m_r} = \left\langle {{x^r}} \right\rangle mr=⟨xr⟩
-
The r r r-th central moment中心距 of the data is μ r = ⟨ ( x − μ ) r ⟩ = ⟨ y r ⟩ {\mu _r} = \left\langle {{{(x - \mu )}^r}} \right\rangle = \left\langle {{y^r}} \right\rangle μr=⟨(x−μ)r⟩=⟨yr⟩
where the y’s are the centred versions of the data.
-
The r r r-th standardised moment of the data is μ r = ⟨ ( x − μ σ ) r ⟩ = ⟨ z r ⟩ = ⟨ ( x − μ ) 2 ⟩ σ r = μ r σ r {\mu _r} = \left\langle {{{(\frac{{x - \mu }}{\sigma })}^r}} \right\rangle = \left\langle {{z^r}} \right\rangle = \frac{{\left\langle {{{\left( {x - \mu } \right)}^2}} \right\rangle }}{{{\sigma ^r}}} = \frac{{{\mu _r}}}{{{\sigma ^r}}} μr=⟨(σx−μ)r⟩=⟨zr⟩=σr⟨(x−μ)2⟩=σrμr
In theory, all higher moments are informative about the data, but in practice those with r = 3 and r = 4 are most commonly reported
standardised moment
M k = μ k σ k = 原始矩 標準差 {M_k} = \frac{{{\mu _k}}}{{{\sigma ^k}}}=\frac{{{原始矩}}}{{{標準差}}} Mk=σkμk=標準差原始矩
- M k M_k Mk:第 k k k阶标准化矩。
- μ k \mu_k μk:第 k k k 阶原始矩。
- σ \sigma σ:标准差
标准化矩通过除以标准差的 k k k 次方,使矩的量纲消失,方便分布的比较
第一阶标准化矩
M 1 = μ 1 σ 1 {M_1} = \frac{{{\mu _1}}}{{{\sigma ^1}}} M1=σ1μ1
表示分布的中心位置,但通常为 0(如果中心点选均值)
第二阶标准化矩
M 2 = μ 2 σ 2 {M_2} = \frac{{{\mu _2}}}{{{\sigma ^2}}} M2=σ2μ2
恒等于 1,因为分布已经用标准差标准化。
第三阶标准化矩(偏度,Skewness)
M 3 = μ 3 σ 3 = μ 3 ~ = S k e w ( x ) {M_3} = \frac{{{\mu _3}}}{{{\sigma ^3}}}=\widetilde {{\mu _3}} = Skew(x) M3=σ3μ3=μ3 =Skew(x)
-
用于描述分布的对称性或偏斜程度
- M 3 > 0 {{\rm{M}}_3} > 0 M3>0: 分佈 偏右(右尾較長)
- M 3 < 0 {{\rm{M}}_3} < 0 M3<0: 分佈偏左(左尾較長)
- M 3 = 0 {{\rm{M}}_3} = 0 M3=0: 分佈對稱
-
A larger (more positive) value of this quantity indicates right-skewness, meaning that more of the data’s variability arises from values of x larger than the mean
-
Conversely, a smaller (more negative) value of this quantity indicates left-skewness, meaning that more of the data’s variability arises from values of x smaller than the mean.
-
A value close to zero means that the variability of the data is similar either side of the mean (but does not imply an overall symmetric distribution).
第四阶标准化矩(峰度,Kurtosis)
M 4 = μ 4 σ 4 {M_4} = \frac{{{\mu _4}}}{{{\sigma ^4}}} M4=σ4μ4
- 用于描述分布的尖峰或平坦程度.
- M 4 > 3 {{\rm{M}}_4} > 3 M4>3: 尖峰分佈
- M 4 < 3 {{\rm{M}}_4} < 3 M4<3: 平坦分佈
用途
- 描述分布形状 :偏度和峰度是最常用的标准化矩,用于研究数据分布的对称性和尾部特性。
- 模型假设检验 :例如,判断数据是否符合正态分布。
- 分布比较 :通过标准化,消除了尺度和单位的影响,可以直接比较不同数据集的形状特征。
- A value of this quantity larger than 3 means that more of the variance of the data arises from the tails than would be expected if it were normally distributed
- A value of this quantity less than 3 means that less of the variance of the data arises from the tails than would be expected if it were normally distributed.
- A value close to 3 is consistent with, though not strong evidence for, a normal distribution.
- The difference between the kurtosis and 3 is called the excess kurtosis.
functions
Quantiles and Order Statistics
- The z-th percentile, P z P_z Pz is the value of x for which z% of the data is ≤ x
- So the median is median(x) = P 50 P_{50} P50
- This is related to the ECDF as illustrated below
- A measure of dispersal of the data is the inter-quartile range I Q R ( x ) = P 75 − P 25 IQR(x) = {P_{75}} - {P_{25}} IQR(x)=P75−P25
Density Estimation
Histograms
histogram can be used to make an estimate of the probability density underlying a data set. Given data{ x 1 , . . . , x n { {x_1}, . . . , {x_n} } x1,...,xn} and a collection of q + 1 bin-boundaries, b = ( b 0 , b 1 , . . . , b q ) b = (b_0, b_1, . . . , b_q ) b=(b0,b1,...,bq)
chosen so that b 0 < m i n ( x ) a n d m a x ( x ) < b q {b_0} < min(x) \ and \ max(x) < {b_q} b0<min(x) and max(x)<bq , we can think of the histogram-based density estimate as a piecewise-constant (that is, constant on intervals) function arranged so that the value of the estimator in the interval b a − 1 ≤ x < b a b_{a−1} ≤ x < b_{a} ba−1≤x<ba is
f ( x ∣ b ) = 1 b a − b a − 1 ( ∣ { x j ∣ b a − 1 ≤ x j < b a } ∣ n ) f(x|b) = \frac{1}{{{b_a} - {b_{a - 1}}}}\left( {\frac{{\left| {\{ {x_j}|{b_{a - 1}} \le {x_j} < {b_a}\} } \right|}}{n}} \right) f(x∣b)=ba−ba−11(n∣{xj∣ba−1≤xj<ba}∣)
where the second factor is the proportion of the x j {x_j} xj that fall into the interval and b a − b a − 1 b_a − b_{a−1} ba−ba−1 is the width of the interval. These choices mean that the bar (of the histogram) above the interval has an area equal to the proportion of the data points x j x_j xj that fall in that interval
Estimating a Density with Kernels
f ^ ( x ∣ w ) = 1 n ∑ j = 1 n 1 w K ( x − x j w ) \widehat f(x|w) = \frac{1}{n}\sum\limits_{j = 1}^n {\frac{1}{w}K\left( {\frac{{x - {x_j}}}{w}} \right)} f (x∣w)=n1j=1∑nw1K(wx−xj)
The main players in this formula are
K ( x ) K(x) K(x): the kernel, typically some bump-shaped function such as a Gaussian or a parabolic bump. It should be normalised in the sense that
∫ − ∞ ∞ K ( x ) d x = 1 \int_{ - \infty }^\infty {K(x)\ dx = 1} ∫−∞∞K(x) dx=1
w w w : the bandwidth, which sets the width of the bumps
Kernel Density Estimation (KDE)
是一种 非参数方法 ,用于估计随机变量的概率密度函数(PDF,Probability Density Function)。它提供了一种平滑方式来描述数据的分布,不依赖特定的分布假设(如正态分布)
目标 :
- KDE 的目标是从有限的样本数据中估计其背后的概率密度函数。
- 与直方图类似,KDE 描述了数据的分布,但比直方图更平滑且不受特定区间(bin)的影响。
核心公式 :
给定 n n n 个数据点 { x 1 , x 2 , … , x n } \{x_1, x_2, \dots, x_n\} {x1,x2,…,xn},KDE 在位置 x x x 处的估计值为:
f ( x ) = 1 n h ∑ i = 1 n K ( x − x i h ) f ^ ( x ) = 1 n h ∑ i = 1 n K ( x − x i h ) :在 x 处的密度估计。 f^(x)=1nh∑i=1nK(x−xih)\hat{f}(x) = \frac{1}{n h} \sum_{i=1}^{n} K\left(\frac{x - x_i}{h}\right):在 x 处的密度估计。 f(x)=1nh∑i=1nK(x−xih)f^(x)=nh1i=1∑nK(hx−xi):在x处的密度估计。
- K ( ⋅ ) K(\cdot) K(⋅): 核函数 (Kernel Function),定义如何分布平滑权重。
- h h h: 带宽参数 (Bandwidth),控制平滑的程度。
- x i x_i xi:数据点。
核函数 K ( ⋅ ) K(\cdot) K(⋅) :
- 核函数是一个对称的非负函数,其积分为 1,通常用来为每个点分配权重。
- 常见核函数:
- 高斯核(Gaussian Kernel): K ( u ) = 12 π e − u 22 K ( u ) = 1 2 π e − u 2 2 K(u)=12πe−u22K(u) = \frac{1}{\sqrt{2\pi}} e^{-\frac{u^2}{2}} K(u)=12πe−u22K(u)=2π1e−2u2
- 均匀核(Uniform Kernel): K ( u ) = 12 K ( u ) = 1 2 K(u)=12K(u) = \frac{1}{2} K(u)=12K(u)=21(如果 ∣ u ∣ ≤ 1 ∣ u ∣ ≤ 1 ∣u∣≤1|u| \leq 1 ∣u∣≤1∣u∣≤1,否则为 0)
- 三角核(Triangular Kernel): K ( u ) = 1 − ∣ u ∣ K ( u ) = 1 − ∣ u ∣ K(u)=1−∣u∣K(u) = 1 - |u| K(u)=1−∣u∣K(u)=1−∣u∣(如果 ∣ u ∣ ≤ 1 ∣ u ∣ ≤ 1 ∣u∣≤1|u| \leq 1 ∣u∣≤1∣u∣≤1,否则为 0)
带宽 h h h:
-
带宽控制了核的扩展范围。
-
h h h 的选择非常重要:
- h h h 太小:估计函数会过于波动(过拟合)。
- h h h 太大:估计函数会过于平滑(欠拟合)。
-
KDE 的核心思想是用核函数 K ( ⋅ ) K(\cdot) K(⋅)平滑地“覆盖”每个数据点。
-
通过将核函数中心放在每个数据点上,并根据带宽 h h h 调整宽度,最终生成一个连续的概率密度曲线
KDE与直方图的比较
| 特點 | 直方圖 | KDE |
|---|---|---|
| 區間 | 数据被划分成固定宽度的区间(bin) | 不需要固定区间 |
| 平滑性 | 曲线可能不连续,有棱角 | 曲线连续、平滑 |
| 參數 | 区间宽度(bin width) | 核函数和带宽(kernel + bandwidth) |
| 靈活性 | 对区间位置敏感 | 更灵活,适用于复杂数据分布 |
应用场景
- 数据分布可视化 :如观察数据的集中趋势和分布形态。
- 异常检测 :识别不符合密度分布的数据点。
- 概率密度估计 :用于机器学习和统计建模中的特征分布建模。
相关文章:

Statistic for ML
statistical concept 統計學概念 免費完整內容 PMF and CDF PMF定義的值是P(Xx),而CDF定義的值是P(X < x),x為所有的實數線上的點。 probability mass function (PMF) 概率質量函數 p X ( x ) P ( X x ) pX(x)P(Xx) pX(x)P(Xx) 是離散隨機變數…...

Django 中数据库迁移命令
在 Django 中,python manage.py makemigrations、python manage.py sqlmigrate polls 0003 和 python manage.py migrate 是与数据库迁移相关的重要命令。它们的作用和对应内容如下: 1. python manage.py makemigrations 功能: 此命令会根据你的模型文…...
)
【机器学习】 卷积神经网络 (CNN)
文章目录 1. 为什么需要 CNN2. CNN 的架构3. 卷积层4. 池化层5. CNN 的应用 1. 为什么需要 CNN 前提:利用前置知识,去掉全连接神经网络中的部分参数,提升学习效率。本质:在 DNN 之前加上 CNN,先去除不必要的参数&…...

Linux中操作中的无痕命令history技巧
当我们需要查看Linux下的操作记录时,就可以用history命令来查看历史记录 1、关闭history记录功能,如果不想让别人看到自己在Linux上的操作命令,可以用这个命令 set o history 2、打开history记录功能 set -o history3、清空记录 histor…...

在CE自动汇编里调用lua函数
CE自动汇编模板里有一个是调用lua函数,但是关于如何使用的资料很少,结果问AI也是各种错误回答,还各种误导... 下面是32位游戏的例子: loadlibrary(luaclient-i386.dll) luacall(openLuaServer(CELUASERVER))CELUA_ServerName: d…...
如何在没有 iCloud 的情况下将联系人从 iPhone 传输到 iPhone
概括 近期iOS 13.5的更新以及苹果公司发布的iPhone SE在众多iOS用户中引起了不小的轰动。此外,不少变化,如暴露通知 API、Face ID 增强功能以及其他在 COVID-19 期间与公共卫生相关的新功能,吸引了 iPhone 用户尝试新 iPhone 并更新到最…...

欧科云链研究院:ChatGPT 眼中的 Web3
编辑|OKG Research 转眼间,2024年已经进入尾声,Web3 行业经历了热闹非凡的一年。今年注定也是属于AI的重要一年,OKG Research 决定拉上 ChatGPT 这位“最懂归纳的AI拍档”,尝试把一整年的研究内容浓缩成精华。我们一共…...

行为模式2.命令模式------灯的开关
行为型模式 模板方法模式(Template Method Pattern)命令模式(Command Pattern)迭代器模式(Iterator Pattern)观察者模式(Observer Pattern)中介者模式(Mediator Pattern…...

Kerberos用户认证-数据安全-简单了解-230403
hadoop安全模式官方文档:https://hadoop.apache.org/docs/r2.7.2/hadoop-project-dist/hadoop-common/SecureMode.html kerberos是什么 kerberos是计算机网络认证协议,用来在非安全网络中,对个人通信以安全的手段进行身份认证。 概念&#…...

【Multisim用74ls92和90做六十进制】2022-6-12
缘由Multisim如何用74ls92和90做六十进制-其他-CSDN问答 74LS92、74LS90参考...

滴滴工作流引擎Turbo与logicFlow研究
目录 logicFlow turbo 工作流引擎很多,也都提供了前端UI库,但是太过于冗杂了,元数据表都几十个,logincFlow和Turbo的组合提供了轻量化方式,turbo后端代码只有5个元数据表,logicFlow也提供了bpm的相关扩展功能,但缺点是turbo社区不活跃,logicFlow个人认为跟echarts这种…...

AE Pinnacle 10x6 kW DeviceNet MDXL User r Manual
AE Pinnacle 10x6 kW DeviceNet MDXL User r Manual...

Flutter Android修改应用名称、应用图片、应用启动画面
修改应用名称 打开Android Studio,打开对应项目的android文件。 选择app下面的manifests->AndroidManifest.xml文件,将android:label"bluetoothdemo2"中的bluetoothdemo2改成自己想要的名称。重新启动或者重新打包,应用的名称…...
)
Nginx rewrite 执行顺序(草稿,下次继续编辑)
个人结论: 1.server层ngx_http_rewrite_module模块相关指令按照配置顺序依次执行; 2.server层执行完break指令后,该层级所有跟ngx_http_rewrite_module模块相关的指令都不再被执行,但是不影响其他模块(例如:https://zhuanlan.zhihu.com/p/357…...

01.03周五F34-Day44打卡
文章目录 1. 这家医院的大夫和护士对病人都很耐心。2. 她正跟一位戴金边眼镜的男士说话。3. 那个人是个圆脸。4. 那个就是传说中的鬼屋。5. 他是个很好共事的人。6. 我需要一杯提神的咖啡。7. 把那个卷尺递给我一下。 ( “卷尺” 很复杂吗?)8. 他收到了她将乘飞机来的消息。9.…...

数字货币支付系统开发搭建:构建未来的区块链支付生态
随着数字货币的迅猛发展,越来越多的企业和机构开始关注如何搭建一个高效、安全、可扩展的数字货币支付系统。区块链技术因其去中心化、安全性高、透明性强等优势,已成为开发数字货币支付系统的首选技术。本文将深入探讨数字货币支付系统的开发和搭建过程…...

NLP CH3复习
CH3 3.1 几种损失函数 3.2 激活函数性质 3.3 哪几种激活函数会发生梯度消失 3.4 为什么会梯度消失 3.5 如何解决梯度消失和过拟合 3.6 梯度下降的区别 3.6.1 梯度下降(GD) 全批量:在每次迭代中使用全部数据来计算损失函数的梯度。计算成本…...

BurpSuite2024.11
新增功能 2024 年 11 月 25 日,版本 24.11 此版本引入了站点地图过滤器 Bambdas、匹配和替换 Bambdas、用于 API 扫描的动态身份验证令牌,以及用于入侵者攻击的增强负载管理。我们还进行了多项用户体验改进、性能改进和一些错误修复。 使用 Bambdas 过…...
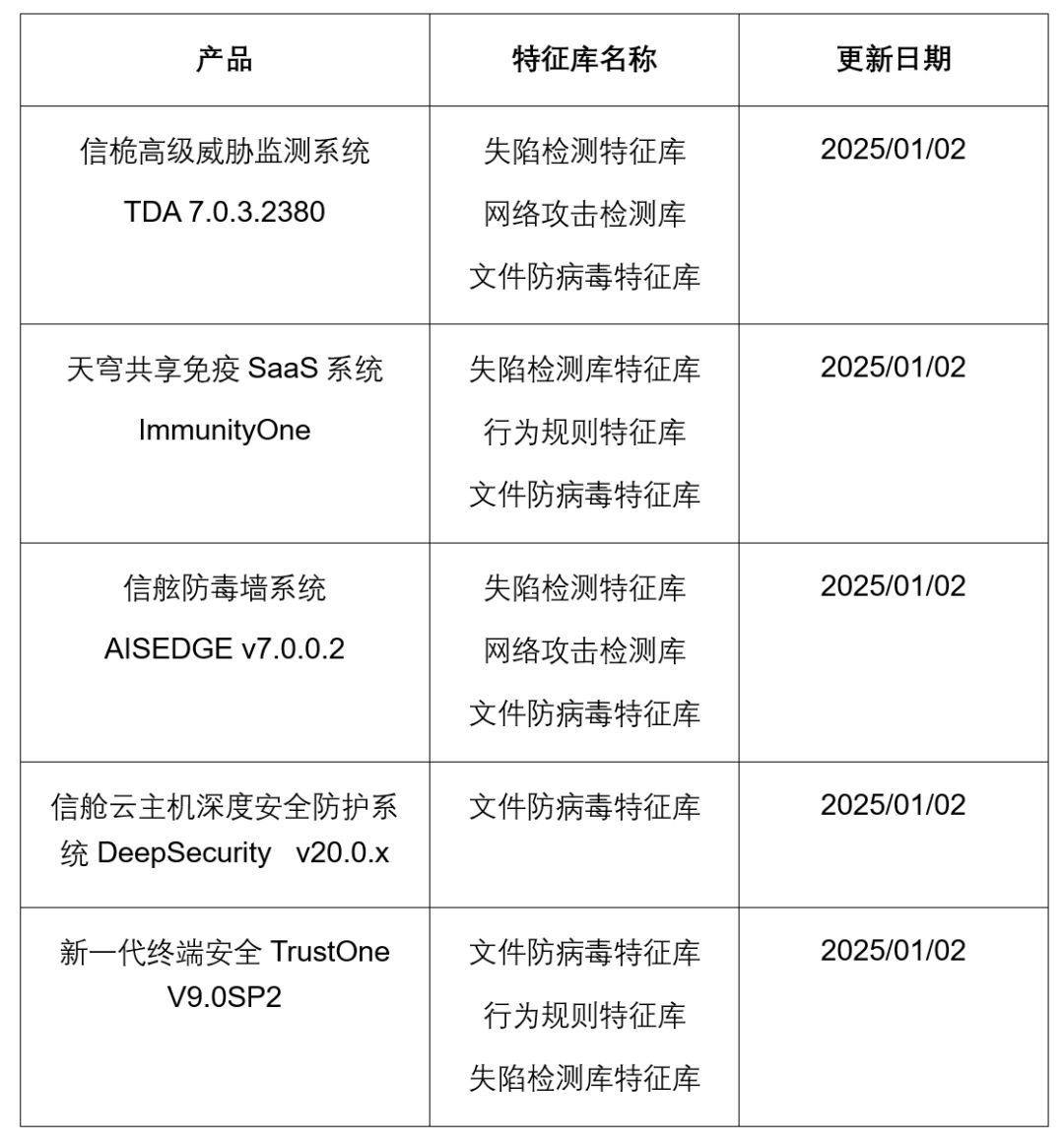
亚信安全2025年第1期《勒索家族和勒索事件监控报告》
本周态势快速感知 本周全球共监测到勒索事件51起,本周勒索事件数量降至近一年来最低,需注意防范。从整体上看Ransomhub依旧是影响最严重的勒索家族;本周Acrusmedia和Safepay也是两个活动频繁的恶意家族,需要注意防范。本周&#…...

【工具进阶】使用 Nmap 进行有效的服务和漏洞扫描
在渗透测试中,Nmap 是一款功能强大的经典工具。其应用场景广泛,包括主机发现、端口扫描、服务检测等。然而,要充分发挥 Nmap 的潜力,需要遵循科学的流程和规范。本文将为您详细介绍如何使用 Nmap 进行高效的渗透测试,同…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
