NLP CH3复习
CH3
3.1 几种损失函数

3.2 激活函数性质

3.3 哪几种激活函数会发生梯度消失

3.4 为什么会梯度消失



3.5 如何解决梯度消失和过拟合

3.6 梯度下降的区别
3.6.1 梯度下降(GD)
- 全批量:在每次迭代中使用全部数据来计算损失函数的梯度。
- 计算成本高:对于大数据集来说,每次迭代的计算成本非常高。
- 稳定收敛:由于每次都利用全部数据,因此梯度的估计非常准确,收敛路径平滑。
3.6.2 随机梯度下降(SGD)
- 单个样本:在每次迭代中随机选择一个数据样本来计算梯度。
- 计算成本低:每次只处理一个样本,大大减少了计算量。
- 收敛波动大:由于每次只用一个样本更新,梯度估计的方差较大,导致收敛过程中有较多波动。
3.6.3 Mini-batch梯度下降
- 小批量样本:在每次迭代中使用一小部分数据样本(例如32或64个样本)来计算梯度。
- 计算成本适中:平衡了全批量的计算效率和随机梯度的更新速度。
- 收敛相对稳定:小批量的使用减少了梯度估计的方差,使得收敛过程比随机梯度下降更稳定,但又比全批量梯度下降更灵活。
3.7 DNN
3.7.1 反向传播算法过程
将输出误差以某种形式反传给各层所有的单元,各层按本层误差修正各单元连接权值。


3.7.2 训练步骤

3.8 CNN
3.8.1 CNN的组成
由卷积层、子采样层、全连接层交叉堆叠而成
3.8.2 对比DNN
3.9 GNN

3.9.1 基本GNN和GCN的公式对比
3.9.1.1 基本GNN的公式
h v k = σ ( W k ∑ u ∈ N ( v ) h u k − 1 ∣ N ( v ) ∣ + B k h v k − 1 ) h_v^k = \sigma \left( W_k \sum_{u \in \mathcal{N}(v)} \frac{h_u^{k-1}}{|\mathcal{N}(v)|} + B_k h_v^{k-1} \right) hvk=σ Wku∈N(v)∑∣N(v)∣huk−1+Bkhvk−1
- 核心思想:
- 聚合节点 v v v 的邻居节点特征 h u k − 1 h_u^{k-1} huk−1 的平均值。
- 使用两个不同的权重矩阵 W k W_k Wk 和 B k B_k Bk 分别对邻居特征和节点自身特征进行线性变换。
- 通过激活函数 σ \sigma σ(例如 ReLU 或 tanh)引入非线性。
- 特点:
- 对所有邻居进行简单的平均(即 1 ∣ N ( v ) ∣ \frac{1}{|\mathcal{N}(v)|} ∣N(v)∣1),没有对邻居节点的重要性加权。
- 参数共享较少,特征变换对邻居和节点自身分开处理。
3.9.1.2 GCN的公式
h v k = σ ( W k ∑ u ∈ N ( v ) ∪ { v } h u k − 1 ∣ N ( u ) ∣ ∣ N ( v ) ∣ ) h_v^k = \sigma \left( W_k \sum_{u \in \mathcal{N}(v) \cup \{v\}} \frac{h_u^{k-1}}{\sqrt{|\mathcal{N}(u)||\mathcal{N}(v)|}} \right) hvk=σ Wku∈N(v)∪{v}∑∣N(u)∣∣N(v)∣huk−1
- 改进点:
- 归一化:
- 替代简单的平均聚合,GCN引入对称归一化因子 1 ∣ N ( u ) ∣ ∣ N ( v ) ∣ \frac{1}{\sqrt{|\mathcal{N}(u)||\mathcal{N}(v)|}} ∣N(u)∣∣N(v)∣1,减小高度节点(高度数节点)对结果的影响。
- 参数共享:
- 同一权重矩阵 W k W_k Wk 用于邻居特征和节点自身特征变换,减少参数数量,提高模型泛化能力。
- 自环(Self-loop):
- 邻域中加入节点自身(即 N ( v ) ∪ { v } \mathcal{N}(v) \cup \{v\} N(v)∪{v}),保证每层节点都能保留自身信息。
- 归一化:
- 特点:
- 更好的参数共享,减少了过拟合的风险。
- 归一化权重避免了高度数节点的特征主导问题。
3.9.2 GNN池化的概念
池化可以理解为图卷积过程中特征和节点的降维操作。以下是两种池化方式的相关描述:
3.9.2.1 全局池化
- 汇总整个图的节点特征,用于生成固定维度的图表示。
- 常见方式:
- 平均池化:取所有节点特征的平均值。
- 最大池化:取节点特征的最大值。
- 加权池化:根据任务需求对节点特征加权后聚合。
3.9.2.2 局部池化
- 在每一层中,通过选择部分重要节点,逐层减少图中节点的数量,同时保留主要的结构信息。
- 常见方式:
- Top- k k k池化:根据节点重要性评分选择得分最高的节点。
- 可微分池化(DiffPool):通过学习分配矩阵动态生成池化结果。
3.9.3 GCN的改进特点
-
参数共享(More parameter sharing):
- GCN使用相同的权重矩阵 W k W_k Wk 对邻居节点和自身节点的特征进行线性变换。
- 减少参数数量,提升模型训练稳定性。
-
削弱高度节点的影响(Down-weights high degree neighbors):
- 通过对称归一化因子 1 ∣ N ( u ) ∣ ∣ N ( v ) ∣ \frac{1}{\sqrt{|\mathcal{N}(u)||\mathcal{N}(v)|}} ∣N(u)∣∣N(v)∣1,减小度数大的节点对目标节点的特征贡献。
- 防止高度数节点主导聚合特征,造成模型偏差。
3.9.4 总结
- 基本GNN:通过简单平均的方式聚合邻居特征,参数较多,但未对邻居节点的贡献权重进行优化。
- GCN:引入对称归一化和参数共享机制,使模型更稳定、高效,同时减少过拟合。
- GNN池化:可以进一步通过全局或局部池化操作提取图或节点的高层次特征,适应更复杂的任务需求。
3.9.5 邻接节点个数不确定如何解决?
- 邻居信息聚合:
- 核心思想:将目标节点的特征更新为其自身特征和邻居特征的组合。
- 参数共享:
- GNN采用共享的权重矩阵(如图中的 W k W_k Wk 和 B k B_k Bk),即在同一层中所有节点使用相同的参数。
- 邻接节点特征聚合:
- 对每个节点的邻域进行聚合,生成一个固定维度的邻域表示(如 W k h k − 1 W_kh^{k-1} Wkhk−1)。

实心节点(蓝色圆点)代表的是实心结点(实际节点),它们是对应的实心结点的邻接结点聚集。
- 在原始图结构(左图)中,每个节点都有其自然的邻接关系(通过灰色线连接)
- 对于层次 h k h^k hk 到 h k − 1 h^{k-1} hk−1 之间的信息传递:
- 设定了锚点(实心节点)
- 使用注意力机制或聚合函数(图中通过 W k W_k Wk 和 B k B_k Bk 表示)来学习和聚集信息
- 将相邻节点的信息聚集到这些锚点上
- 具体的聚集过程:
- 通过权重矩阵 W k W_k Wk 来计算注意力分数或重要性权重
- 使用 B k B_k Bk 来转换或投影特征
- 最终将邻域节点的信息加权聚合到固定数量的锚点上
3.9.6 GNN训练,卷积步骤
在最后一层(K层)得到每个结点的表示后,可以根据任务将其代入任何损失函数,然后用梯度下降法训练参数。

3.10 RNN
- DNN、CNN 输入、输出定长;处理输入、输出变长问题效率不高。而自然语言处理中的语句通常其长度不固定。
- 单一DNN、CNN 无法处理时序相关序列问题
RNN核心思想:
- 将处理问题在时序上分解为一系列相同的“单元”,单元的神经网络可以在时序上展开,且能将上一时刻的结果传递给下一时刻,整个网络按时间轴展开。即可变长。

3.10.1 训练中的问题以及解决方式

会出现和深度前馈神经网络类似的梯度消失问题。在训练循环神经网络时,更经常出现的是梯度消失问题,训练较难

距当前节点越远的节点对当前节点处理影响越小,无法建模长时间的依赖
3.10.2 BPTT和BP的区别
参考链接
3.10.3 LSTM, GRU




3.10.4 设计题参考结构




补充
反向传播算法中第 L-1 层的误差项表达式:
δ ( L − 1 ) = σ ′ ( Z ( L − 1 ) ) ⋅ ( W ( L ) ) ⊤ δ ( L ) \delta^{(L-1)} = \sigma'(Z^{(L-1)}) \cdot (W^{(L)})^{\top} \delta^{(L)} δ(L−1)=σ′(Z(L−1))⋅(W(L))⊤δ(L)
其中:
- σ ′ \sigma' σ′ 表示激活函数的导数
- Z ( l ) Z^{(l)} Z(l) 是第 l 层的加权输入
- W ( l ) W^{(l)} W(l) 是第 l 层的权重矩阵
- δ ( l ) \delta^{(l)} δ(l) 是第 l 层的误差项
推导步骤:
-
前向传播定义
第 l 层的输出 A ( l ) A^{(l)} A(l) 表示为:
A ( l ) = σ ( Z ( l ) ) = σ ( W ( l ) A ( l − 1 ) + b ( l ) ) A^{(l)} = \sigma(Z^{(l)}) = \sigma(W^{(l)}A^{(l-1)} + b^{(l)}) A(l)=σ(Z(l))=σ(W(l)A(l−1)+b(l)) -
损失函数定义
使用均方误差(MSE)作为损失函数 J:
J = 1 2 ∥ A ( L ) − Y ∥ 2 J = \frac{1}{2} \|A^{(L)} - Y\|^2 J=21∥A(L)−Y∥2 -
计算输出层误差项 δ ( L ) \delta^{(L)} δ(L):
δ ( L ) = ∂ J ∂ Z ( L ) = ( A ( L ) − Y ) ⋅ σ ′ ( Z ( L ) ) \delta^{(L)} = \frac{\partial J}{\partial Z^{(L)}} = (A^{(L)} - Y) \cdot \sigma'(Z^{(L)}) δ(L)=∂Z(L)∂J=(A(L)−Y)⋅σ′(Z(L)) -
递推计算隐藏层误差项
对于第 l 层 (l = L-1, L-2, …, 1):
δ ( l ) = ∂ J ∂ Z ( l ) = ( W ( l + 1 ) ) ⊤ δ ( l + 1 ) ⋅ σ ′ ( Z ( l ) ) \delta^{(l)} = \frac{\partial J}{\partial Z^{(l)}} = (W^{(l+1)})^{\top} \delta^{(l+1)} \cdot \sigma'(Z^{(l)}) δ(l)=∂Z(l)∂J=(W(l+1))⊤δ(l+1)⋅σ′(Z(l))
具体到 l = L-1:
δ ( L − 1 ) = ( W ( L ) ) ⊤ δ ( L ) ⋅ σ ′ ( Z ( L − 1 ) ) \delta^{(L-1)} = (W^{(L)})^{\top} \delta^{(L)} \cdot \sigma'(Z^{(L-1)}) δ(L−1)=(W(L))⊤δ(L)⋅σ′(Z(L−1))
通过链式法则详细推导:
-
误差项 δ ( l ) \delta^{(l)} δ(l) 可表示为:
δ ( l ) = ∂ J ∂ Z ( l ) = ∂ J ∂ A ( l ) ⋅ ∂ A ( l ) ∂ Z ( l ) \delta^{(l)} = \frac{\partial J}{\partial Z^{(l)}} = \frac{\partial J}{\partial A^{(l)}} \cdot \frac{\partial A^{(l)}}{\partial Z^{(l)}} δ(l)=∂Z(l)∂J=∂A(l)∂J⋅∂Z(l)∂A(l) -
其中:
- ∂ A ( l ) ∂ Z ( l ) = σ ′ ( Z ( l ) ) \frac{\partial A^{(l)}}{\partial Z^{(l)}} = \sigma'(Z^{(l)}) ∂Z(l)∂A(l)=σ′(Z(l))
- ∂ J ∂ A ( l ) = ( W ( l + 1 ) ) ⊤ δ ( l + 1 ) \frac{\partial J}{\partial A^{(l)}} = (W^{(l+1)})^{\top} \delta^{(l+1)} ∂A(l)∂J=(W(l+1))⊤δ(l+1)
-
最终得到第 L-1 层的误差项:
δ ( L − 1 ) = σ ′ ( Z ( L − 1 ) ) ⋅ ( W ( L ) ) ⊤ δ ( L ) \delta^{(L-1)} = \sigma'(Z^{(L-1)}) \cdot (W^{(L)})^{\top} \delta^{(L)} δ(L−1)=σ′(Z(L−1))⋅(W(L))⊤δ(L)
第 L-1 层的误差是由第 L 层的权重矩阵和误差项传递,并与第 L-1 层激活函数的导数相乘得到的。
相关文章:

NLP CH3复习
CH3 3.1 几种损失函数 3.2 激活函数性质 3.3 哪几种激活函数会发生梯度消失 3.4 为什么会梯度消失 3.5 如何解决梯度消失和过拟合 3.6 梯度下降的区别 3.6.1 梯度下降(GD) 全批量:在每次迭代中使用全部数据来计算损失函数的梯度。计算成本…...

BurpSuite2024.11
新增功能 2024 年 11 月 25 日,版本 24.11 此版本引入了站点地图过滤器 Bambdas、匹配和替换 Bambdas、用于 API 扫描的动态身份验证令牌,以及用于入侵者攻击的增强负载管理。我们还进行了多项用户体验改进、性能改进和一些错误修复。 使用 Bambdas 过…...
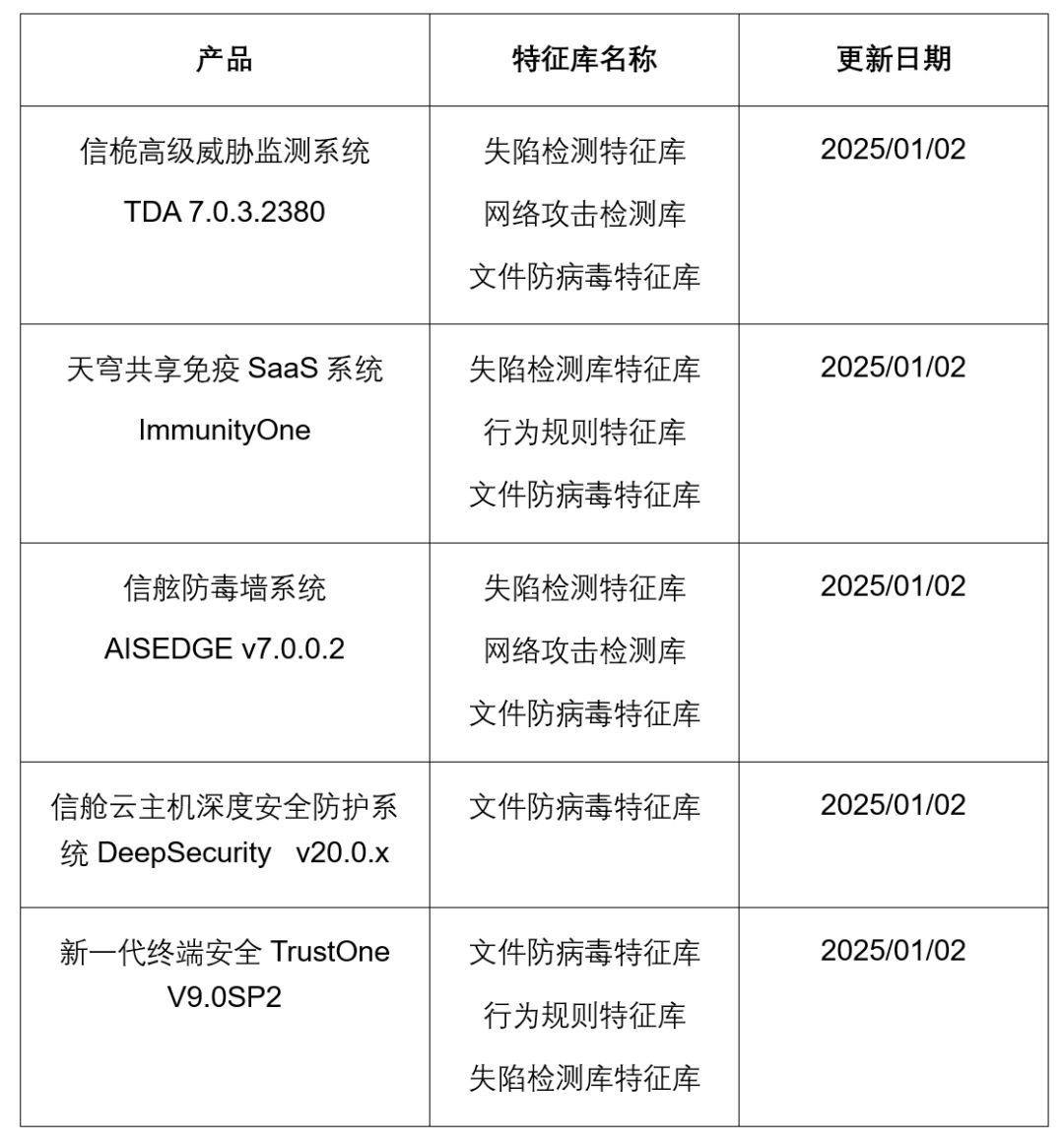
亚信安全2025年第1期《勒索家族和勒索事件监控报告》
本周态势快速感知 本周全球共监测到勒索事件51起,本周勒索事件数量降至近一年来最低,需注意防范。从整体上看Ransomhub依旧是影响最严重的勒索家族;本周Acrusmedia和Safepay也是两个活动频繁的恶意家族,需要注意防范。本周&#…...

【工具进阶】使用 Nmap 进行有效的服务和漏洞扫描
在渗透测试中,Nmap 是一款功能强大的经典工具。其应用场景广泛,包括主机发现、端口扫描、服务检测等。然而,要充分发挥 Nmap 的潜力,需要遵循科学的流程和规范。本文将为您详细介绍如何使用 Nmap 进行高效的渗透测试,同…...

【工具推荐】XSS 扫描器-XSStrike
介绍 XSStrike 是一个跨站点脚本检测套件,配备四个手写解析器、一个智能有效载荷生成器、一个强大的模糊测试引擎以及速度极快的爬虫。XSStrike 不会像其他工具一样注入有效载荷并检查其是否有效,而是使用多个解析器分析响应,然后通过与模糊…...
)
Spring Boot 各种事务操作实战(自动回滚、手动回滚、部分回滚)
概念 事务定义 事务,就是一组操作数据库的动作集合。事务是现代数据库理论中的核心概念之一。如果一组处理步骤或者全部发生或者一步也不执行,我们称该组处理步骤为一个事务。当所有的步骤像一个操作一样被完整地执行,我们称该事务被提交。…...

Zabbix5.0版本(监控Nginx+PHP服务状态信息)
目录 1.监控Nginx服务状态信息 (1)通过Nginx监控模块,监控Nginx的7种状态 (2)开启Nginx状态模块 (3)配置监控项 (4)创建模板 (5)用默认键值…...

C# 设计模式概况
什么是设计模式 大家熟知的GOF23种设计模式,源自《Design Patterns: Elements of Reusable Object-Oriented Software》一书,由 Erich Gamma、Richard Helm、Ralph Johnson 和 John Vlissides 合著,四人组Gang of Four简称GOF。总结了在面向…...

Nginx 配置 SSL(HTTPS)详解
Nginx作为一款高性能的HTTP和反向代理服务器,自然支持SSL/TLS加密通信。本文将详细介绍如何在Nginx中配置SSL,实现HTTPS的访问。 随着互联网安全性的日益重要,HTTPS协议逐渐成为网站加密通信的标配。Nginx作为一款高性能的HTTP和反向代理服务…...

论文解读之Generative Dense Retrieval: Memory Can Be a Burden
本次论文解读,博主带来生成式稠密检索:记忆可能成为一种负担的论文分享 一、简介 生成式检索根据给定的查询,自回归地检索相关的文档标识符,在小规模的文档库中表现不错,通过使用模型参数记忆文档库,生成…...

RTC:实时时钟
RTC:实时时钟 1、实时时钟2、闹钟中断3、秒中断4、输出功能5、BKP的读写6、BKP的侵入事件 1、实时时钟 ①RTC.c #include "RTC.h"/*** brief:RTC初始化函数*/ RCC_PeriphCLKInitTypeDef RTCPeriphClkInit; //RTC时钟配置结构体 RTC_HandleT…...

mqtt python rtsp拉流图传测试
GitHub - robmarkcole/mqtt-camera-streamer: Stream images from a connected camera over MQTT, view using Streamlit, record to file and sqlite 用这个项目,按照readme配置,把config里面的ip配置成接收端的ip地址。 该装的包装完之后,…...

win32汇编环境,对话框程序中通过资源显示bmp图像
;运行效果 ;win32汇编环境,对话框程序中通过资源显示bmp图像 ;通过资源的方式,会把图像固定在exe文件里,会变大。通过读取文件的方式,没有固定在exe文件里,也可以随时换图像文件,所以exe文件较小 ;直接抄进RadAsm可编译…...

《探索人工智能的多元学派:符号主义、连接主义与行为主义》
在人工智能发展的进程中,不同学派从各自的角度诠释着智能的本质。其中符号主义、连接主义和行为主义学派占据着重要地位,它们以独特的方式推动着人工智能的发展。 符号主义学派:逻辑推理的核心 符号主义学派认为人工智能源于对逻辑符号的处…...

2024年终总结及计划
24年收获不少,早就想总结下,但是有的问题不想去思考,也不想去面对,就晚了几天,趁着加班总结反思下。 一、计划完成情况 1、生活 ①运动:继续坚持每周慢跑15公里,这是必须要做的。另外&#x…...

数据挖掘——关联规则挖掘
数据挖掘——关联数据挖掘 关联数据挖掘关联规则关联规则挖掘问题:具体挖掘过程Apriori 产生关联规则 关联数据挖掘 关联分析用于发现隐藏在大型数据集中的令人感兴趣的联系,所发现的模式通常用关联规则或频繁项集的形式表示。 关联规则反映一个事物与…...

JVM实战—9.线上FGC的几种案例
大纲 1.如何优化每秒十万QPS的社交APP的JVM性能(增加S区大小 优化内存碎片) 2.如何对垂直电商APP后台系统的FGC进行深度优化(定制JVM参数模版) 3.不合理设置JVM参数可能导致频繁FGC(优化反射的软引用被每次YGC回收) 4.线上系统每天数十次FGC导致频繁卡顿的优化(大对象问题…...
STM32-BKP备份寄存器RTC实时时钟
一、原理 Unix: 一些系统是使用32bit有符号数存储,实际范围为-2,147,483,648到2,147,483,647即~ 经过计算int32数据会在2038年1月19日溢出,可以看到转换的为北京时间。 STM32的时间戳为无符号时间戳。 我们需要把秒计数器的时间通过计算…...

HTML-文本标签
历史上,网页的主要功能是文本展示。所以,HTML 提供了大量的文本处理标签。 1.<div> <div>是一个通用标签,表示一个区块(division)。它没有语义,如果网页需要一个块级元素容器,又没…...

香橙派5plus单独编译并安装linux内核无法启动的原因分析与解决记录
1 说明 我依照官方手册编译单独编译linux内核,安装后重启出现内核启动失败的问题,编译和安装步骤如下:# 1. 克隆源码 git clone --depth1 -b orange-pi-6.1-rk35xx https://github.com/orangepi-xunlong/linux-orangepi# 2 配置源码 make rockchip_linu…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
