高等数学学习笔记 ☞ 连续函数的运算与性质
1. 连续函数的运算
1. 连续函数的四则运算:
(1)若函数在点
处连续,则函数
在点
处也连续。
(2)若函数在区间
上连续,则函数
在区间
上也连续。
2. 反函数的连续性:
若函数在定义域
上是单调且连续的,那么其反函数
在定义域
上
也是单调且连续的。
备注:上述声明函数
必须是单调的,目的是保证函数
存在反函数。
3. 复合函数的连续性:
已知函数在
处连续,函数
在
处连续,那么函数
在
处连续。
与此同时,有:。
复合函数在该点连续时才能使用此公式。
备注:复合函数:通俗地说就是函数套函数,是把几个简单的函数复合为一个较为复杂的函数。
4. (基本)初等函数的连续性:
(1)基本初等函数在其定义域内是连续的。 (2)初等函数在其定义域内是连续的。
备注:
①:初等函数:由基本初等函数经过有限次的加、减、乘、除、有理数次乘方、有理数次开方以及有限次函数复合而产生,
并且可以用一个解析式表达的函数。
②:幂指函数:形如
的函数。幂指函数不属于初等函数,属于复合函数,常用处理方式:
。
2. 闭区间上连续函数的性质
1. 最值与最值点:最大值(点)与最小值(点)
(1)最大值:设函数的定义域为
,存在
,对于
,都有
,则称
是函数
的最大值。
(2)最小值:设函数的定义域为
,存在
,对于
,都有
,则称
是函数
的最小值。
(3)最大值点:函数取得最大值时所对应的点,称为最大值点。
(4)最小值点:函数取得最小值时所对应的点,称为最小值点。
备注:
①:函数
的最大值与最小值是可以不存在的,比如单调函数在区间端点无定义。
②:若函数
的最大值与最小值存在,那么最大值和最小值是唯一的,是可以相等的,但最大值要大于等于最小值。
③:若函数
的最大值与最小值存在,那么最大值点和最小值点不一定是唯一的。
2. 闭区间上连续函数的性质:
(1)最大值和最小值定理:在闭区间上连续的函数,一定存在最大值和最小值。
(2)有界性定理:在闭区间上连续的函数,在该区间上一定有界。
(3)零点定理:设函数在闭区间
上是连续的,若
是异号的(即:
),
则至少存在一点,使得
。
备注:零点:若函数
,那么称
是函数
的零点。
(4)介值定理:设函数在闭区间
上是连续的,
,
,对于
与
间的任意数
,
则至少存在一点,使得
。
推论:设函数在闭区间
上是连续的,函数
在闭区间
上的最小值和最大值分别为
,
①:则函数的值域为
。
②:对于,则至少存在
,使得
。
相关文章:
高等数学学习笔记 ☞ 连续函数的运算与性质
1. 连续函数的运算 1. 连续函数的四则运算: (1)若函数在点处连续,则函数在点处也连续。 (2)若函数在区间上连续,则函数在区间上也连续。 2. 反函数的连续性: 若函数在定义域上是单…...

k8s基础(4)—Kubernetes-Service
Service概述 抽象层 k8s的Service是一种抽象层,用于为一组具有相同功能的Pod提供一个统一的入口地址,并通过负载均衡将网络流量分发到这些Pod上。 Service解决了Pod动态变化的问题,例如Pod的IP地址和端口可能会发生变化,通过…...

CAN或者CANFD的Busoff的恢复时间会受到报文周期的影响么?
目录 分析恢复机制角度快恢复和慢恢复策略角度特殊情况分析分析 Busoff的恢复时间通常不会直接受到报文周期的影响,以下是具体分析: 恢复机制角度 CAN总线的节点在Busoff状态下,恢复过程主要是等待总线上出现128个连续的11bit隐性位,与报文周期并无直接关联。无论报文周…...

【DevOps】Jenkins部署
Jenkins部署 文章目录 Jenkins部署资源列表基础环境一、部署Gilab1.1、安装Gitlab1.2、修改配置文件1.3、加载配置文件1.4、访问Gitlab1.5、修改root登录密码1.6、创建demo测试项目1.7、上传代码1.8、验证上传的代码 二、部署Jenkins所需软件2.1、部署JDK2.2、部署Tomcat2.3、部…...

【MATLAB第112期】基于MATLAB的SHAP可解释神经网络回归模型(敏感性分析方法)
【MATLAB第112期】基于MATLAB的SHAP可解释神经网络回归模型(敏感性分析方法) 引言 该文章实现了一个可解释的神经网络回归模型,使用BP神经网络(BPNN)来预测特征输出。该模型利用七个变量参数作为输入特征进行训练。为…...

【Shell编程 / 4】函数定义、脚本执行与输入输出操作
文章目录 函数 与 脚本定义函数示例:简单的 Shell 函数函数参数返回值 脚本执行创建脚本执行脚本 输入输出输出:echo 和 printf输入:read 命令 命令行参数示例:传递参数 函数 与 脚本 在 Shell 编程中,函数和脚本是组…...

RK3588+麒麟国产系统+FPGA+AI在电力和轨道交通视觉与采集系统的应用
工业视觉识别系统厂家提供的功能主要包括: 这些厂家通过先进的视觉识别技术,实现图像的采集、处理与分析。系统能够自动化地完成质量检测、物料分拣、设备监控等任务,显著提升生产效率和产品质量。同时,系统具备高度的灵活性和可扩…...

MySQL 01 02 章——数据库概述与MySQL安装篇
一、数据库概述 (1)为什么要使用数据库 数据库可以实现持久化,什么是持久化:数据持久化意味着将内存中的数据保存到硬盘上加以“固化”持久化的主要作用是:将内存中的数据存储在关系型数据库中,当然也可以…...

运行framework7
安装 framework7 下载地址https://gitcode.com/gh_mirrors/fr/framework7-vue node 下载 https://nodejs.cn/#ionic 配置npm 的镜像源 npm config set registry https://registry.npmmirror.com 下载nvm 进行nvm管理https://www.downza.cn/soft/352547.html 我一开始使用node…...

【Web】软件系统安全赛CachedVisitor——记一次二开工具的经历
明天开始考试周,百无聊赖开了一把CTF,还顺带体验了下二开工具,让无聊的Z3很开心🙂 CachedVisitor这题 大概描述一下:从main.lua加载一段visit.script中被##LUA_START##(.-)##LUA_END##包裹的lua代码 main.lua loca…...

实现自定义集合类:深入理解C#中的IEnumerable<T>接口
文章目录 介绍主要成员示例代码约束常见的约束类型示例代码介绍 在C#中,IEnumerable<T> 是一个泛型接口,用于表示可以被枚举的集合。它定义了用于遍历集合中元素的方法和属性。IEnumerable<T> 是 IEnumerable 的泛型版本,提供了类型安全的枚举功能。 当我们实…...

Compression Techniques for LLMs
Compression Techniques for LLMs 随着大型语言模型(LLMs)的迅速发展,提高其计算效率和存储效率成为研究的重要方向。为了实现这一目标,诸多压缩技术应运而生。本文将深入探讨几种有效的压缩技术,这些技术不仅能够降低…...
)
Nexus Message Transaction Services(MTS)
Nexus 系列交换机遇到以下情形时,可以尝试查看是否是 MTS 消息卡在缓冲区过多,因为 MTS 负责处理模块内以及跨模块(包括跨管理引擎)的各服务之间的消息路由和排队。 • CPU 高 • 命令行无响应、响应慢 • 控制平面中断 • 流量问…...
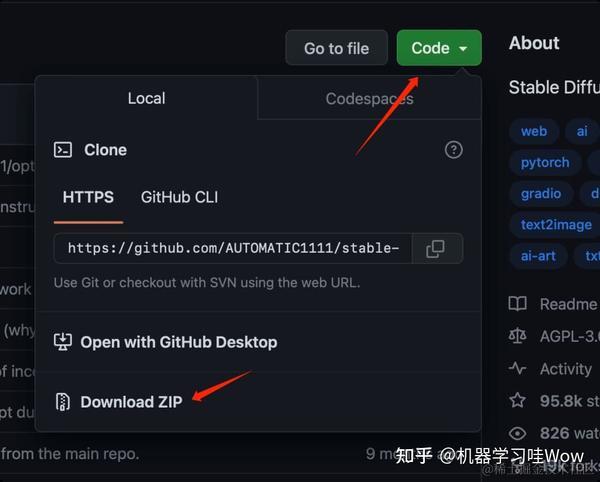
2025年Stable Diffusion安装教程(超详细)
StableDiffusion的安装部署其实并不困难,只需简单点击几下,几分钟就能安装好,不管是windows还是苹果mac电脑,关于StableDiffusion的各种安装方式,这片文章一一来给大家讲明白。(所有安装资料都给大家整理好…...

力扣【SQL连续问题】
180. 连续出现的数字 SELECT DISTINCT if(a.num b.num AND b.num c.num,a.num,null) AS ConsecutiveNums FROM Logs a LEFT OUTER JOIN Logs b ON a.id1 b.id LEFT OUTER JOIN Logs c ON a.id2 c.id WHERE if(a.num b.num AND b.num c.num,a.num,null) IS NOT NULL603. 连…...

深圳市-地铁线路和站点名称shp矢量数据(精品)2021年-2030最新arcmap含规划路线内容测评分析
深圳市的地铁网络是城市公共交通系统的重要组成部分,随着城市的发展,其规模和覆盖范围也在不断扩大。这份"深圳市-地铁线路和站点名称shp矢量数据(精品)2021年-2030最新arcmap含规划路线.zip"压缩包提供了全面而详细的信…...

企业级网络运维管理系统深度解析与实践案例
企业级网络运维管理系统深度解析与实践案例 在当今这个信息化时代,企业网络系统的稳定运行和高效管理成为了业务持续发展和创新的关键。企业级网络运维管理系统作为支撑这一目标的基石,其重要性不言而喻。本文将深入探讨企业级网络运维管理系统的构建原则、关键组件、实施步…...

音视频入门基础:MPEG2-PS专题(5)——FFmpeg源码中,解析PS流中的PES流的实现
一、引言 从《音视频入门基础:MPEG2-PS专题(3)——MPEG2-PS格式简介》中可以知道,PS流由一个个pack(包装)组成。一个pack 一个pack_header 一个或多个PES_packet。pack_header中还可能存在system header…...

【问题记录】npm create vue@latest报错
1,错误日志 npm error code EPERM npm error syscall mkdir npm error path D:\Program Files\nodejs\node_cache\_cacache npm error errno EPERM npm error FetchError: Invalid response body while trying to fetch https://registry.npmjs.org/create-vue: EP…...

OpenGL材质系统和贴图纹理
上一篇文章当中笔者为大家介绍了风氏光照模型,相信大家也发现了光照着色器当中有设置有很多控制光照强度的参数,而所谓的材质系统就是我们可以人为的去调节这些参数,让一个物体的反光效果能够更加接近我们现实生活当中的一些物体。 材质系统…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
