Math Reference Notes: 积分因子
在求解一阶线性微分方程时,积分因子(Integrating Factor)是一个非常重要的工具,它能够将复杂的微分方程转化为一个可以直接积分的形式。通过使用积分因子,我们可以简化微分方程的结构,使得求解过程更加直接和有效。
1. 一阶线性微分方程的标准形式
首先,回顾一下 一阶线性微分方程 的标准形式,它通常写作:
d y d x + P ( x ) y = Q ( x ) \frac{dy}{dx} + P(x) y = Q(x) dxdy+P(x)y=Q(x)
其中, y y y 是未知函数, P ( x ) P(x) P(x) 和 Q ( x ) Q(x) Q(x) 是已知函数。我们的目标是通过合适的技巧来解这个方程。直接求解这个方程通常是比较困难的,尤其是当方程中包含了未知函数 (y) 和它的导数。
2. 积分因子的引入
为了简化这个微分方程,我们引入了 积分因子,它是一个与 x x x 有关的函数 μ ( x ) \mu(x) μ(x),我们将原方程两边都乘以它。我们希望通过这种方式,使得微分方程的左边可以变成一个完整的导数形式。
-
步骤一:乘以积分因子
设积分因子为 μ ( x ) \mu(x) μ(x),我们将方程两边同时乘以它:
μ ( x ) d y d x + μ ( x ) P ( x ) y = μ ( x ) Q ( x ) \mu(x) \frac{dy}{dx} + \mu(x) P(x) y = \mu(x) Q(x) μ(x)dxdy+μ(x)P(x)y=μ(x)Q(x)
左边的第一个项是 μ ( x ) d y d x \mu(x) \frac{dy}{dx} μ(x)dxdy,而第二项是 μ ( x ) P ( x ) y \mu(x) P(x) y μ(x)P(x)y。我们希望将左边的两项合并成一个完整的导数形式。
-
步骤二:使左边变成全微分
根据乘积法则 d d x ( u ( x ) v ( x ) ) = u ( x ) d v d x + v ( x ) d u d x \frac{d}{dx}(u(x)v(x)) = u(x)\frac{dv}{dx} + v(x)\frac{du}{dx} dxd(u(x)v(x))=u(x)dxdv+v(x)dxdu,我们希望找到一个 μ ( x ) \mu(x) μ(x),使得:
μ ( x ) d y d x + μ ′ ( x ) y = d d x ( μ ( x ) y ) \mu(x) \frac{dy}{dx} + \mu'(x) y = \frac{d}{dx} \left( \mu(x) y \right) μ(x)dxdy+μ′(x)y=dxd(μ(x)y)
这一步骤的关键是使用 乘积法则。比较两边的表达式,我们发现:
μ ′ ( x ) = μ ( x ) P ( x ) \mu'(x) = \mu(x) P(x) μ′(x)=μ(x)P(x)
这是一个简单的分离变量微分方程,可以通过分离变量法得到 μ ( x ) \mu(x) μ(x) 的表达式。
-
步骤三:求解积分因子
为了求解 μ ( x ) \mu(x) μ(x),我们将上式重写为:
μ ′ ( x ) μ ( x ) = P ( x ) \frac{\mu'(x)}{\mu(x)} = P(x) μ(x)μ′(x)=P(x)
这是一个标准的可分离变量微分方程,解这个方程得到:
ln ∣ μ ( x ) ∣ = ∫ P ( x ) d x \ln|\mu(x)| = \int P(x) \, dx ln∣μ(x)∣=∫P(x)dx
从而,积分因子的解为:
μ ( x ) = e ∫ P ( x ) d x \mu(x) = e^{\int P(x) \, dx} μ(x)=e∫P(x)dx
3. 为什么选择 e ∫ P ( x ) d x e^{\int P(x) \, dx} e∫P(x)dx 作为积分因子
选择 e ∫ P ( x ) d x e^{\int P(x) \, dx} e∫P(x)dx 作为积分因子的原因如下:
-
指数函数的微分性质:指数函数 (e^x) 有非常简洁的微分性质,特别是对于 e f ( x ) e^{f(x)} ef(x),我们有: d d x e f ( x ) = e f ( x ) f ′ ( x ) \frac{d}{dx} e^{f(x)} = e^{f(x)} f'(x) dxdef(x)=ef(x)f′(x)
这使得指数函数在微分运算中非常方便,能够与其他函数配合,形成简洁的导数形式。 -
指数函数的常数因子属性
使用指数函数 e ∫ P ( x ) d x e^{\int P(x) \, dx} e∫P(x)dx 作为积分因子的另一个重要原因是,它能够有效地处理常数因子。对于积分因子 e ∫ P ( x ) d x e^{\int P(x) \, dx} e∫P(x)dx,我们可以通过选择合适的积分常数 C C C 来调节解的形式。这是因为:
e ∫ P ( x ) d x + C = e C e ∫ P ( x ) d x e^{\int P(x) \, dx + C} = e^C e^{\int P(x) \, dx} e∫P(x)dx+C=eCe∫P(x)dx
由于 e C e^C eC 是一个常数,它不会影响微分方程的解结构,因此 e ∫ P ( x ) d x e^{\int P(x) \, dx} e∫P(x)dx 为我们提供了一个非常灵活的工具,使得我们能够找到合适的解。
-
指数函数的积累性质与线性性
在微分方程中,特别是一阶线性微分方程中,我们通过积分因子 e ∫ P ( x ) d x e^{\int P(x) \, dx} e∫P(x)dx 来将原方程转化为更容易求解的形式。在这种过程中,积分因子的形式为 e ∫ P ( x ) d x e^{\int P(x) \, dx} e∫P(x)dx 是为了利用指数函数的“积累性质”(即它的导数与本身成比例)来简化方程的求解。
因为指数函数是线性方程的解的自然形式,它允许我们将微分方程转化为一个完全导数形式,使得后续的积分步骤更加简洁和直接。通过这种方式,左边的微分变得容易处理,右边的积分也能够简单地求得,从而简化了求解过程。
-
数学的普遍性与简洁性
虽然可以选择其他形式的积分因子,但指数函数的选择是基于其在微积分中的普遍性与简洁性。其他函数形式(如幂函数、对数函数等)通常不能像指数函数那样在微分运算中保持简洁性,且往往无法使方程转化为完整的微分形式。因此,指数函数 e ∫ P ( x ) d x e^{\int P(x) \, dx} e∫P(x)dx 是一个非常自然的选择,符合数学中求解线性微分方程的常见技巧。
4. 通过积分因子求解微分方程
现在,我们可以继续通过乘以积分因子来求解原方程。
-
将方程两边乘以积分因子:
μ ( x ) d y d x + μ ( x ) P ( x ) y = μ ( x ) Q ( x ) \mu(x) \frac{dy}{dx} + \mu(x) P(x) y = \mu(x) Q(x) μ(x)dxdy+μ(x)P(x)y=μ(x)Q(x)
-
左边变为全微分形式:
d d x ( μ ( x ) y ) = μ ( x ) Q ( x ) \frac{d}{dx} (\mu(x) y) = \mu(x) Q(x) dxd(μ(x)y)=μ(x)Q(x)
-
对两边进行积分:
μ ( x ) y = ∫ μ ( x ) Q ( x ) d x + C \mu(x) y = \int \mu(x) Q(x) \, dx + C μ(x)y=∫μ(x)Q(x)dx+C
-
解得 y y y 的表达式:
y = 1 μ ( x ) ( ∫ μ ( x ) Q ( x ) d x + C ) y = \frac{1}{\mu(x)} \left( \int \mu(x) Q(x) \, dx + C \right) y=μ(x)1(∫μ(x)Q(x)dx+C)
通过这个过程,我们得到了原微分方程的通解。
5. 实际例子
考虑方程:
d y d x + 2 y = x \frac{dy}{dx} + 2y = x dxdy+2y=x
这是一个一阶线性微分方程,其中 P ( x ) = 2 P(x) = 2 P(x)=2 和 Q ( x ) = x Q(x) = x Q(x)=x。我们首先计算积分因子:
μ ( x ) = e ∫ 2 d x = e 2 x \mu(x) = e^{\int 2 \, dx} = e^{2x} μ(x)=e∫2dx=e2x
将方程两边乘以 μ ( x ) = e 2 x \mu(x) = e^{2x} μ(x)=e2x:
e 2 x d y d x + 2 e 2 x y = x e 2 x e^{2x} \frac{dy}{dx} + 2 e^{2x} y = x e^{2x} e2xdxdy+2e2xy=xe2x
左边可以写成:
d d x ( e 2 x y ) = x e 2 x \frac{d}{dx} (e^{2x} y) = x e^{2x} dxd(e2xy)=xe2x
对两边积分得到:
e 2 x y = ∫ x e 2 x d x + C e^{2x} y = \int x e^{2x} \, dx + C e2xy=∫xe2xdx+C
通过分部积分法求解积分,可以得到:
e 2 x y = 1 2 x e 2 x − 1 4 e 2 x + C e^{2x} y = \frac{1}{2} x e^{2x} - \frac{1}{4} e^{2x} + C e2xy=21xe2x−41e2x+C
最终解为:
y = 1 2 x − 1 4 + C e − 2 x y = \frac{1}{2} x - \frac{1}{4} + C e^{-2x} y=21x−41+Ce−2x
这是原方程的通解。
相关文章:

Math Reference Notes: 积分因子
在求解一阶线性微分方程时,积分因子(Integrating Factor)是一个非常重要的工具,它能够将复杂的微分方程转化为一个可以直接积分的形式。通过使用积分因子,我们可以简化微分方程的结构,使得求解过程更加直接…...

解决7-Zip图标更换问题
手动美化7-Zip图标,告别Win95风格 之前下载的7z压缩的文件图标都是软件的黑白图形,但是电脑重置了默认应用后再改回7z,压缩的文件就变成黄色的图标了,试过很多问题,尝试过手动更改图标,或者代码更改&#…...

Java 性能监控工具详解:JConsole、VisualVM 和 Java Mission Control
在 Java 应用程序的开发和维护过程中,性能监控和故障诊断是至关重要的。本文将详细介绍三款常用的 Java 性能监控工具:JConsole、VisualVM 和 Java Mission Control(JMC),并探讨它们的功能和使用方法。 1 JConsole 1…...

浏览器报错:您的连接不是私密连接,Kubernetes Dashboard无法打开
问题描述 部署完成Kubernetes Dashboard后,打开HTTPS的web页面,Chrome和Edge浏览器都无法正常加载页面,会提示您的连接不是私密连接的报错。 原因: 浏览器不信任这些自签名的ssl证书,为了…...

用Python进行大数据处理:如何使用pandas和dask处理海量数据
《Python OpenCV从菜鸟到高手》带你进入图像处理与计算机视觉的大门! 解锁Python编程的无限可能:《奇妙的Python》带你漫游代码世界 随着数据量的爆炸式增长,大数据处理成为现代数据科学和工程领域的核心挑战。Python作为数据分析的重要工具,其生态系统中的pandas和dask库…...

机器人手眼标定
机器人手眼标定 一、机器人手眼标定1. 眼在手上标定基本原理2. 眼在手外标定基本原理 二、眼在手外标定实验三、标定精度分析 一、机器人手眼标定 要实现由图像目标点到实际物体上抓取点之间的坐标转换,就必须拥有准确的相机内外参信息。其中内参是相机内部的基本参…...

基于Springboot + vue实现的校园失物招领系统
🥂(❁◡❁)您的点赞👍➕评论📝➕收藏⭐是作者创作的最大动力🤞 💖📕🎉🔥 支持我:点赞👍收藏⭐️留言📝欢迎留言讨论 🔥🔥&…...
)
关于C语言初步的一些基础知识整理(2)
“本篇是对于C语言初步中一些基础知识的简单整理,内容较为琐碎,但实用” 在C语言中,格式控制符是用于指定数据输出格式的特殊字符,不同的数据类型有着其对应的格式控制符。具体的: %f 用于输出浮点型数据(…...

Linux驱动开发:深入理解I2C时序(二)
在Linux驱动开发中,I2C时序的理解和正确处理是保证I2C设备正常工作和通信的关键。I2C协议的时序特性决定了数据的有效传输和设备间的协作。因此,掌握I2C的时序细节,以及如何在Linux内核中进行时序处理,能够让开发者更好地处理设备通信问题。 本文将继续深入探讨I2C通信协议…...

逆向安卓抓包
打开Mumu网易,打开设置,打开其他,开启root权限 打开Mumu网易,找到apk安装藏航准备网.apk charles配置:proxy setting 端口9888 查看当地IP:help--->local IP address SSL Proxying Setting--->Add---->IP…...

Spring源码分析之事件机制——观察者模式(一)
目录 事件基类定义 事件监听器接口 事件发布者接口及实现 事件广播器实现 小小总结 Spring源码分析之事件机制——观察者模式(一)-CSDN博客 Spring源码分析之事件机制——观察者模式(二)-CSDN博客 Spring源码分析之事件机制…...

QT实现 端口扫描暂停和继续功能 3
上篇QT给端口扫描工程增加线程2-CSDN博客 为按钮pushButton_Stop添加clicked事件,功能为暂停扫描,并在暂停后显示继续按钮,点击继续按钮之后继续扫描 1.更新UI 添加继续按钮 点击转到槽则会自动声明 2. 更新 MainWindow.h 需要新增的部分…...

SHViT模型详解
模型简介 SHViT是一种创新的 单头视觉Transformer ,旨在优化计算效率和内存使用。它的核心设计理念围绕着消除传统视觉Transformer架构中的冗余元素,特别关注宏观和微观设计层面的问题。 SHViT采用了 1616的大跨度patchify stem 和 3阶段结构 ,这种独特的设计不仅有效减少…...

QGIS Server安装部署教程
一、QGIS 安装部署 1、下载安装QGIS链接如下图,选择最新的安装包文件QGIS-OSGeo4W-3.34.14-1.msi,下载完成后运行安装。 2、安装时选择QGIS安装路径不要带空格,此处会影响QGIS Server安装运行。 3、安装过程省略,安装完成后打…...

基于 Apache Commons Pool 实现的 gRPC 连接池管理类 GrpcChannelPool 性能分析与优化
基于 Apache Commons Pool 实现的 gRPC 连接池管理类 GrpcChannelPool 性能分析与优化 1. 输出关键信息的代码示例 日志记录方法 使用以下代码记录连接池的关键信息,帮助分析连接池的状态和性能瓶颈: import org.apache.commons.pool2.impl.GenericO…...

【C语言】
目录 第一个C语言程序题目实际应用程序要求输入描述输出描述示例 程序实现三级目录 第一个C语言程序 打开VS创建项目(视图-解决方案管理器)创建源文件(后缀.c).c会按照C的语言编译代码 c #include <stdio.h> //std-标准 //…...

标题:利用Spring Boot构建JWT刷新令牌应用
标题:利用Spring Boot构建JWT刷新令牌应用 去发现同类优质开源项目:https://gitcode.com/ 一、项目介绍 在Java开发中,Spring Boot以其简洁的配置和强大的功能深受开发者喜爱。Spring Boot Refresh Token with JWT 是一个开源示例项目,它展…...

性能测试工具的原理与架构解析
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 在软件开发与运维领域,性能测试是确保系统稳定、高效运行的关键环节。性能测试工具作为实现这一目标的重要工具,通过模拟真实用户行为和负载…...

基于STM32的自动水满报警系统设计
目录 引言系统设计 硬件设计软件设计系统功能模块 水位检测模块报警模块自动控制模块控制算法 水位检测逻辑报警触发逻辑代码实现 水位检测模块报警控制模块自动控制逻辑系统调试与优化结论与展望 1. 引言 水满报警系统在家庭、农业、工业等领域广泛应用,通过实时…...

C语言 数组编程练习
1.将数组A的内容和数组B中的内容进行交换。(数组一样大) 2.创建一个整形数组,完成对数组的操作 实现函数Init()初始化数组全为0 实现print()打印数组的每个元素 实现reverse()函数完成数组元素的逆置 //2.创建一个整形数组,完…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...
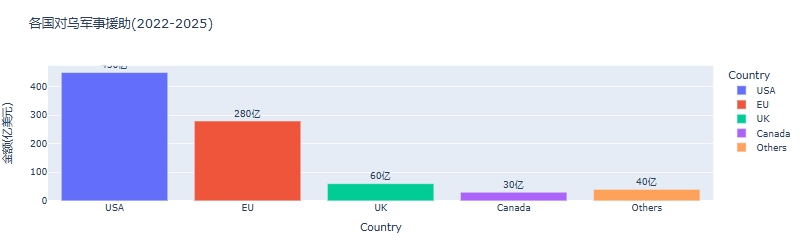
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...

Vue 实例的数据对象详解
Vue 实例的数据对象详解 在 Vue 中,数据对象是响应式系统的核心,也是组件状态的载体。理解数据对象的原理和使用方式是成为 Vue 专家的关键一步。我将从多个维度深入剖析 Vue 实例的数据对象。 一、数据对象的定义方式 1. Options API 中的定义 在 Options API 中,使用 …...

IP选择注意事项
IP选择注意事项 MTP、FTP、EFUSE、EMEMORY选择时,需要考虑以下参数,然后确定后选择IP。 容量工作电压范围温度范围擦除、烧写速度/耗时读取所有bit的时间待机功耗擦写、烧写功耗面积所需要的mask layer...

Centos 7 服务器部署多网站
一、准备工作 安装 Apache bash sudo yum install httpd -y sudo systemctl start httpd sudo systemctl enable httpd创建网站目录 假设部署 2 个网站,目录结构如下: bash sudo mkdir -p /var/www/site1/html sudo mkdir -p /var/www/site2/html添加测试…...

Unity VR/MR开发-开发环境准备
视频讲解链接: 【XR马斯维】UnityVR/MR开发环境准备【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

matlab模糊控制实现路径规划
路径规划是机器人和自动驾驶系统中的重要问题之一,它涉及确定如何在给定环境中找到最优路径以达到特定目标。模糊控制是一种有效的控制方法,可以应用于路径规划问题。 路径规划算法的目标是在避免障碍物的情况下,找到机器人或车辆从起点到终…...

2025-06-02-IP 地址规划及案例分析
IP 地址规划及案例分析 参考资料 Plan for IP addressing - Cloud Adoption Frameworkwww.cnblogs.comimage-hosting/articles at master jonsam-ng/image-hosting 概述 在网络通信中,MAC 地址与 IP 地址分别位于 OSI 模型的数据链路层和网络层,二者协…...
