实数的奥秘:柯西序列深度解析
实数的奥秘:柯西序列深度解析
- 一、柯西序列的概念与性质
- 二、柯西序列定义无理数
- 三、柯西序列定义实数系统
实数,是初中学到的概念,我知都知道它是有理数和无理数的统称。

然而,实数可不只是小数点后的一堆零碎儿,它背后还有着高深莫测理论。
一、柯西序列的概念与性质
柯西序列(Cauchy sequence)是这样一个序列:随你任意给出一个正有理数ε,无论多小都行。总能在序列中找到这么一项,在这项之后任意两个元素,其差的绝对值都小于ε。
最简单的柯西序列就是常数序列,比如{3, 3 , 3, …},其所有元素的差值都为0,绝对小于任何的正有理数。
但是,这种小儿科的玩艺不是柯西序列的真正用武之地,它主要用于序列元素不同的情况。这时候柯西序列就会表现出一个特别的性质:随着序列项数的增加,元素间的差值越来越小。
如果把这种柯西序列中的元素看成数轴上的一系列点,那么越往右,这些点越密集(点与点间的距离越小)。但无论怎样密集,它们都位于某一个点的左侧。
如果把序列项数n做为横坐标,把序列元素的值$X_n作为纵坐标,则柯西序列就是下图中的一些点:

现在,相信你已经明白柯西序列是个什么东东了。这时候,咱们再用一种高大上的方法表示一下这玩艺。
数学定义:
设序列 { x n } ⊂ X \{x_n\}\subset X {xn}⊂X,若 { x n } \{x_n\} {xn}满足:当 m , n → ∞ m, n \to \infty m,n→∞时,有 d ( x m , x n ) → 0 d(x_m, x_n)\to 0 d(xm,xn)→0,则称 { x n } \{x_n\} {xn}是 X X X的柯西序列。
d ( x m , x n ) d(x_m, x_n) d(xm,xn)表示序列中的元素 x m x_m xm与 x n x_n xn的差的绝对值。
现在是不是看着也挺好理解的?这就是数学公式的特点。如果上来就摆公式,肯定头大,但是如果先理解了再去看,这玩艺就是纸老虎。
再看看它的性质:若序列 { x n } \{x_n\} {xn}收敛,则 { x n } \{x_n\} {xn}是柯西序列。
证明:
若序列 { x n } \{x_n\} {xn}收敛,则说明其有极限。
设 lim n → ∞ x n = x \lim_{n \to \infty} x_n = x limn→∞xn=x,则当 m , n → ∞ m, n \to \infty m,n→∞时,有 d ( x m , x n ) ≤ d ( x m , x ) + d ( x n , x ) → 0 d(x_m, x_n)\le d(x_m, x) + d(x_n, x)\to 0 d(xm,xn)≤d(xm,x)+d(xn,x)→0,故 { x n } \{x_n\} {xn}是柯西序列。
这个貌似也挺好理解的吧?
二、柯西序列定义无理数
举个最简单的元素不同的柯西序列例子,咱们都背过 π \pi π,假设有这么一个数列 {3, 3.1, 3.14, 3.141, 3.1415, …},也就是每个元素都在上一个元素的基础上增加1位小数。显然,越往后序列中元素的差值就越小。因为这个数是无限的,其差值无限趋近于0,而序列中的元素无限趋近于 π \pi π。
无限趋近于,这说的不就是极限吗?
表现在数轴上,它们就是一些越往右越集中的点,且这些点都位于 π \pi π的左侧,无限地接近 π \pi π这个点。
见证奇迹的时刻到了!尽管这个序列中的所有项都是有理数,但它们却可以收敛到一个无理数。柯西序列展示出了有理数与无理数之间的联系:无理数是有理数构成的柯西序列的极限。
如果把某个无理数(比如 π \pi π)看成空间中的一点,那么柯西序列就像射向这个点的一串子弹。只不过,这些子弹只能无限地接近于目标点,却永远别想打到它。
目标神秘人物:小子,别想打到我!
有理君:神了,我去!近在咫尺,咋就打不到呢?
目标神秘人物:因为我有不讲“理”的防护罩,而你的子弹讲“理”。
也就是说,这个有理数虽然无限地逼近无理数,但只要还在有理数的范围内,这就永远没有极限。

要想到达这个极限,必须突破有理数的范围。
突破有理数的条件就是有理数子弹是无穷无尽的,量变引起质变,就会达到极限,这个极限就是无理数。
这样,无理数就有了新的定义:有理数柯西序列的极限(序列元素不同)。
三、柯西序列定义实数系统
有了柯西序列的加持,我们可以给实数重新下个统一性的定义。
为什么要重新下个定义呢?因为“有理数和无理数的统称”这个定义没有揭示实数的实质。这种定义方法就好像把人定义为“男人和女人的统称”一样。
将人定义为男人和女人的统称虽然也没什么问题,但没有指出人和其他动物的区别。同样的道理,将实数定义为有理数和无理数的统称,也没说出实数与其他数的区别。
这个统一性的定义,官方有一个非常绕舌的学术表述:实数为所有收敛到同一极限的有理数序列的等价类。
这个定义可能比较严谨,但是不容易理解。尤其里面搞出个新名词:等价类。如果想了解这是什么玩艺,老金在文章最后会给出解释。
老金认为可以这样简单理解:实数是有理数柯西序列的极限。
一共不就这么两种情况嘛:
①有理数:柯西序列是个常数序列,就像{3, 3 , 3, …},这时候它的极限就是有理数。
②无理数:柯西序列中的元素值是不同的,就像{3, 3.1, 3.14, 3.141, 3.1415, …},这时候它的极限就是无理数。
就这么简单。
然而,这个定义丧失了“有理数和无理数的统称”的肤浅,有着深刻的意义:将有理数作为载体,以柯西序列为桥梁,用有理数表示无理数、实数,揭示出有理数、无理数、实数的联系。
最重要的,它还揭示了实物的根本性质:完备性。
所谓的完备性用一句话来形容就是“所有的……都……”。用柯西序列定义实数,实数的完备性就体现出来了:所有柯西序列都有极限。实数的完备性表现在数轴上,是我们学校里都学过的,就是所有的实数在数轴上都有对应的点、所有数轴上的点都对应一个实数。
附:“等价类”的解释
最后说说前面官方定义中的“等价类”是个啥。这玩艺其实说的是同一个极限可能对应多个不同的柯西序列,而因为它们的极限相同,这些不同的柯西序列其实是等价的。
还是拿 π \pi π举例子,它可以有多个柯西序列表示,除了前面说的{3, 3.1, 3.14, 3.141, 3.1415, …},还可以表示为:
{9257, 9257, 9257, 9257, 3, 3.1, 3.14, 3.141, 3.1415, …}
{5566, 9257, 5566, 9257, 3.2, 3.14, 3.141, 3.1415, …}
相信你已看明白老金想表达的意思,这样的柯西序列可以列出无数个,但它们的极限都是 π \pi π,因而都是等价的,这就是等价类的含义。
也就是说,如果存在多个柯西序列收敛到同一个极限,则将它们视为同一个实数。
但老金觉得这玩艺就是“严谨的复杂”,了不了解无伤大雅,所以才以附注的形式放在最后。谁还不明白这个意思呢?说白了就是这么点勾当:柯西序列的极限只跟最右侧的密集区有关,跟左侧那些元素的值根本没有任何关系。左边那些东东就是在那里摆造型,就像秃头上剩下的几根毛,聊胜于无。
相关文章:

实数的奥秘:柯西序列深度解析
实数的奥秘:柯西序列深度解析 一、柯西序列的概念与性质二、柯西序列定义无理数三、柯西序列定义实数系统 实数,是初中学到的概念,我知都知道它是有理数和无理数的统称。 然而,实数可不只是小数点后的一堆零碎儿,它背后…...

信息系统管理师试题-人力资源
信息系统管理师试题-人力资源 当组织计划的人力资源需求超过供给时,可通过下列方法解决,其中不包括() A降低录用标准,招聘新员工 B增加临时性员工和使用退休员工 C减少加班数量或工作时间 D提高员工工作效率 答案C 下…...

补偿电阻对ota零极点的影响
本文内容主要是关于补偿电阻对零极点产生的影响。 1.极点分析 该补偿电阻并不会影响在输出端的主极点,受影响的主要是镜像极点。 这里我们可以先单看电流镜部分,这个补偿电阻的作用在于将极点推向原来的两倍,从而达到增加带宽的目的[1]。 …...

UVM: uvm_sequence
topcic sequence overview sequence excution flow sequence class callbacks sequencer driver communication...
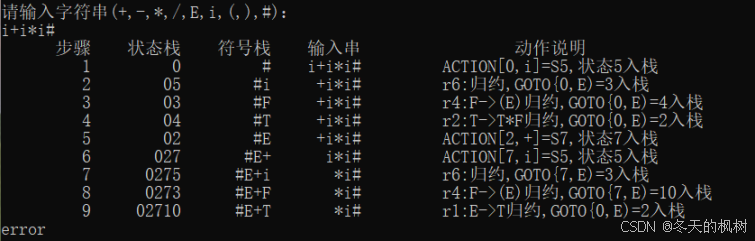
编译技术实验三之编译器的构造和设计
一、实验目的: 我们将设计多个不同的综合实验项目提供给学生选择。(如:LL(1)文法自动生成语法分析程序的设计;单词的自动识别与智能纠错;语言的程序编辑器;数学计算式的识别等)学生可在这些项目中选择1个项…...

数据挖掘——数据预处理
数据挖掘——数据预处理 数据预处理数据预处理 ——主要任务数据清洗如何处理丢失的数据如何处理噪声数据如何处理不一致数据 数据集成相关分析相关系数(也成为皮尔逊相关系数)协方差 数据规约降维法:PCA主成分分析降数据——抽样法数据压缩 数据预处理 数据预处理…...

ECharts饼图下钻
背景:项目上需要对Echarts饼图进行功能定制,实现点击颜色块,下钻显示下一层级占比说明:饼图实现点击下钻/面包屑返回的功能 数据结构 [{name: a,value: 1,children: [...]},... ]点击下钻 // 为图表绑定点击事件(需要…...

【RK3568笔记】Android修改开机动画
概述 Android 的开机动画是由一系列连续的 PNG 图片作为帧组成的动画形式,不是一张 GIF 图片。将各帧 PNG 图片以压缩方式进行保存(压缩方式要求是存储压缩),并将保存的文件名命名为 bootanimation.zip,这个 bootanim…...

嵌入式技术之Linux(Ubuntu) 一
一、Linux入门 1.硬件和操作系统以及用户的关系 一个传感器,获得数据后,需要向服务器发送数据。传感器传数据给上位机。 上位机需要一个程序来接收数据,那么这个上位机是什么机器? 我们的笔记本电脑就可以当成上位机。 两个手…...

代码随想录day39 动态规划7
打家劫舍 题目:198.打家劫舍 213.打家劫舍II 337.打家劫舍III 需要重做:全部 198.打家劫舍 思路:第i个房子偷与不偷,取决于第i-2个房子和第i-1个房子 注意:注意下标的一致性。现在的下标含义是房子的下标&#x…...
)
ESP32-S3模组上实现低功耗(5)
接前一篇文章:ESP32-S3模组上实现低功耗(4) 本文内容参考: 系统低功耗模式介绍 - ESP32-S3 - — ESP-IDF 编程指南 latest 文档 电源管理 - ESP32-S3 - — ESP-IDF 编程指南 latest 文档...

PDF转文本以及转图片:itextpdf
文章目录 🐒个人主页:信计2102罗铠威🏅JavaEE系列专栏📖前言:🎀 1. itextpdf1.1导入itextpdf的maven依赖1.2 提取文本代码1.3 pdf转换成图片代码(本地图片地址还是线上PDF的URL地址均支持&#…...

AnaConda下载PyTorch慢的解决办法
使用Conda下载比较慢,改为pip下载 复制下载链接到迅雷下载 激活虚拟环境,安装whl,即可安装成功 pip install D:\openai.wiki\ChatGLM2-6B\torch-2.4.1cu121-cp38-cp38-win_amd64.whl...

移动端自动化测试Appium-java
一、Appium的简介 移动端的自动化测试框架 模拟人的操作进行功能自动化常用于功能测试、兼容性测试 跨平台的自动化测试 二、Appium的原理 核心是web服务器,接受客户端的连接,接收客户端的命令,在手机设备上执行命令,收集命令…...

IO: 作业:Day1
思维导图 main.c #include"student.h" int main(int argc, const char *argv[]) { stuPtr hcreat(); int n0; add_node(h); add_node(h); add_node(h); show(h); save(h,"student.txt"); stuPtr ptrc…...

ue5 替换角色的骨骼网格体和动画蓝图
一开始动画蓝图,骨骼网格体都是用的女性角色 现在把它换成男性 编译 保存 运行 把动画类换成ABP_Manny 进入ABP_Manny中 进入到idle 找到这个拖进来 编译 就变成站着端枪 运行一下,没有问题...

el-cascader 树状选择-点击父级禁用子级
背景:项目上需要实现树状选择,点击父级禁用子级的功能,element组件本身没有该配置项说明:需要实现几个功能点:点击父级禁用子级;再次点击取消禁用;仅回填所选级;上下级不关联实现代码…...

AWS re:Invent 的创新技术
本月早些时候,Amazon 于 12 月 1 日至 5 日在内华达州拉斯维加斯举行了为期 5 天的 re:Invent 大会。如果您从未参加过 re:Invent 会议,那么最能描述它的词是“巨大”——不仅从与会者人数(60,000 人)来看&…...

PHP7和PHP8的最佳实践
php 7 和 php 8 的最佳实践包括:使用类型提示以避免运行时错误;利用命名空间组织代码并避免命名冲突;采用命名参数、联合类型等新特性增强可读性;用错误处理优雅地处理异常;关注性能优化,如避免全局变量和选…...
)
Debian、Ubuntu 22.04和ubuntu 24.04国内镜像源(包括 docker 源)
Debian 更换国内清华源 1、备份原文件mv /etc/apt/sources.list /etc/apt/sources.list.old 2、写入新源,以下是 Debian 11 的: cat > /etc/apt/sources.list << EOF deb https://mirrors.tuna.tsinghua.edu.cn/debian/ bullseye main contrib…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
