【17. 电话号码的字母组合 中等】
题目:
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例 1:
输入:digits = “23”
输出:[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]
示例 2:
输入:digits = “”
输出:[]
示例 3:
输入:digits = “2”
输出:[“a”,“b”,“c”]
提示:
- 0 <= digits.length <= 4
- digits[i] 是范围 [‘2’, ‘9’] 的一个数字。
思路:
数字和字母如何映射
首先要解决的问题是数字和字母如何映射,可以使用map或者定义一个二维数组,例如:string letterMap[10],来做映射,这里定义一个二维数组,代码如下:
// 数字和字母映射
const string letterMap[10] = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz" // 9
};
回溯法来解决n个for循环的问题
例如:输入:“23”,抽象为树形结构,如图所示:
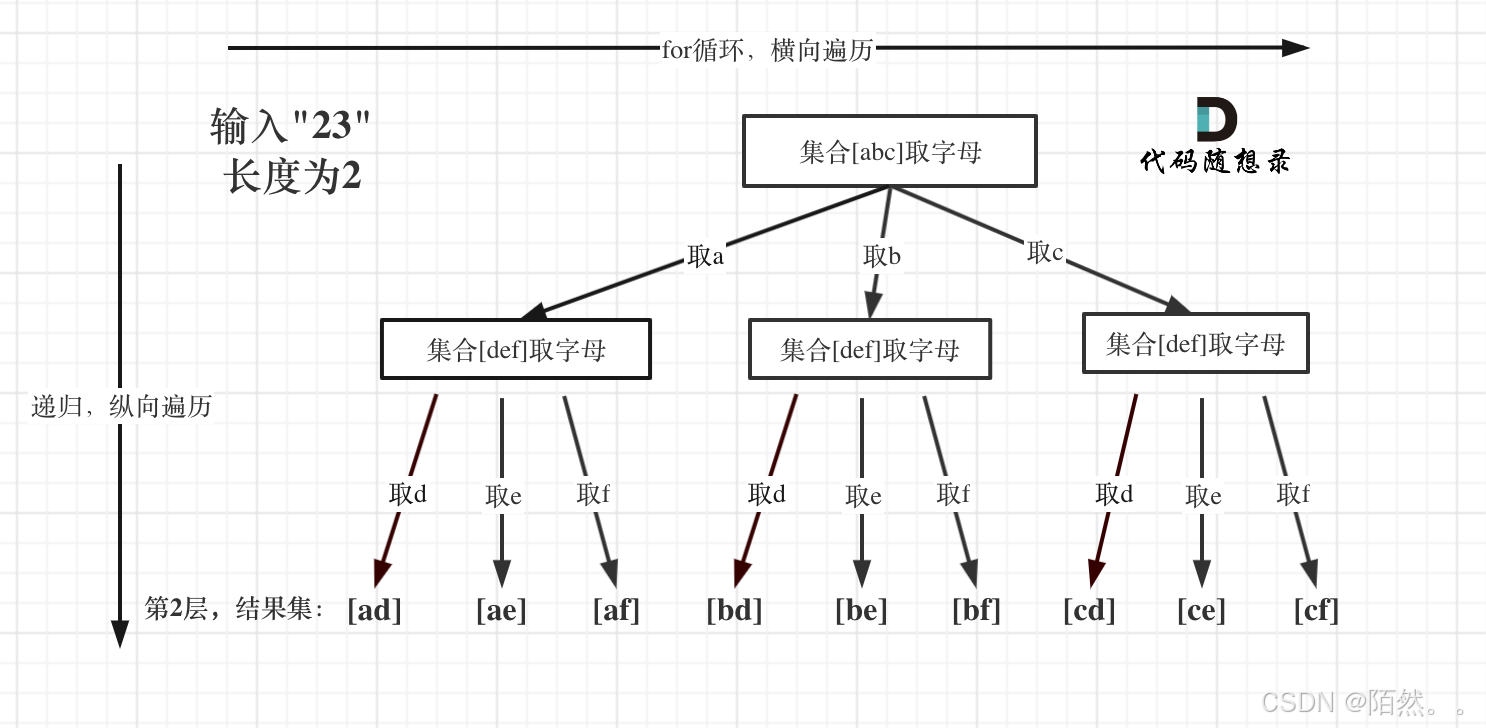
图中可以看出遍历的深度,就是输入"23"的长度,而叶子节点就是我们要收集的结果,输出[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”]。
回溯三部曲:
- 确定回溯函数参数
首先需要一个字符串path来收集叶子节点的结果,然后用一个字符串数组result保存起来,这两个变量我依然定义为全局。
再来看参数,参数指定是有题目中给的string digits,然后还要有一个参数就是int型的index。
注意这个index可不是77.组合 中等中的startIndex了。
这个index是记录遍历第几个数字了,就是用来遍历digits的(题目中给出数字字符串),同时index也表示树的深度。
代码如下:
vector<string> result;
string path;
void backtracking(const string& digits, int index)
- 确定终止条件
例如输入用例"23",两个数字,那么根节点往下递归两层就可以了,叶子节点就是要收集的结果集。
那么终止条件就是如果index 等于 输入的数字个数(digits.size)了(本来index就是用来遍历digits的)。
然后收集结果,结束本层递归。
代码如下:
if (index == digits.size()) {result.push_back(s);return;
}
- 确定单层遍历逻辑
首先要取index指向的数字,并找到对应的字符集(手机键盘的字符集)。
然后for循环来处理这个字符集,代码如下:
int digit = digits[index] - '0'; // 将index指向的数字转为int
string letters = letterMap[digit]; // 取数字对应的字符集
for(int i = 0; i < letters.size(); i++){path.push_back(letters[i]); // 处理backtracking(digits, index + 1); // 递归path.pop_back(); // 回溯
}
注意这里for循环,可不像是在回溯算法:求组合问题77.组合 中等中从startIndex开始遍历的。
因为本题每一个数字代表的是不同集合,也就是求不同集合之间的组合,而77.组合 中等是求同一个集合中的组合!
代码:
class Solution {
public:// 数字和字母映射const string letterMap[10] = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz" // 9};vector<string> result;string path;// charMap为当前数字对应的字母字符串void backtracking(const string& digits, int index){if(digits.size() == 0) return;if(index == digits.size()){result.push_back(path);return;}int digit = digits[index] - '0'; // 将index指向的数字转为intstring letters = letterMap[digit]; // 取数字对应的字符集for(int i = 0; i < letters.size(); i++){path.push_back(letters[i]); // 处理backtracking(digits, index + 1); // 递归path.pop_back(); // 回溯}}vector<string> letterCombinations(string digits) {backtracking(digits, 0);return result;}
};
总结:
时间复杂度: O(3^m * 4^n),其中 m 是对应三个字母的数字个数,n 是对应四个字母的数字个数
空间复杂度: O(3^m * 4^n)
本并重点强调了和前面讲解过的77.组合 中等的区别,本题是多个集合求组合,所以在回溯的搜索过程中,都有一些细节需要注意的。
参考:
代码随想录
相关文章:

【17. 电话号码的字母组合 中等】
题目: 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 示例 1: 输入:digits “23”…...
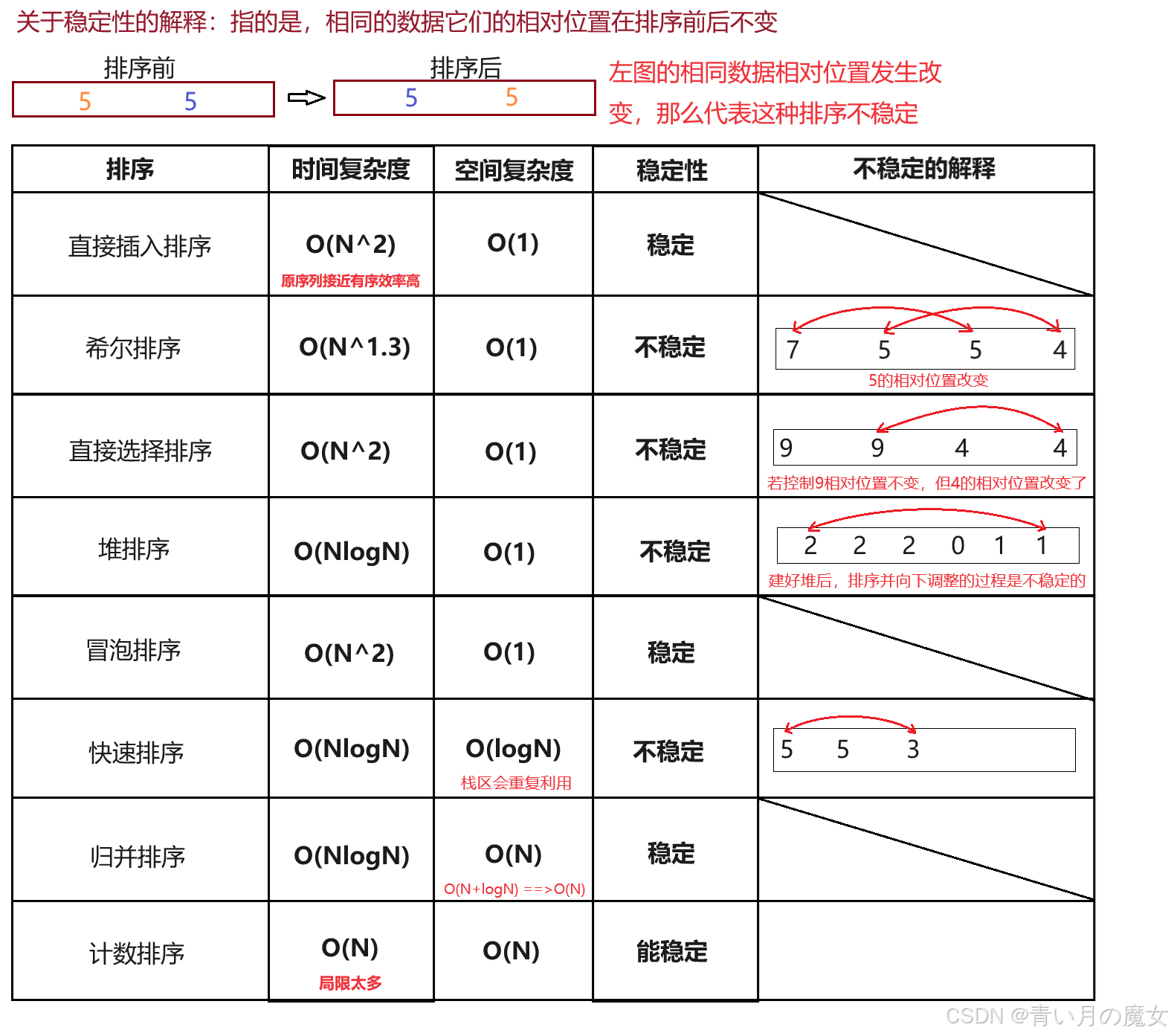
数据结构初阶---排序
一、排序相关概念与运用 1.排序相关概念 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的…...
【从0-1实现一个前端脚手架】
目录 介绍为什么需要脚手架?一个脚手架应该具备哪些功能? 脚手架实现初始化项目相关依赖实现脚手架 发布 介绍 为什么需要脚手架? 脚手架本质就是一个工具,作用是能够让使用者专注于写代码,它可以让我们只用一个命令…...
AI文章管理系统(自动生成图文分发到分站)
最近帮一个网上的朋友做了一套AI文章生成系统。他的需求是这样: 1、做一个服务端转接百度文心一言的生成文章的API接口。 2、服务端能注册用户,用户在服务端注册充值后可以获取一个令牌,这个令牌填写到客户端,客户端就可以根据客…...

【Leetcode 每日一题】3270. 求出数字答案
问题背景 给你三个 正 整数 n u m 1 num_1 num1, n u m 2 num_2 num2 和 n u m 3 num_3 num3。 数字 n u m 1 num_1 num1, n u m 2 num_2 num2 和 n u m 3 num_3 num3 的数字答案 k e y key key 是一个四位数,定义如下&…...
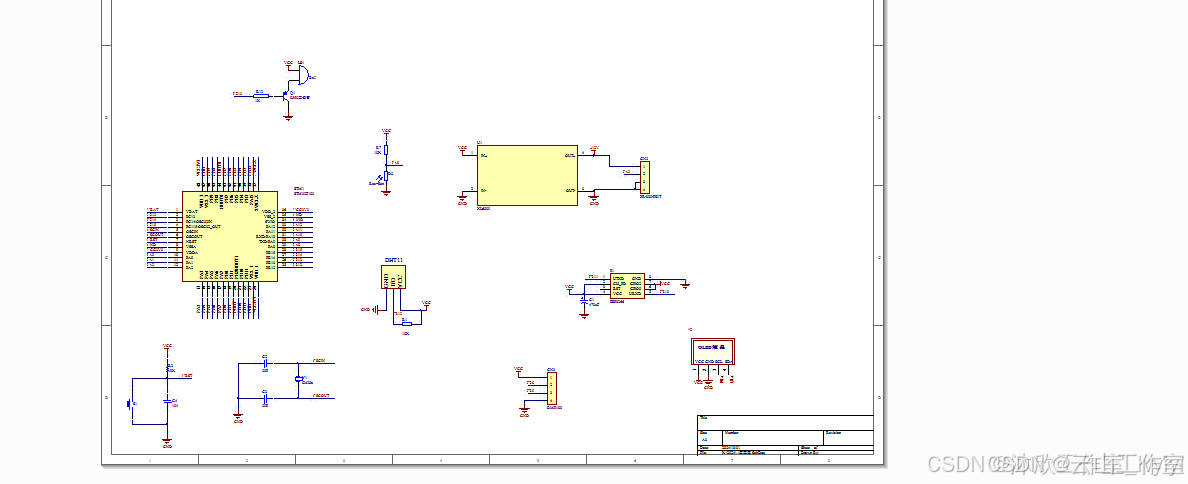
基于单片机的无线气象仪系统设计(论文+源码)
1系统方案设计 如图2.1所示为无线气象仪系统设计框架。系统设计采用STM32单片机作为主控制器,结合DHT11温湿度传感器、光敏传感器、BMP180气压传感器、PR-3000-FS-N01风速传感器实现气象环境的温度、湿度、光照、气压、风速等环境数据的检测,并通过OLED1…...

【数据库】Mysql精简回顾复习
一、概念 数据库(DB):数据存储的仓库数据库管理系统(DBMS):操纵和管理数据库的大型软件SQL:操作关系型数据库的编程语言,是一套标准关系型数据库(RDBMS)&…...

深入理解 HTTP 的 GET、POST 方法与 Request 和 Response
HTTP 协议是构建 Web 应用的基石,GET 和 POST 是其中最常用的请求方法。无论是前端开发、后端开发,还是接口测试,对它们的深入理解都显得尤为重要。在本文中,我们将介绍 GET 和 POST 方法,以及 Request 和 Response 的…...

MySQL 中联合索引相比单索引性能提升在哪?
首先我们要清楚所以也是要占用磁盘空间的,随着表中数据量越来越多,索引的空间也是随之提升的,因而单表不建议定义过多的索引,所以使用联合索引可以在一定程度上可以减少索引的空间占用其次,使用联合索引的情况下&#…...
第34天:安全开发-JavaEE应用反射机制攻击链类对象成员变量方法构造方法
时间轴: Java反射相关类图解: 反射: 1、什么是 Java 反射 参考: https://xz.aliyun.com/t/9117 Java 提供了一套反射 API ,该 API 由 Class 类与 java.lang.reflect 类库组成。 该类库包含了 Field 、 Me…...

C++笔记之数据单位与C语言变量类型和范围
C++笔记之数据单位与C语言变量类型和范围 code review! 文章目录 C++笔记之数据单位与C语言变量类型和范围一、数据单位1. 数据单位表:按单位的递增顺序排列2. 关于换算关系的说明3. 一般用法及注意事项4. 扩展内容5. 理解和使用建议二、C 语言变量类型和范围基本数据类型标准…...

算法-拆分数位后四位数字的最小和
力扣题目2160. 拆分数位后四位数字的最小和 - 力扣(LeetCode) 给你一个四位 正 整数 num 。请你使用 num 中的 数位 ,将 num 拆成两个新的整数 new1 和 new2 。new1 和 new2 中可以有 前导 0 ,且 num 中 所有 数位都必须使用。 …...

Python 管理 GitHub Secrets 和 Workflows
在现代软件开发中,自动化配置管理变得越来越重要。本文将介绍如何使用 Python 脚本来管理 GitHub 仓库的 Secrets 和 Workflows,这对于需要频繁更新配置或管理多个仓库的团队来说尤为有用。我们将分三个部分进行讨论:设置 GitHub 权限、创建 GitHub Secret 和创建 GitHub Wo…...

指令的修饰符
指令的修饰符 参考文献: Vue的快速上手 Vue指令上 Vue指令下 Vue指令的综合案例 文章目录 指令的修饰符指令修饰符 结语 博客主页: He guolin-CSDN博客 关注我一起学习,一起进步,一起探索编程的无限可能吧!让我们一起努力&…...

C# 正则表达式完全指南
C# 正则表达式完全指南 C#通过 System.Text.RegularExpressions 命名空间提供强大的正则表达式支持。本指南将详细介绍C#中正则表达式的使用方法、性能优化和最佳实践。 1. 基础知识 1.1 命名空间导入 using System.Text.RegularExpressions;1.2 基本使用 public class Re…...

【笔记整理】记录参加骁龙AIPC开发者技术沙龙的笔记
AIoT 首先了解了一个概念叫AIoT,我的理解就是AI IoT 5G,通过AI的发展使得边缘计算、数据整合和处理变得快捷方便,不仅限于传统的云端数据处理,在边缘的IoT设备上也可以进行智能化打造,通过5G的通信能力扩展可以实现…...

论文解析 | 基于语言模型的自主代理调查
论文 《A Survey on Large Language Model-based Autonomous Agents》 对基于大型语言模型(LLM)的自主智能体(Autonomous Agents)进行了全面调查。随着大型语言模型(如 GPT 系列、BERT、T5 等)的快速发展&a…...

面试加分项:Android Framework AMS 全面概述和知识要点
第一章:AMS 的架构与组件 1.1 AMS 整体架构 在 Android 系统的庞大体系中,AMS(Activity Manager Service)就如同一个中枢神经系统,是整个系统的核心服务之一,对应用的性能和用户体验有着直接且关键的影响 。它的整体架构由 Client 端和 Service 端两大部分组成,这两端相…...

EasyCVR视频汇聚平台如何配置webrtc播放地址?
EasyCVR安防监控视频系统采用先进的网络传输技术,支持高清视频的接入和传输,能够满足大规模、高并发的远程监控需求。平台支持多协议接入,能将接入到视频流转码为多格式进行分发,包括RTMP、RTSP、HTTP-FLV、WebSocket-FLV、HLS、W…...

用户界面软件04
后果 使用这种架构很容易对两个层面的非功能性需求进行优化,但是你仍然需要小心不要将功能 需求重复实现。 现在,两个层面可能有完全不同的设计。比如,用户界面层可能使用配件模型(Widget Model), 以大量的…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
