网络安全-安全散列函数，信息摘要SHA-1，MD5原理

安全散列函数

        单向散列函数或者安全散列函数之所以重要，不仅在于消息认证(消息摘要。数据指纹)。还有数字签名（加强版的消息认证）和验证数据的完整性。常见的单向散列函数有MD5和SHA

散列函数的要求

        散列函数的目的是文件、消息或者其它数据块产生“指纹”。为满足在消息认证中的应用，散列函数H必须具有下列性质：

        （1）H可适用于随意长度的数据块。

        （2）H能够生成固定长度的输出。

        （2）对于随意给定的x，计算H(x)相对easy，而且能够用软/硬件实现。

        （4）对于随意给定的h，找到满足H(x)=h的x在计算上不可行。满足这一特性的散列函数称之为：具备抗原像攻击性。

        （5）对于随意给定的数据块x，找到满足H(y)=H(x)的y ≠ x在计算上是不可行；满足这一特性的散列函数称之为：抗弱碰撞性。

        （6）找到满足H(x) = H(y)的随意一对(x,y)在计算上是不可行的。

满足这一特性的散列函数称之为：抗碰撞性。

        前三个性质是使用散列函数进行消息认证的实际可行要求。第四个属性，抗原像攻击，防止攻击者能够回复秘密值。抗弱碰撞性保证了对于给定的消息。不可能找到具有同样散列值的可替换消息。

        满足上面前5个性质的散列函数称之为弱散列函数。

假设还满足第6个性质则称之为强散列函数。

一般来说：能够认识散列函数的两个特点就OK，1.输出固定长度的 2. 不可逆转！

散列函数的安全性

        有两种方法能够攻击安全散列函数：password分析法和暴力攻击法。

散列函数抵抗暴力攻击的强度全然依赖于算法生成的散列码长度。

Van Oorschot和Wiener以前提出，花费1000万美元涉及一个被专门用来搜索MD5算法碰撞的机器，则平均24天内就能够找到一个碰撞。

        2004年8月中国password学家王小云教授等首次发布了提出一种寻找MD5碰撞的新方法。眼下利用该方法用普通微机几分钟内就可以找到MD5的碰撞。MD5已经呗彻底攻破。

简单散列函数

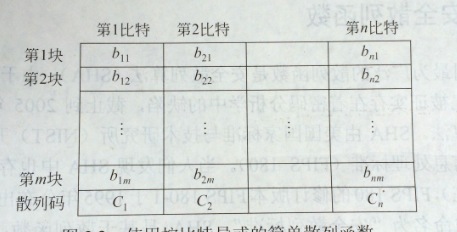
        全部的散列函数都依照以下的基本操作。把输入（消息、文件等）看成n比特块的序列。对输入用迭代方法处理一块，生成n比特的散列函数。

        一种最简单散列函数的每个数据块都依照比特异或。

例如以下所看到的

                Ci = bi1⊕ bi2⊕ … ⊕ bim

        当中：

                Ci为散列码的第i比特。1<=  i <=n;

                m为输入中n比特数据块的数目。

                bij为第j块的第i比特。

                ⊕为异或操作

        下图说明了这个操作：

上图仅仅是简单的散列函数。由于没一列都有同样的可能性。所以这个函数的有效性差。

SHA安全散列函数

        近些年，应用最广泛的散列函数是SHA。

由于其它每一种被广泛应用的散列函数都已经被证实存在这password分析学中的缺陷。接着到2005年，SHA也许仅存的安全散列算法。SHA由美国国家标准与技术研究院（NIST）开发。

● 1995年发布SHA-1
● 2002年，发布了SHA-2(SHA-256、SHA-384、SHA-512)
● 2008年，添加了SHA-224

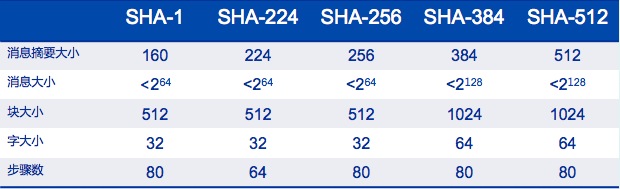
更具体的例如以下图所看到的：

以下对SHA-512做一下介绍，其它SHA算法与之非常类似。该算法以最大长度不超过2128比特作为输入，生成512比特的消息摘要输出。输入以1024比特的数据块进行处理。

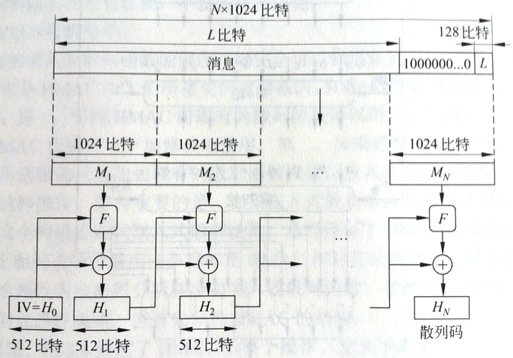
如图所看到的：

处理过程：

● 第1步、追加填充比特

填充消息使其长度模1024同余896[长度 896(模1024)]。及时消息已经是期望的长度，也总是要加入填充。填充部分是由单个比特1后接所需个数的比特0构成。

● 第2步、追加长度

将128比特的数据块追加在消息上。该数据被看作是128比特的无符号整数。它含有原始消息的长度。经过前两步，生成了1024倍数的消息。如上图所看到的。被延展的消息表示为1024比特的数据块M1，M2，M3...Mn。

结合这两点：“同余”比較难以理解，填充比特的逻辑能够这么理解：填充的目的是为了形成1024的倍数，可是，最后一个1024块的最后128比特必须保留（用于记录原始消息的长度）。举例：

原始消息895比特，那么须要填充1个比特。这样895+1+128=1024

原始消息896比特。这样的情况下，加上128字节正好是1024，可是依照规则，仍是要填充1024个字节。

原始消息897比特，897+128>1024，所以须要填充。填充1023个比特。

● 第3步、初始化散列缓冲区

用512比特的缓冲区保存散列函数中间和终于结果。缓冲区能够是8个64比特的寄存器（a,b,c,d,e,f,g,h），这些寄存器初始化为64比特的整数（十六进制）:

        a=6a09e667f3bcc908

        b=bb67ae8584caa73b

        c=3c6ef372fe94f82b

        d=a54ff53a5f1d36f1

        e=510e527fade682d1

        f=9b05688c2b3e6c1f

        g=1f83d9abfb41bd6b

        h=5be0cd19137e2179

这些值以逆序的形式存储，即字的最高字节存在最低地址（最左边）字节位置。

这些字的获取方式例如以下：前8个素数取平方跟，取小数部分前64位。

● 第4步、处理1024比特的数据块消息

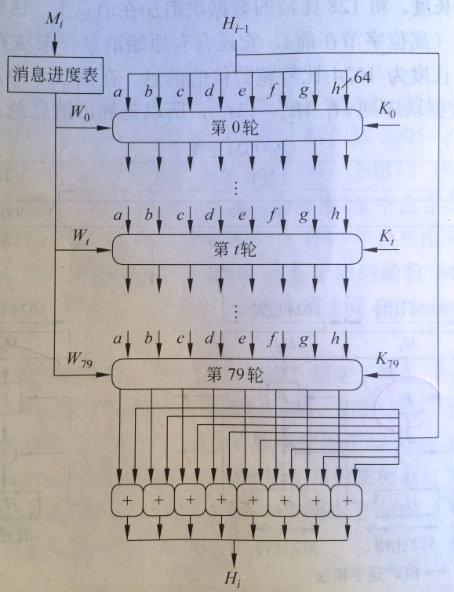
        算法的核心是80轮迭代构成的模块。

该模块在上图中标记为F，下图是其逻辑关系。每一轮都以512比特的缓冲区值abcdefgh作为输入。而且更新缓冲区内容。

在第一轮时，缓冲区的值是中间值Hi-1.在随意t轮。使用从当前正在处理的1024比特的数据块（Mi）导出64位比特值Wt。每一轮还使用附加常数Kt。当中0<=t<=79表示80轮中的某一轮。这些常数的获取方式例如以下：前8个素数的立方根。取小数部分的前64位。这些常数提供了64位随机串集合，能够初步消除输入数据中的不论什么规则性。第80轮输出加到第1轮输入（Hi-1）生成Hi。

缓冲区里的8个字与Hi-1中对应的字进行模264加法运算。

● 第5步、输出

当全部N个1024比特的数据块都处理完成后，从第N阶段输出的便是512比特的消息摘要。

        SHA-512算法使得散列码的随意比特都是输入端每1比特的函数。基本函数F的复杂迭代产生非常好的混淆效果；即随机取两组类似的消息也不可能生成同样的散列码。除非SHA-512隐含一些直到如今都还没有发布的弱点。