399. 除法求值【 力扣(LeetCode) 】
文章目录
- 零、LeetCode 原题
- 一、题目描述
- 二、测试用例
- 三、解题思路
- 3.1 图的路径搜索
- 3.2 路径压缩
- 四、参考代码
- 4.1 图的路径搜索
- 4.2 路径压缩
零、LeetCode 原题
399. 除法求值
一、题目描述
给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。
注意:输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
注意:未在等式列表中出现的变量是未定义的,因此无法确定它们的答案。
二、测试用例
示例 1:
输入:equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出:[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释:
条件:a / b = 2.0, b / c = 3.0
问题:a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果:[6.0, 0.5, -1.0, 1.0, -1.0 ]
注意:x 是未定义的 => -1.0
示例 2:
输入:equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
输出:[3.75000,0.40000,5.00000,0.20000]
示例 3:
输入:equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
输出:[0.50000,2.00000,-1.00000,-1.00000]
提示:
1 <= equations.length <= 20
equations[i].length == 2
1 <= Ai.length, Bi.length <= 5
values.length == equations.length
0.0 < values[i] <= 20.0
1 <= queries.length <= 20
queries[i].length == 2
1 <= Cj.length, Dj.length <= 5
Ai, Bi, Cj, Dj 由小写英文字母与数字组成
三、解题思路
3.1 图的路径搜索
- 基本思路:
如果将每个 equations 看作 边 ,value 看作 边权,则 queries 相当于查询某条路径的权重和。 - 具体思路:
- 构建有向图
- 路径搜索
- 如果顶点不存在,则存入 -1 ;
- 如果顶点相同,则存入 1;
- 使用深度搜索进行路径搜索,查找该路径并计算权重累加和。
3.2 路径压缩
- 基本思路:
就在上一个方法的基础上,进行路径压缩即可。每搜索完一个,将结果保存。 - 具体思路:
同上,在最后一步搜索完路径时,保存结果,可以作为下次搜索使用。
四、参考代码
4.1 图的路径搜索
时间复杂度: O ( k ∣ E ∣ ) \Omicron(k|E|) O(k∣E∣)【查找 k 条路径,每条路径最坏情况就是遍历所有的边】
空间复杂度: O ( ∣ E ∣ ) \Omicron(|E|) O(∣E∣)【使用空间有:图的边,图的顶点(最坏2倍边的空间),递归深度(最坏遍历所有边),已搜索顶点集合(最坏搜索过所有顶点)】
class Solution {
public:unordered_map<string, unordered_map<string, double>> m;double dfs(string now, string obj, unordered_set<string>& used) {if (m.count(now) == 0)return 0;if (m[now].count(obj))return m[now][obj];for (const auto& next : m[now]) {if (used.count(next.first))continue;used.emplace(next.first);auto ans = dfs(next.first, obj, used);if (ans)return ans * next.second;}return 0;}vector<double> calcEquation(vector<vector<string>>& equations,vector<double>& values,vector<vector<string>>& queries) {vector<double> ans;for (int i = 0; i < equations.size(); i++) {m[equations[i][0]].emplace(equations[i][1], values[i]);m[equations[i][1]].emplace(equations[i][0], 1 / values[i]);}for (int i = 0; i < queries.size(); i++) {if (m.count(queries[i][0]) == 0 || m.count(queries[i][1]) == 0) {ans.emplace_back(-1.0);} else if (queries[i][0] == queries[i][1]) {ans.emplace_back(1.0);} else {unordered_set<string> used;ans.emplace_back(dfs(queries[i][0], queries[i][1], used));if (ans.back() == 0.0)ans.back() = -1.0;}}return ans;}
};
4.2 路径压缩
时间复杂度: O ( k α ( ∣ E ∣ ) ) \Omicron(k\alpha(|E|)) O(kα(∣E∣))【 α ( n ) \alpha(n) α(n) 是一个增长很慢的函数,其值都不超过 4】
空间复杂度: O ( ∣ E ∣ ) \Omicron(|E|) O(∣E∣)
class Solution {
public:unordered_map<string, unordered_map<string, double>> m;double dfs(string now, string obj, unordered_set<string>& used) {if (m.count(now) == 0)return 0;if (m[now].count(obj))return m[now][obj];for (const auto& next : m[now]) {if (used.count(next.first))continue;used.emplace(next.first);auto ans = dfs(next.first, obj, used);if (ans)return ans * next.second;}return 0;}vector<double> calcEquation(vector<vector<string>>& equations,vector<double>& values,vector<vector<string>>& queries) {vector<double> ans;for (int i = 0; i < equations.size(); i++) {m[equations[i][0]].emplace(equations[i][1], values[i]);m[equations[i][1]].emplace(equations[i][0], 1 / values[i]);}for (int i = 0; i < queries.size(); i++) {if (m.count(queries[i][0]) == 0 || m.count(queries[i][1]) == 0) {ans.emplace_back(-1.0);} else if (queries[i][0] == queries[i][1]) {ans.emplace_back(1.0);} else {unordered_set<string> used;ans.emplace_back(dfs(queries[i][0], queries[i][1], used));if (ans.back() == 0.0)ans.back() = -1.0;else{ // 保存结果m[queries[i][0]].emplace(queries[i][1],ans.back()); m[queries[i][1]].emplace(queries[i][0],1/ans.back()); }}}return ans;}
};
相关文章:
 】)
399. 除法求值【 力扣(LeetCode) 】
文章目录 零、LeetCode 原题一、题目描述二、测试用例三、解题思路3.1 图的路径搜索3.2 路径压缩 四、参考代码4.1 图的路径搜索4.2 路径压缩 零、LeetCode 原题 399. 除法求值 一、题目描述 给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,…...

算法日记1:洛谷p2678跳石头(二分答案)
1、题目 二、题解: 2.1解题思路: 1.题目要求求出最小值最大,明显的二分答案题目,所以我们可以二分可以跳跃距离int l-1,rL1; 2.此时我们思考lmid和rmid的处理,当我们的check(mid)为true时候 表明我们此时的mid是符合要求的, 那么…...

Unity shader中真的可以动态关闭Stencil Test吗?
这个问题很多年前就有人问了: https://discussions.unity.com/t/how-to-disable-the-stencil-block-via-shader-properties/600273/1 最后的答案是: set [_StencilComp] to CompareFunction.Disabled to disable the Stencil Op completely. 但是我测试…...

YOLOv9改进,YOLOv9自研检测头融合HyCTAS的Self_Attention自注意力机制,2024,适合目标检测、分割任务
摘要 论文提出了一种新的搜索框架,名为 HyCTAS,用于在给定任务中自动搜索高效的神经网络架构。HyCTAS框架结合了高分辨率表示和自注意力机制,通过多目标优化搜索,找到了一种在性能和计算效率之间的平衡。 # 理论介绍 自注意力(Self-Attention)机制是HyCTAS框架中的一个…...

计算机网络 (36)TCP可靠传输的实现
前言 TCP(传输控制协议)是一种面向连接的、可靠的、基于字节流的传输层通信协议。TCP通过多种机制实现可靠传输,这些机制主要包括连接管理、序列号和确认应答机制、重传机制、流量控制、拥塞控制等。 一、连接管理 TCP使用三次握手࿰…...

Git版本控制 - 创建使用Repository
Git版本控制 – 创建使用Repository Version Control with Git - Create and Use Repository By JacksonML 上文提到,Git是一种分布式版本控制系统。作为全球范围内广泛使用的工具,如何将项目分步骤运用到其中呢? 本文简要介绍如何用Git工…...

MySQL —— 在CentOS9下安装MySQL
MySQL —— 在CentOS9下安装MySQL 1.查看自己操作系统的版本2.找到对应的安装源3.上传我们在windows下,下载的文件,解压4.执行rpm命令,启用MySQL8仓库5.执行dnf install -y mysql-community-server6.设置开机自启动7.获得初始密码8.登录MySQL…...

LeetCode 热题 100_腐烂的橘子(52_994_中等_C++)(图;广度优先遍历(队列))
LeetCode 热题 100_腐烂的橘子(52_994) 题目描述:输入输出样例:题解:解题思路:思路一(广度优先遍历(队列)): 代码实现代码实现(思路一…...

Nginx 可观测性最佳实践
Nginx 介绍 Nginx 是一个开源、轻量级、高性能的 HTTP 和反向代理服务器,也可以用于 IMAP/POP3 代理服务器。Nginx 因其采用的异步非阻塞工作模型,使其具备高并发、低资源消耗的特性。高度模块化设计也使得 Nginx 具备很好的扩展性,在处理静…...

LabVIEW光流跟踪算法
1. 光流跟踪算法的概述 光流(Optical Flow)是一种图像处理技术,用于估算图像中像素点的运动。通过比较连续帧图像,光流算法可以分析图像中的运动信息,广泛用于目标跟踪、运动检测和视频处理等场景。该示例使用了NI Vi…...

Jira用例自动去除summary重复用例
title: Jira用例自动去除summary重复用例 tags: - jira - python categories: - python一、背景与需求二、解决方案思路三、实施步骤本文永久更新地址: 在使用 Jira 进行项目管理时,测试用例的维护至关重要。随着项目推进,用例数量增多,可能…...

基于openEuler22.03SP4部署Prometheus+Grafana
测试环境 Virtual Box,openEuler-22.03-LTS-SP4-x86_64-dvd.iso,4 vCPU, 8G RAM, 60 vDisk。最小化安装。需联网。 系统环境 关闭防火墙 systemctl stop firewalld systemctl disable firewalld systemctl status firewalld selinux关闭 sed -ri…...

泛目录和泛站有什么差别
啥是 SEO 泛目录? 咱先来说说 SEO 泛目录是啥。想象一下,你有一个巨大的图书馆,里面的书架上摆满了各种各样的书,每一本书都代表着一个网页。而 SEO 泛目录呢,就像是一个超级图书管理员,它的任务就是把这些…...
)
css 布局及动画应用(flex+transform+transition+animation)
文章目录 css 布局及动画应用animationtransform,transition,animation 综合应用实例代码实例解释 css 布局及动画应用 Display用法 作用:用于控制元素的显示类型,如块级元素、内联元素、无显示等。常见属性值及示例:…...

springboot vue uniapp 仿小红书 1:1 还原 (含源码演示)
线上预览: 移动端 http://8.146.211.120:8081/ 管理端 http://8.146.211.120:8088/ 小红书凭借优秀的产品体验 和超高人气 目前成为笔记类产品佼佼者 此项目将详细介绍如何使用Vue.js和Spring Boot 集合uniapp 开发一个仿小红书应用,凭借uniapp 可以在h5 小程序 app…...

lombok在高版本idea中注解不生效的解决
环境: IntelliJ IDEA 2024.3.1.1 Spring Boot Maven 问题描述 使用AllArgsConstructor注解一个用户类,然后调用全参构造方法创建对象,出现错误: java: 无法将类 com.itheima.pojo.User中的构造器 User应用到给定类型; 需要:…...

跨境电商领域云手机之选:亚矩阵云手机的卓越优势
在跨境电商蓬勃发展的当下,云手机已成为众多企业拓展海外市场的得力助手。亚矩阵云手机凭借其独特优势,在竞争激烈的云手机市场中崭露头角。不过,鉴于市场上云手机服务供应商繁多,企业在抉择时需对诸多要素予以审慎考量。 跨境电商…...

Linux第二课:LinuxC高级 学习记录day02
2.4、shell中的特殊字符 2.4.4、命令置换符 或者 $() 反引号:esc下面的按键,英文状态下直接按 功能:将一个命令的输出作为另一个命令的参数 echo 不会认为hostname是一个命令 加上 之后,先执行hostname,拿到主机名…...
)
6. NLP自然语言处理(Natural Language Processing)
自然语言是指人类日常使用的语言,如中文、英语、法语等。 自然语言处理是人工智能(AI)领域中的一个重要分支,它结合了计算机科学、语言学和统计学的方法,通过算法对文本和语音进行分析,使计算机能够理解、解…...
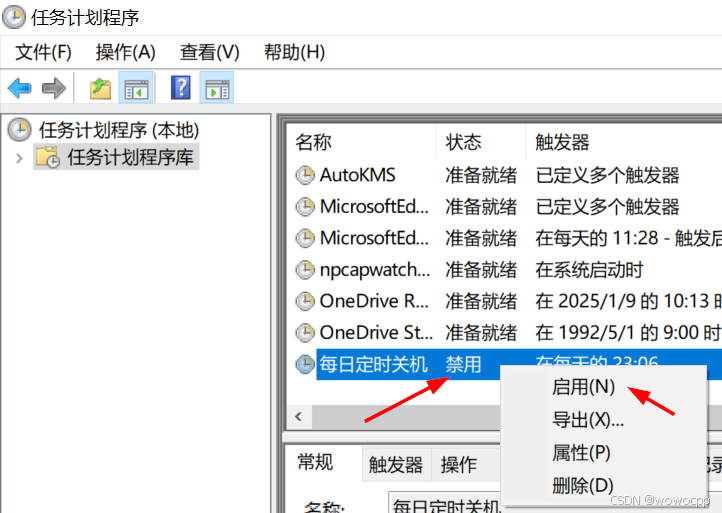
win10电脑 定时关机
win10电脑 定时关机 https://weibo.com/ttarticle/p/show?id2309405110707766296723 二、使用任务计划程序设置定时关机打开任务计划程序: 按下“Win S”组合键,打开搜索框。 在搜索框中输入“任务计划程序”,然后点击搜索结果中的“任务…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
