基于考研概率论知识解读 Transformer:为何自注意力机制要除以根号 dk
Transformer自注意力机制中除以 d k \sqrt{d_k} dk深度剖析
【 Transformer 系列,故事从 d k \sqrt{d_k} dk说起】
LLM这么火,Transformer厥功甚伟,某天心血来潮~,再去看看!
它长这个样子: 深入浅出 Transformer
看完后,想起了老生常谈 d k \sqrt{d_k} dk问题,必须一探究竟:Transformer 中缩放点积注意力机制探讨:除以根号 dk 理由及其影响
感觉不够清楚,还是再Review下考研概率论,有了:基于考研概率论知识解读 Transformer:为何自注意力机制要除以根号 dk,中间会涉及初始化、标准化、Sofrmax函数,于是继续
【初始化相关】:深度学习中的常见初始化方法:原理、应用与比较
【标准化系列】: 数据为什么要进行标准化:Z-标准化的神奇蜕变,带出了关联知识点: 深度 “炼丹” 术之 Batch Normalization 与 Z - 标准化:开启数据的神秘转换
【Softmax复习】:Softmax 层反向传播梯度计算实例解析,中间想到了经常配套使用的交叉熵,于是梳理了交叉熵的前世今生KL 散度:多维度解读概率分布间的隐秘 “距离”
熵与交叉熵:从不确定性角度理解 KL 散度
机器学习、深度学习关于熵你所需要知道的一切
摘要
本文深入探讨了Transformer自注意力机制中除以 d k \sqrt{d_k} dk这一关键操作的原因。通过详细的推导过程揭示 d k \sqrt{d_k} dk的来源,并结合Softmax函数的特性,分析不除以 d k \sqrt{d_k} dk以及除以结果偏离 d k \sqrt{d_k} dk时对模型造成的后果及其内在原因,旨在为理解Transformer的工作原理提供全面且深入的视角。
引言
Transformer架构在自然语言处理及其他诸多领域取得了巨大成功,其自注意力机制是核心创新点之一。在自注意力机制的计算过程中,除以 d k \sqrt{d_k} dk(其中 d k d_k dk是键(Key)向量的维度)这一操作对模型的稳定性和性能起着至关重要的作用,本文结合考研中的概率知识对除以 d k \sqrt{d_k} dk进行理解。
一、考研概率论内容复习
在Transformer自注意力机制中关于方差推导主要用到了以下考研概率知识:

- 期望与方差的基本定义及性质
- 期望:期望 E ( X ) E(X) E(X) 表示随机变量 X X X 取值的平均水平。
- 方差:方差 V a r ( X ) = E [ ( X − E ( X ) ) 2 ] = E [ X 2 ] − ( E [ X ] ) 2 Var(X)=E[(X - E(X))^2]=E[X^2]-(E[X])^2 Var(X)=E[(X−E(X))2]=E[X2]−(E[X])2,用于衡量随机变量取值的离散程度。
- 独立随机变量的性质
- 若 X X X 和 Y Y Y 是两个独立的随机变量,则 E [ X Y ] = E [ X ] E [ Y ] E[XY]=E[X]E[Y] E[XY]=E[X]E[Y] 。
- 对于独立随机变量 X X X 和 Y Y Y, V a r ( X Y ) = E [ X 2 ] E [ Y 2 ] − ( E [ X ] E [ Y ] ) 2 Var(XY)=E[X^2]E[Y^2]-(E[X]E[Y])^2 Var(XY)=E[X2]E[Y2]−(E[X]E[Y])2 。
- 若 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn 相互独立,那么 V a r ( ∑ i = 1 n X i ) = ∑ i = 1 n V a r ( X i ) Var(\sum_{i = 1}^{n}X_i)=\sum_{i = 1}^{n}Var(X_i) Var(∑i=1nXi)=∑i=1nVar(Xi) 。
- 随机变量的分布
假设随机变量 q i q_i qi 和 k i k_i ki 独立同分布,简化了分析过程,使得可以基于相同的分布特性对所有变量进行统一处理。
二、选择除以 d k \sqrt{d_k} dk的原因
1. 稳定方差
在自注意力机制中,计算注意力分数时涉及查询(Query)向量与键(Key)向量的点积。假设Query向量 Q Q Q和Key向量 K K K的元素是独立同分布的随机变量,均值为0,方差为1(实际模型参数随机初始化时接近此假设)。对于长度为 d k d_k dk的向量 Q = ( q 1 , q 2 , ⋯ , q d k ) Q=(q_1,q_2,\cdots,q_{d_k}) Q=(q1,q2,⋯,qdk)和 K = ( k 1 , k 2 , ⋯ , k d k ) K=(k_1,k_2,\cdots,k_{d_k}) K=(k1,k2,⋯,kdk),它们的点积 S = ∑ i = 1 d k q i k i S = \sum_{i = 1}^{d_k}q_ik_i S=i=1∑dkqiki
根据方差性质, V a r ( S ) = ∑ i = 1 d k V a r ( q i k i ) Var(S)=\sum_{i = 1}^{d_k}Var(q_ik_i) Var(S)=i=1∑dkVar(qiki)由于 q i q_i qi和 k i k_i ki相互独立, V a r ( q i k i ) = E [ q i 2 ] E [ k i 2 ] − ( E [ q i ] E [ q i ] ) 2 Var(q_ik_i)=E[q_i^2]E[k_i^2]-(E[q_i]E[q_i])^2 Var(qiki)=E[qi2]E[ki2]−(E[qi]E[qi])2已知 E [ q i ] = E [ k i ] = 0 E[q_i]=E[k_i]=0 E[qi]=E[ki]=0, V a r ( q i ) = V a r ( k i ) = 1 Var(q_i)=Var(k_i)=1 Var(qi)=Var(ki)=1,则 E [ q i 2 ] = E [ k i 2 ] = 1 E[q_i^2]=E[k_i^2]=1 E[qi2]=E[ki2]=1,所以 V a r ( q i k i ) = 1 Var(q_ik_i)=1 Var(qiki)=1,进而 V a r ( S ) = d k Var(S)=d_k Var(S)=dk
这表明点积 S S S的方差随维度 d k d_k dk增大而线性增大。为使点积结果方差稳定,除以 d k \sqrt{d_k} dk,即新变量 S ′ = S d k S'=\frac{S}{\sqrt{d_k}} S′=dkS的方差 V a r ( S ′ ) = 1 d k V a r ( S ) = 1 Var(S') = \frac{1}{d_k}Var(S)=1 Var(S′)=dk1Var(S)=1稳定的方差有助于后续Softmax函数输入处于合理范围,避免其输出概率分布过于极端,保证模型训练稳定性。
2. 平衡维度影响
除以 d k \sqrt{d_k} dk可视为一种归一化操作,有助于平衡不同维度特征在注意力计算中的贡献。若不进行此缩放,高维度向量在点积运算中可能占据主导,使模型过度关注某些维度信息,忽略其他维度。通过除以 d k \sqrt{d_k} dk,不同维度影响更均衡,模型能全面考虑序列元素关系。
三、 d k \sqrt{d_k} dk的来源推导
如前文所述,基于随机向量点积方差分析。设 Q Q Q和 K K K向量元素为独立同分布随机变量,均值为0,方差为1。点积 S = ∑ i = 1 d k q i k i S = \sum_{i = 1}^{d_k}q_ik_i S=i=1∑dkqiki,其方差 V a r ( S ) = d k Var(S)=d_k Var(S)=dk。
为将点积结果方差稳定在1附近,需对其归一化。自然的想法是除以与方差相关量,即除以 V a r ( S ) \sqrt{Var(S)} Var(S),也就是 d k \sqrt{d_k} dk。这样处理后,点积结果的方差得以稳定,为后续Softmax函数提供合适输入。
四、不恰当缩放的后果
1. 不除以 d k \sqrt{d_k} dk
若不除以 d k \sqrt{d_k} dk,随着 d k d_k dk增大,点积结果方差增大。输入到Softmax函数的数值方差过大,会使Softmax输出概率分布极其不均匀,大部分概率集中在少数较大数值对应元素上。
在反向传播中,这种不均匀分布导致梯度问题。一方面,概率接近0的元素对应梯度极小,在反向传播中对梯度贡献可忽略不计,多个此类元素累积使得梯度消失,模型参数更新缓慢甚至停滞。另一方面,概率接近1的元素对应梯度可能极大,在反向传播中累积导致梯度爆炸,使模型参数更新幅度过大,无法收敛。
2. 除以结果大于 d k \sqrt{d_k} dk
若除以大于 d k \sqrt{d_k} dk的值,如 α d k \alpha\sqrt{d_k} αdk( α > 1 \alpha > 1 α>1),会过度缩放点积结果。这使得Softmax函数输入数值范围变小,输出概率分布相对均匀,各元素概率差异不明显。
在这种情况下,模型难以区分不同元素重要性,无法有效捕捉序列中关键信息,导致模型性能下降。因为自注意力机制依赖概率分布差异来聚焦重要信息,过于均匀分布削弱了这种聚焦能力。
3. 除以结果小于 d k \sqrt{d_k} dk
若除以小于 d k \sqrt{d_k} dk的值,如 β d k \beta\sqrt{d_k} βdk( 0 < β < 1 0 < \beta < 1 0<β<1),点积结果缩放不足,方差仍较大。Softmax函数输入数值方差大,输出概率分布仍会过度集中,类似不除以 d k \sqrt{d_k} dk的情况,导致梯度消失或爆炸问题,阻碍模型正常训练。
五、结论
在Transformer自注意力机制中,除以 d k \sqrt{d_k} dk是经过精心设计的关键操作。它源于对随机向量点积方差的理论分析,旨在稳定方差、平衡维度影响。不恰当的缩放,无论是不除以 d k \sqrt{d_k} dk,还是除以结果偏离 d k \sqrt{d_k} dk,都会因Softmax函数特性引发梯度问题或信息捕捉能力下降,严重影响模型性能。理解这一操作的原理和影响,对于深入理解Transformer架构及优化相关模型具有重要意义。
相关文章:

基于考研概率论知识解读 Transformer:为何自注意力机制要除以根号 dk
Transformer自注意力机制中除以 d k \sqrt{d_k} dk 深度剖析 【 Transformer 系列,故事从 d k \sqrt{d_k} dk 说起】 LLM这么火,Transformer厥功甚伟,某天心血来潮~,再去看看! 它长这个样子: 深入…...

网络安全学习81天(记录)
前言: 小迪安全,81天,开始了php代码审计 思路: 内容: #知识点: 1、审计漏洞-SQL 数据库注入挖掘 1、审计思路-正则搜索&功能追踪&辅助工具 3、审计类型-常规架构&MVC 架构&三方框架 #章…...
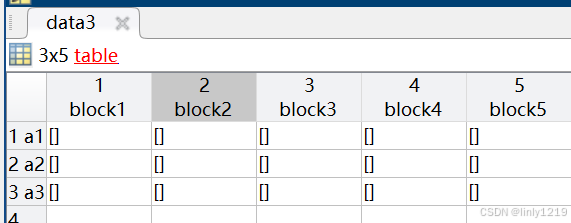
MATLAB学习笔记-table
1.在table中叠加table table 的每一列具有固定的数据类型。如果要让表的所有单元格都可以任意填充,就得让每一列都是 cell 类型,这样表中每个单元格都是“一个元胞”。创建时可以先构造一个 空 cell 数组(大小为行数列数)&#x…...

mybatisPlus(条件构造器API)
文章目录 目录一、mybatisPlus的介绍二、mybatisPlus的基础使用配置BaseMapper的基本CURD(增删改查) 三、wrapper(条件构造器)条件构造器(wrapper)通用API基础条件判断:进阶条件判断(…...

5G+工业互联网迈入规模化发展新阶段
百度安全验证 https://blog.csdn.net/qq_25467441/article/details/145036191?sharetypeblogdetail&sharerId145036191&sharereferPC&sharesourceqq_25467441&spm1011.2480.3001.8118 好看视频-轻松有收获 产业供给加速提升。国内主流模组厂商引领全球5G模组…...

【CI/CD构建】关于不小心将springMVC注解写在service层
背景 之前写一个接口的时候没有察觉到将RequestBody这个注解带到service层了。 今天提交代码的时候,插件没有检测到这个低级错误,导致试飞构建连maven编译都过不了,maven找不到程序包org.springframework.web.bind.annotation这个包 结果…...

《鸿蒙Next ArkTS:开启人工智能应用开发高效新旅程》
在当今科技飞速发展的时代,人工智能与鸿蒙Next的结合正成为开发者们关注的焦点。利用鸿蒙Next的ArkTS语言开发高效的人工智能驱动的应用程序,为我们带来了前所未有的机遇和创新空间。 了解ArkTS语言与鸿蒙Next ArkTS是一种基于TypeScript的静态类型脚本…...

Unity 3D游戏开发从入门进阶到高级
本文精心整理了Unity3D游戏开发相关的学习资料,涵盖入门、进阶、性能优化、面试和书籍等多个维度,旨在为Unity开发者提供全方位、高含金量的学习指南.欢迎收藏。 学习社区 Unity3D开发者 这是一个专注于Unity引擎的开发者社区,汇聚了众多Un…...

什么是SSH登录?SSH客户端软件有哪些?
一、SSH解释 SSH(Secure Shell)登录是一种用于计算机之间加密登录的网络协议。SSH登录允许用户通过互联网访问、控制和修改远程服务器。它提供了加密的通信通道,以保护敏感数据的机密性和完整性。SSH协议支持多种应用,包括SSH&…...

Ubuntu服务器提示:检测到存在恶意文件,补救思路
1. 确定文件类型 可以使用file命令来检查该文件的类型,这有助于判断它是否真的是一个恶意文件 file /path/to/the/file 2. 检查文件内容 使用strings命令查看文件内容,看是否有可疑的命令或脚本: strings /path/to/the/file 3. 扫描系统…...

【学习计算机视觉算法的基础及基本编码-基于Python语言--实例教程】
Python视觉算法实际从0-1实例编码 一、学习基础二、学习计算机视觉基础知识三、深度学习在计算机视觉中的应用四、实例项目五、实践与拓展 一、学习基础 数学基础 线性代数: 学习矩阵、向量的基本概念,包括矩阵的加法、乘法、转置等运算。理解矩阵的秩、…...

从零搭建一个Vue3 + Typescript的脚手架——day1
1.开发环境搭建 (1).配置vite vite简介 Vite 是一个由尤雨溪开发的现代化前端构建工具,它利用了浏览器对 ES 模块的原生支持,极大地提升了开发服务器的启动速度和热更新效率。Vite 不仅适用于 Vue.js,还支持 React、Svelte 等多种框架&…...

Pgsql存储占用分析
基础命令 -- 查询表大小 SELECT pg_total_relation_size(table_name);-- 查询表大小(不带索引) SELECT pg_table_size(table_name);-- 查询表索引大小 SELECT pg_indexes_size(table_name);-- 查询表具体大小 SELECT pg_relation_size(table_name); SEL…...

51c自动驾驶~合集46
我自己的原文哦~ https://blog.51cto.com/whaosoft/13050104 #世界模型会是L3自动驾驶的唯一解吗 三维空间占有率(3D Occupancy)预测的目的是预测三维空间中的每个体素是否被占有,如果被占有,则对应的体素将被标记。3D Semant…...

Elasticsearch:使用全文搜索在 ES|QL 中进行过滤 - 8.17
8.17 在 ES|QL 中引入了 match 和 qstr 函数,可用于执行全文过滤。本文介绍了它们的作用、使用方法、与现有文本过滤方法的区别、当前的限制以及未来的改进。 ES|QL 现在包含全文函数,可用于使用文本查询过滤数据。我们将回顾可用的文本过滤方法…...

《自动驾驶与机器人中的SLAM技术》ch8:基于 IESKF 的紧耦合 LIO 系统
目录 基于 IESKF 的紧耦合 LIO 系统 1 IESKF 的状态变量和运动过程 1.1 对名义状态变量的预测 1.2 对误差状态变量的预测及对协方差矩阵的递推 2 观测方程中的迭代过程 3 高维观测中的等效处理 4 NDT 和 卡尔曼滤波的联系 5 紧耦合 LIO 系统的主要流程 5.1 IMU 静止初始化 …...

引领图像编辑领域的新潮流!Edicho:实现跨图像一致编辑的新方法(港科蚂蚁)
在图像处理领域,如何实现跨图像的一致编辑一直是技术挑战。传统方法往往局限于单张图像的编辑,难以保证多张图像间编辑效果的一致性。香港科技大学、蚂蚁集团、斯坦福大学和香港中文大学联合提出Edicho,这一难题迎来了全新的解决方案。 总结如…...

459. 重复的子字符串【力扣】——kmp拼接字符串解法
常规kmp解答 class Solution { public:void getNext(int *next,string s){int j0;next[0]0;for(int i1;i<s.size();i){while(j>0 && s[i]!s[j]){jnext[j-1];}if(s[i]s[j]) j;next[i]j;}}bool repeatedSubstringPattern(string s) {if(s.size()0) return false;i…...

fpga 的时钟管理模块pll 跟 dcm
FPGA(Field-Programmable Gate Array,现场可编程门阵列)中的时钟管理模块(Clock Management Module, CMM)是用于生成和管理内部时钟信号的关键组件。两个常见的CMM类型是PLL(Phase-Locked Loop,…...

USB 驱动开发 --- Gadget 驱动框架梳理(一)
本文由 Linux 内核文档翻译与总结而来,个人学习笔记仅供参考。 Gadget 框架 在 USB 协议交互过程中,角色定义: the device driver is the master (or “client driver”) Linux 内核中称为 HCD(Host Controller Driver),负责与 …...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
