代码随想录Day34 | 62.不同路径,63.不同路径II,343.整数拆分,96.不同的二叉搜索树
代码随想录Day34 | 62.不同路径,63.不同路径II,343.整数拆分,96.不同的二叉搜索树
62.不同路径
动态规划第二集:
比较标准简单的一道动态规划,状态转移方程容易想到
难点在于空间复杂度的优化,详见代码
class Solution {public int uniquePaths(int m, int n) {// 标准的动态规划int[][] dp = new int[m + 1][n + 1];// 初始化时多加了一行一列,方便初始化dp[1][0] = 1;for (int i = 1; i < dp.length; i++) {for (int j = 1; j < dp[0].length; j++) {// 状态转移方程dp[i][j] = dp[i][j - 1] + dp[i - 1][j];}}return dp[m][n];}
}class Solution {public int uniquePaths(int m, int n) {// 标准的动态规划,空间优化版int[] dp = new int[n + 1];dp[1] = 1;for (int i = 1; i <= m; i++) {for (int j = 2; j <= n; j++) {// 状态转移方程// 只需要第 i 行与第 i-1 行的数据// dp[j - 1]已更新,是第 i 行的数据// dp[j]未更新,是第 i-1 行的数据dp[j] = dp[j - 1] + dp[j];}}return dp[n];}
}
63.不同路径II
相比上题只多了一个障碍的判断
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;// 空间优化思路同62题int[] dp = new int[n + 1];dp[1] = 1;for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {// 处理障碍情况if (obstacleGrid[i - 1][j - 1] == 1)dp[j] = 0;// 状态转移方程else dp[j] = dp[j - 1] + dp[j];}}return dp[n];}
}
343.整数拆分
动态规划问题,相对简单,想清楚状态转移方程就好,详见代码注释
class Solution {public int integerBreak(int n) {// dp[i] 的定义是 对 i 进行划分后的最大乘积int[] dp = new int[n + 1];dp[2] = 1;// 动态规划for (int i = 3; i <= n; i++) {// 循环进行划分for (int j = 1; j <= i / 2; j++) {// 状态转移方程// j * dp[i - j] 相当于是 在 i-j 中进行了多次划分// j * (i - j) 是只划分一次dp[i] = Math.max(dp[i], Math.max(j * dp[i - j], j * (i - j)));}}return dp[n];}
}
96.不同的二叉搜索树
动态规划:
要注意到,二叉树种类数目 = 左子树种类数目 * 右子树种类数目
class Solution {public int numTrees(int n) {// dp[i]定义为 i个节点时,互不相同的BST的种类数int[] dp = new int[n + 1];// 初始化:0个节点时只有一种dp[0] = 1;for (int i = 1; i <= n ; i++) {// 循环选择根节点为 jfor (int j = 1; j <= i; j++) {// dp[j - 1]为左子树种类数,dp[i - j]为右子树种类数// 左右数目相乘即为根节点为 j 时的种类数// 累加到 dp[i] 上dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];}
}
相关文章:

代码随想录Day34 | 62.不同路径,63.不同路径II,343.整数拆分,96.不同的二叉搜索树
代码随想录Day34 | 62.不同路径,63.不同路径II,343.整数拆分,96.不同的二叉搜索树 62.不同路径 动态规划第二集: 比较标准简单的一道动态规划,状态转移方程容易想到 难点在于空间复杂度的优化,详见代码 class Solution {public int uniq…...

vue.js辅助函数-mapMutations
在Vue.js中,使用辅助函数可以更方便地使用Vuex的mutation。而mapMutations就是Vuex提供的一个辅助函数,它可以将mutation映射到组件的methods中,使得我们可以在组件中直接调用mutation,而不需要手动进行commit。 mapMutations函数…...

Vue3组件设计模式:高可复用性组件开发实战
Vue3组件设计模式:高可复用性组件开发实战 一、前言 在Vue3中,组件设计和开发是非常重要的,它直接影响到应用的可维护性和可复用性。本文将介绍如何利用Vue3组件设计模式来开发高可复用性的组件,让你的组件更加灵活和易于维护。 二、单一职责…...

PHP 8.4 安装和升级指南
文章精选推荐 1 JetBrains Ai assistant 编程工具让你的工作效率翻倍 2 Extra Icons:JetBrains IDE的图标增强神器 3 IDEA插件推荐-SequenceDiagram,自动生成时序图 4 BashSupport Pro 这个ides插件主要是用来干嘛的 ? 5 IDEA必装的插件&…...

什么是 OpenResty
1、OpenResty简介 1.1 了解OpenResty OpenResty是一个基于 Nginx 与 Lua 的高性能 Web 平台,其内部集成了大量精良的 Lua 库、第三方模块以及大多数的依赖项。用于方便地搭建能够处理超高并发、扩展性极高的动态 Web 应用、Web 服务和动态网关。 简单地说OpenRes…...
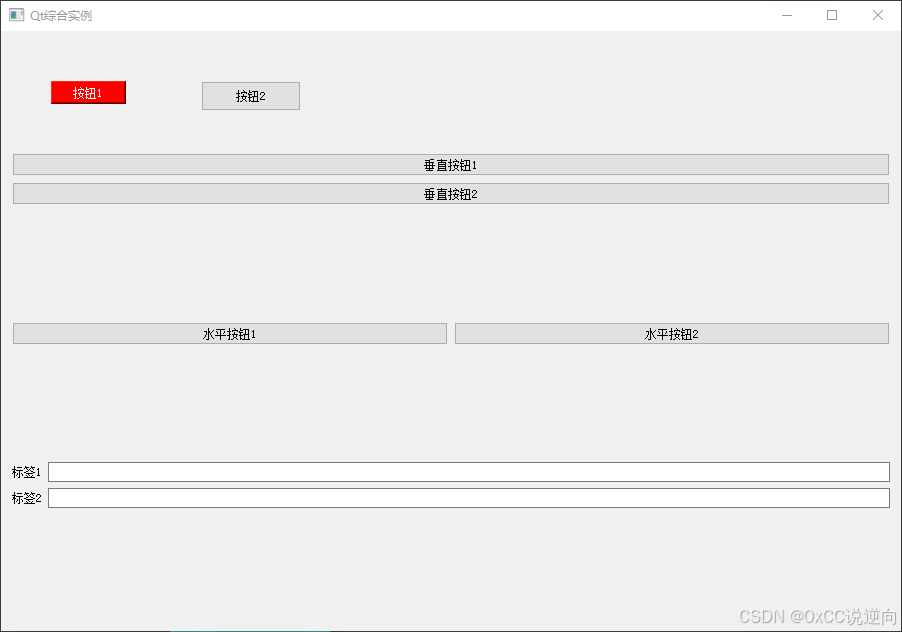
Windows图形界面(GUI)-QT-C/C++ - QT控件创建管理初始化
公开视频 -> 链接点击跳转公开课程博客首页 -> 链接点击跳转博客主页 目录 控件创建 包含对应控件类型头文件 实例化控件类对象 控件设置 设置父控件 设置窗口标题 设置控件大小 设置控件坐标 设置文本颜色和背景颜色 控件排版 垂直布局 QVBoxLayout …...

【计算机网络】lab8 DNS协议
🌈 个人主页:十二月的猫-CSDN博客 🔥 系列专栏: 🏀计算机网络_十二月的猫的博客-CSDN博客 💪🏻 十二月的寒冬阻挡不了春天的脚步,十二点的黑夜遮蔽不住黎明的曙光 目录 1. 前言 2.…...

了解linux中的“of_property_read_u32()”
of_property_read_u32(node, "post-pwm-on-delay-ms",&data->post_pwm_on_delay); /*根据"post-pwm-on-delay-ms",从属性中查找并读取一个32位整数*/ /*读到一个32位整数,保存到data->post_pwm_on_delay中*/ of_property_read_u32…...

iOS - Objective-C 底层中的内存屏障
1. 基本实现 // objc-os.h 中的内存屏障实现 #define OSMemoryBarrier() __sync_synchronize()// ARM 架构特殊处理 static ALWAYS_INLINE void OSMemoryBarrierBeforeUnlock() { #if defined(__arm__) || defined(__arm64__)OSMemoryBarrier(); #endif } 2. 解锁前的内存屏…...

阿里云服务器扩容系统盘后宝塔面板不显示扩容后的大小
解决方法步骤: 1. yum install cloud-utils-growpart xfsprogs -y 2.growpart /dev/vda 3 扩容系统盘的第3个分区 主要是这个命令1 3. fdisk -l 4. df -h 5. xfs_growfs /dev/vda3 主要是这个命令2 主要使用 df -Th 这个命令查看对应的文件系统类型 (1)、ext…...

c语言——【linux】多进程编程 【进程的创建,相关shell指令,进程状态切换,回收资源,守护进程等】
1.思维导图 2.进程的创建 函数原型:pid_t fork(void); 功能描述:以当前进程为父进程,创建一个子进程 进程链和进程扇的创建 3.多进程具体使用 3.1进程替换 exec 函数一族 int execl(const char *path, const char *arg, ... /* (char *) N…...

macos 搭建 ragflow 开发环境
ragflow 是一个很方便的本地 RAG 库。本文主要记录一下在本机的部署过程 1、总体架构说明 开发环境:macbook pro(m1),16G内存 512G固态 因本机的内存和硬盘比较可怜,所以在服务器上部署基础 docker 包,…...

信创改造-龙蜥操作系统搭载MySql、Tomcat等服务
龙蜥操作系统 Anolis OS 8 是 OpenAnolis 社区推出的完全开源、中立、开放的发行版,它支持多计算架构,也面向云端场景优化,兼容 CentOS 软件生态。Anolis OS 8 旨在为广大开发者和运维人员提供稳定、高性能、安全、可靠、开源的操作系统服务。…...

Java 数据结构 队列之双端队列 常用方法 示例代码 及其实现
目录 常用方法 示例代码 常见实现 Java中的双端队列(Deque,Double Ended Queue)是一种队列,它允许在队列的两端插入和删除元素。与普通队列(FIFO)不同,双端队列的元素可以从队列的两端进行添…...

【原创】大数据治理入门(2)《提升数据质量:质量评估与改进策略》入门必看 高赞实用
提升数据质量:质量评估与改进策略 引言:数据质量的概念 在大数据时代,数据的质量直接影响到数据分析的准确性和可靠性。数据质量是指数据在多大程度上能够满足其预定用途,确保数据的准确性、完整性、一致性和及时性是数据质量的…...

arcgis中生成格网矢量带高度
效果 1、数据准备 (1)矢量边界(miain.shp) (2)DEM(用于提取格网标高) (3)DSM(用于提取格网最高点) 2、根据矢量范围生成格网 模板范围选择矢量边界,像元宽度和高度根据坐标系来输入,我这边是4326的,所以输入的是弧度,输出格网矢量gewang.shp 3、分区统计 …...

使用gtsam添加OrientedPlane3Factor平面约束因子
在基于地面约束的SLAM优化中,已知的地面信息(如 plan.pcd 文件中的地面模型)可以用作一个先验约束,以帮助优化位姿估计。具体而言,这个过程涉及将地面模型和每个帧的位姿结合,以创建一个因子模型࿰…...

换了城市ip属地会变吗?为什么换了城市IP属地不变
当我们跨越城市的界限,从一个地方迁移到另一个地方时,许多日常使用的网络服务和应用程序都会感知到这种变化,其中一个显著的现象就是IP属地的变化。IP属地,即IP地址所在的地理位置信息,它通常与互联网服务提供商&#…...

移远通信多模卫星通信模组BG95-S5获得Skylo网络认证,进一步拓展全球卫星物联网市场
近日,全球领先的物联网整体解决方案供应商移远通信正式宣布,其支持“卫星蜂窝”多模式的高集成度NTN卫星通信模组BG95-S5已成功获得NTN网络运营商Skylo的网络认证。BG95-S5也成为了获得该认证的最新款移远卫星通信模组。 BG95-S5模组顺利获得Skylo认证&a…...

IntelliJ IDEA Type Hierarchy Scope Pattern 学习指南
IntelliJ IDEA Type Hierarchy Scope Pattern 学习指南 什么是 Type Hierarchy? Type Hierarchy 是 IntelliJ IDEA 提供的一个工具,允许开发者查看某个类的继承关系及其实现的接口结构。它是理解类关系的重要工具,尤其在处理复杂的继承体系…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
