【漏洞预警】FortiOS 和 FortiProxy 身份认证绕过漏洞(CVE-2024-55591)

---

一、产品简介

FortiOS是Fortinet公司核心的网络安全操作系统，广泛应用于FortiGate下一代防火墙，为用户提供防火墙、VPN、入侵防御、应用控制等多种安全功能。

FortiProxy则是Fortinet提供的企业级安全代理产品，主要用于内容过滤、Web访问控制和数据安全防护等场景。

下一代防火墙产品FortiGate（FortiOS）和代理产品FortiProxy中存在一个高危的认证绕过漏洞，漏洞编号为：CVE-2024-55591

二、漏洞描述

漏洞成因

漏洞主要与 FortiOS 和 FortiProxy 在处理认证逻辑时缺乏严格校验有关，导致远程攻击者可以在未授权的情况下绕过身份验证流程，获取超级管理员权限。

攻击者可通过向开放在互联网上的 FortiGate 管理接口（HTTPS 或 CLI Web Console）发送特定探测或恶意请求来触发该漏洞，从而在设备上执行多种非法操作。

漏洞影响

攻击者成功利用该漏洞可在 FortiGate/FortiProxy 设备上执行任意管理操作，包括创建或重置管理员账户、读取或修改防火墙策略、配置 SSL VPN 并进一步进行网络横向移动等。在此同时攻击者可在未授权情况下获得管理权限，并对防火墙配置进行修改，进而威胁内部网络安全。

三、影响版本

受影响的产品和版本包括：

• 7.0.0 <= FortiOS 7.0.* <= 7.0.16
• 7.0.0 <= FortiProxy 7.0.* <= 7.0.19
• 7.2.0 <= FortiProxy 7.2.* <= 7.2.12

升级后的安全版本：

• FortiOS 7.0.* >= 7.0.17
• FortiProxy 7.0.* >= 7.0.20
• FortiProxy 7.2.* >= 7.2.13

四、漏洞检测方法

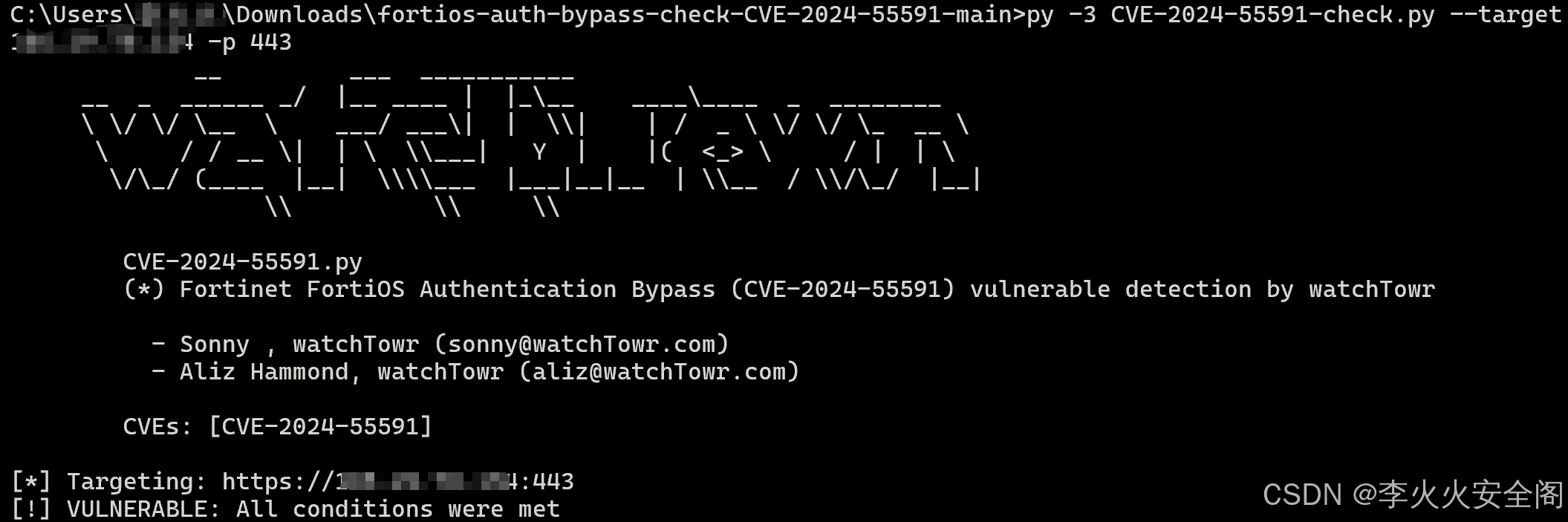
POC：https://github.com/watchtowrlabs/fortios-auth-bypass-check-CVE-2024-55591

使用方法：py -3 CVE-2024-55591-check.py --target 127.0.0.1 -p 443

五、解决方案

临时缓解方式以下几点：

1、立即关闭防火墙管理接口对公网的访问

将FortiGate/FortiProxy的管理端口（HTTPS/SSH/CLI 等）限制在受信任的内部网络或专用管理网络，避免直接暴露在互联网上。使用防火墙或安全策略过滤管理端口仅允许特定 IP 地址访问。

2. 监控可疑账号和配置变更

检查系统日志（logdesc=“Admin login successful” 等）中是否存在来源于可疑 IP（如 127.0.0.1、8.8.8.8 等）且使用 jsconsole UI 的异常登录记录。监控是否存在异常的管理员账号（如随机字母数字组合）或 SSL VPN 配置变更。

3. 排查可疑文件或后门

若怀疑设备已被攻陷，可导出配置并对关键配置及文件系统进行完整性校验；如有异常，建议联系 Fortinet 支持或专业安全团队协助调查。

4. 变更所有管理员账户及 VPN 用户密码

如果怀疑攻击者已获取管理凭据，应立即重置所有本地管理员密码、撤销旧证书、更新 API 密钥等。

修复方案如下：

1、官方补丁升级

Fortinet 在 2025 年 1 月 14 日发布了安全更新补丁，修复了该认证绕过漏洞（CVE-2024-55591），请尽快升级至安全的 FortiOS/FortiProxy 版本。

补丁下载：https://docs.fortinet.com/upgrade-tool

2、禁用 HTTP/HTTPS 管理界面；

3、通过本地策略限制可以到达管理接口的 IP 地址。