当前位置： 首页 > news >正文

基于 K-Means 聚类分析实现人脸照片的快速分类

news 2026/1/18 22:07:29

注：本文在创作过程中得到了 ChatGPT、DeepSeek、Kimi 的智能辅助支持，由作者本人完成最终审阅。

在 “视频是不能 P 的” 系列文章中，博主曾先后分享过人脸检测、人脸识别等相关主题的内容。今天，博主想和大家讨论的是人脸分类问题。你是否曾在人群中认错人，或是盯着熟人的照片却一时想不出对方的名字？这种 “脸盲症” 的困扰，不仅在生活中令人感到尴尬，在整理照片时更是让人头疼不已。想象一下，某次聚会结束后，你的手机里存了上百张照片——有你的笑脸、朋友的自拍，甚至还有一部分陌生面孔混杂其中。手动将这些照片按人物分类，不仅费时费力，还可能会因为 “脸盲” 而频繁出错。此时，你是否期待有一种技术，可以像魔法一样，自动将这些照片按人物分类？事实上，这种 “魔法” 已经存在，它的名字叫做 K-Means 聚类分析。作为一种经典的无监督学习算法，K-Means 能够通过分析人脸特征，自动将相似的面孔归类到一起，完全无需人工干预。接下来，为了彻底根治 “脸盲症”，我们将详细介绍如何使用 K-Means 聚类分析来实现这一目标，哈利·波特拥有魔法，而我们则拥有科技。

相关文章：

基于 K-Means 聚类分析实现人脸照片的快速分类

注：本文在创作过程中得到了 ChatGPT、DeepSeek、Kimi 的智能辅助支持，由作者本人完成最终审阅。 在 “视频是不能 P 的” 系列文章中，博主曾先后分享过人脸检测、人脸识别等相关主题的内容。今天，博主想和大家讨论的是人脸分类问题。你是否曾在人群中认错人，或是盯着熟人的…...

编程日记 2025/1/19 10:28:31

【漏洞预警】FortiOS 和 FortiProxy 身份认证绕过漏洞(CVE-2024-55591)

文章目录 一、产品简介二、漏洞描述三、影响版本四、漏洞检测方法五、解决方案 一、产品简介 FortiOS是Fortinet公司核心的网络安全操作系统，广泛应用于FortiGate下一代防火墙，为用户提供防火墙、VPN、入侵防御、应用控制等多种安全功能。 FortiProxy则…...

编程日记 2025/1/19 10:23:25

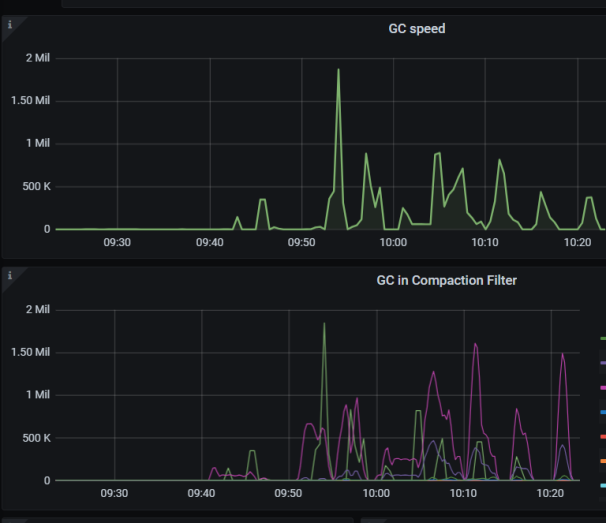
7.5.4 MVCC优化测试

作者： h5n1 原文来源： https://tidb.net/blog/4e02d900 1. 背景 由于MVCC 版本数量过多导致rocksdb扫描key数量过多影响SQL执行时间是tidb经常出现问的问题，tidb也一直在致力于优化该问题。 一些优化方式包括比： (1) 从传统…...

编程日记 2025/1/19 10:22:23

STM32 FreeRTOS 事件标志组

目录 事件标志组简介 基本概念 1、事件位（事件标志） 2、事件组 事件组和事件位数据类型 事件标志组和信号量的区别 事件标志组相关API函数介绍 事件标志组简介 基本概念 当在嵌入式系统中运行多个任务时，这些任务可能需要相互通信&am…...

编程日记 2025/1/19 10:21:22

生成树机制实验

1 实验内容 1、基于已有代码，实现生成树运行机制，对于给定拓扑(four_node_ring.py)，计算输出相应状态下的生成树拓扑 2、构造一个不少于7个节点，冗余链路不少于2条的拓扑，节点和端口的命名规则可参考four_node_ring.py，使用stp程序计算输出生成树拓扑 2 实验原理 一、…...

编程日记 2025/1/19 10:18:19

企业分类相似度筛选实战：基于规则与向量方法的对比分析

文章目录 企业表相似类别筛选实战项目背景介绍效果展示基于规则的效果基于向量相似的效果 说明相关文章推荐 企业表相似类别筛选实战 项目背景 在当下RAG（检索增强生成）技术应用不断发展的背景下，掌握文本相似算法不仅能够助力信息检索&…...

编程日记 2025/1/19 10:16:17

2024年博客之星年度评选—创作影响力评审入围名单公布

2024年博客之星活动地址https://www.csdn.net/blogstar2024 TOP 300 榜单排名 用户昵称博客主页 身份 认证 评分 原创 博文 评分 平均 质量分评分 互动数据评分 总分排名三掌柜666三掌柜666-CSDN博客1001002001005001wkd_007wkd_007-CSDN博客1001002001005002栗筝ihttps:/…...

编程日记 2025/1/19 10:15:12

递归40题！再见递归

简介：40个问题，有难有易，均使用递归完成，需要C/C的指针、字符串、数组、链表等基础知识作为基础。 1、数字出现的次数 由键盘录入一个正整数，求该整数中每个数字出现的次数。 输入：19931003 输出&#xf…...

编程日记 2025/1/19 10:11:07

社区版Dify实现文生视频 LLM+ComfyUI+混元视频

社区版Dify实现文生视频 LLMComfyUI混元视频 一、 社区版Dify实现私有化混元视频效果二、为什么社区版Dify可以在对话框实现文生视频？LLMComfyUI混元视频 实现流程图（重点）1. 文生视频模型支持ComfyUI2. ComfyUI可以轻松导出API实现封装3. Di…...

编程日记 2025/1/19 10:09:05

【LLM】Openai-o1及o1类复现方法

note 可以从更为本质的方案出发，通过分析强化学习的方法，看看如何实现o1，但其中的核心就是在于，如何有效地初始化策略、设计奖励函数、实现高效的搜索算法以及利用强化学习进行学习和优化。 文章目录 note一、Imitate, Explore, …...

编程日记 2025/1/19 10:08:04

jlatexmath-android如何实现自定义渲染字符

使用jlatexmath-android的过程，如果出现个别字符渲染不了，会导致无法显示 常用的做法是新增自定义字体切换系统默认字体渲染，下面我们介绍第2种方法。 修改流程： 1、到jlatexmath-android的官网下载源码到本地，导入…...

编程日记 2025/1/19 10:03:57

dockerhub上一些镜像

K8s下网络排障工具 https://hub.docker.com/r/nicolaka/netshoot ex kubectl run tmp-shell --rm -i --tty --image nicolaka/netshoot -- /bin/bash # 主机的net ns下运行 kubectl run tmp-shell --rm -i --tty --overrides{"spec": {"hostNetwork": tru…...

编程日记 2025/1/19 10:02:52

Python 爬虫学习指南与资料分享

Python爬虫学习资料 Python爬虫学习资料 Python爬虫学习资料 在数字化浪潮中，Python 爬虫作为强大的数据获取工具，为众多领域提供关键支持。想要系统掌握这门技术，以下的学习指南与资料分享将为你照亮前行道路。 一、学习指南 入门奠基 …...

编程日记 2025/1/19 9:55:46

TypeScript特有运算符和操作符

文章目录 TypeScript 特有运算符1. keyof2. typeof3. in4. extends5. is6. as 和 <Type>7. never8. readonly9. ?10. []11. | 和 &12. !13. ?? 和 ?. 总结 TypeScript 特有运算符 1. keyof 作用&#xff1a;用于获取对象类型的所有键&#xff08;属性名&#x…...

编程日记 2025/1/19 9:54:45

介绍下常用的前端框架及时优缺点

以下是一些常用的前端框架及其优缺点介绍&#xff1a; React • 优点 • 组件化架构&#xff1a;可构建可复用的UI组件&#xff0c;提高开发效率和组件可维护性。 • 虚拟DOM&#xff1a;高效更新页面&#xff0c;减少直接操作DOM的性能开销。 • 灵活性和可扩展性&#xf…...

编程日记 2025/1/19 9:44:32

MATLAB算法实战应用案例精讲-【数模应用】图形变换和复杂图形组合（附python和MATLAB代码实现）

目录 前言 算法原理 变换 1二维变换 1.1缩放 1.2 翻转 1.3剪切 1.4 旋转 2齐次坐标 2.1引入齐次坐标的原因 2.2 二维齐次坐标 2.3二维仿射变换 2.4逆变换 4组合变换 5三维变换（由二维变换推理而来） 5.1三维齐次坐标 5.2 三维仿射变换 5.3 缩放和平移 5.4…...

编程日记 2025/1/19 9:41:29

SpringMVC 实战指南：打造高效 Web 应用的秘籍

第一章&#xff1a;三层架构和MVC 三层架构&#xff1a; 开发服务器端&#xff0c;一般基于两种形式&#xff0c;一种 C/S 架构程序&#xff0c;一种 B/S 架构程序使用 Java 语言基本上都是开发 B/S 架构的程序&#xff0c;B/S 架构又分成了三层架构三层架构&#xff1a; 表现…...

编程日记 2025/1/19 9:38:26

doris: Flink导入数据

使用 Flink Doris Connector 可以实时的将 Flink 产生的数据&#xff08;如&#xff1a;Flink 读取 Kafka&#xff0c;MySQL 中的数据&#xff09;导入到 Doris 中。 使用限制​ 需要依赖用户部署的 Flink 集群。 使用 Flink 导入数据​ 使用 Flink 导入数据&#xff0c;详…...

编程日记 2025/1/19 9:36:24

Nginx在Linux中的最小化安装方式

1. 安装依赖 需要安装的东西&#xff1a; wget​&#xff0c;方便我们下载Nginx的包。如果是在Windows下载&#xff0c;然后使用SFTP上传到服务器中&#xff0c;那么可以不安装这个软件包。gcc g​&#xff0c;Nginx是使用C/C开发的服务器&#xff0c;等一下安装会用到其中的…...

编程日记 2025/1/19 9:31:19

CSS布局新视角：BFC（块级格式化上下文）的作用与优势

在CSS布局的世界中&#xff0c;BFC&#xff08;Block Formatting Context&#xff0c;块级格式化上下文&#xff09;是一个既重要又神秘的概念。它不仅是解决复杂布局问题的关键工具&#xff0c;也是提升页面性能和用户体验的重要手段。本文将从新视角出发&#xff0c;深入探讨…...

编程日记 2025/1/19 9:26:14

vscode里如何用git

打开vs终端执行如下&#xff1a; 1 初始化 Git 仓库&#xff08;如果尚未初始化&#xff09; git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

编程新知 2025/8/24 20:45:38

XCTF-web-easyupload

试了试php&#xff0c;php7&#xff0c;pht&#xff0c;phtml等&#xff0c;都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接&#xff0c;得到flag...

编程新知 2026/1/16 3:56:34

Debian系统简介

目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版&#xff…...

编程新知 2026/1/16 14:12:57

微服务商城-商品微服务

数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

编程新知 2026/1/15 4:57:55

Linux 内存管理实战精讲：核心原理与面试常考点全解析

Linux 内存管理实战精讲&#xff1a;核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用&#xff0c;还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

编程新知 2026/1/15 5:05:14

Netty从入门到进阶（二）

二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架&#xff0c;用于…...

编程新知 2026/1/15 6:33:51

uniapp 字符包含的相关方法

在uniapp中&#xff0c;如果你想检查一个字符串是否包含另一个子字符串&#xff0c;你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的&#xff0c;但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

编程新知 2025/9/28 19:00:18

在树莓派上添加音频输入设备的几种方法

在树莓派上添加音频输入设备可以通过以下步骤完成&#xff0c;具体方法取决于设备类型&#xff08;如USB麦克风、3.5mm接口麦克风或HDMI音频输入&#xff09;。以下是详细指南&#xff1a; 1. 连接音频输入设备 USB麦克风/声卡&#xff1a;直接插入树莓派的USB接口。3.5mm麦克…...

编程新知 2025/11/22 14:54:34

机器学习的数学基础：线性模型

线性模型 线性模型的基本形式为&#xff1a; f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法&#xff0c;得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

编程新知 2025/10/2 9:07:50

2025年- H71-Lc179--39.组合总和(回溯,组合）--Java版

1.题目描述 2.思路 当前的元素可以重复使用。 &#xff08;1&#xff09;确定回溯算法函数的参数和返回值&#xff08;一般是void类型&#xff09; &#xff08;2&#xff09;因为是用递归实现的&#xff0c;所以我们要确定终止条件 &#xff08;3&#xff09;单层搜索逻辑 二…...

编程新知 2026/1/15 8:18:11