全同态加密理论、生态现状与未来展望(中2)
《全同态加密理论、生态现状与未来展望》系列由lynndell2010@gmail.com和mutourend2010@gmail.com整理原创发布,分为上中下三个系列:
- 全同态加密理论、生态现状与未来展望(上):专注于介绍全同态加密理论知识。
- 全同态加密理论、生态现状与未来展望(中1):专注于介绍全同态加密四代算法中第一代第二代FHE算法的衍化历程。
- 全同态加密理论、生态现状与未来展望(中2):专注于介绍全同态加密四代算法中第三代第四代FHE算法的衍化历程。
- 全同态加密理论、生态现状与未来展望(下):专注于介绍当前全同态加密生态现状及未来展望。
整个系列内容可能存在纰漏,希望能得到大家的反馈,有任何问题欢迎邮件联系lynndell2010@gmail.com和mutourend2010@gmail.com,或在本文下方评论留言。
3.3 第3代:基于LWE和RLWE

图 7: 第 3 代:基于 LWE 和 RLWE
3.3.1 GSW13
Homomorphic Encryption from Learning with Errors:Conceptually-Simpler, Asymptotically-Faster, Attribute-Based
安全参数为 λ \lambda λ,电路深度为 L L L。模为 q q q、噪声分布 χ \chi χ、维数 n n n 以及 m m m。 其中,分布 χ \chi χ是 Z \mathbb{Z} Z上的噪声高斯分布, m = 2 n log q m=2n\log q m=2nlogq。令 l = ⌈ log q ⌉ l = \lceil \log q \rceil l=⌈logq⌉, N = ( n + 1 ) l N = (n+1)l N=(n+1)l。
-
密钥生成: 选择随机向量 s ′ ← Z q n \mathbf{s}' \leftarrow \mathbb{Z}^n_q s′←Zqn,私钥为 s k = s = ( 1 , s ′ ) ∈ Z q n + 1 sk = \mathbf{s} = (1, \mathbf{s}') \in \mathbb{Z}^{n+1}_q sk=s=(1,s′)∈Zqn+1。
有以下等式成立:
Powerof2 ( s ) = ( s , 2 s , ⋯ , 2 l − 1 s ) m o d q = ( 1 , 2 , ⋯ , 2 l − 1 , s ′ , 2 s ′ , ⋯ , 2 l − 1 s ′ ) m o d q \text{Powerof2}(\mathbf{s}) = (\mathbf{s}, 2\mathbf{s}, \cdots, 2^{l-1}\mathbf{s}) \mod q= (1, 2, \cdots, 2^{l-1},\mathbf{s}', 2\mathbf{s}', \cdots, 2^{l-1}\mathbf{s}') \mod q Powerof2(s)=(s,2s,⋯,2l−1s)modq=(1,2,⋯,2l−1,s′,2s′,⋯,2l−1s′)modq选取随机矩阵 A ′ ← Z q m × n \mathbf{A}' \leftarrow \mathbb{Z}^{m \times n}_q A′←Zqm×n和噪声向量 e ← χ m \mathbf{e} \leftarrow \chi^m e←χm,计算
b : = A ′ ⋅ s ′ + e b := \mathbf{A}' \cdot \mathbf{s}' + \mathbf{e} b:=A′⋅s′+e
令 A \mathbf{A} A为 n + 1 n+1 n+1列矩阵,由向量 b \mathbf{b} b和矩阵 A ′ \mathbf{A}' A′构成
A = [ b ∣ − A ′ ] ∈ Z q m × ( n + 1 ) \mathbf{A} = [\mathbf{b} | -\mathbf{A}'] \in \mathbb{Z}_q^{m \times (n+1)} A=[b∣−A′]∈Zqm×(n+1)
公钥为 p k = A pk = \mathbf{A} pk=A。
注意,有以下等式成立 A ⋅ s = [ b ∣ − A ′ ] ⋅ ( 1 , s ′ ) = ( A ′ ⋅ s ′ + e ) − A ′ s ′ = e \mathbf{A} \cdot \mathbf{s} =[\mathbf{b} | -\mathbf{A}']\cdot (1,\mathbf{s}') =(\mathbf{A}' \cdot \mathbf{s}' + \mathbf{e})-\mathbf{A}'\mathbf{s}' = \mathbf{e} A⋅s=[b∣−A′]⋅(1,s′)=(A′⋅s′+e)−A′s′=e -
加密:
消息为 m ∈ { 0 , 1 } m \in \{0, 1\} m∈{0,1},选取随机矩阵 R ∈ { 0 , 1 } N × m \mathbf{R} \in \{0, 1\}^{N \times m} R∈{0,1}N×m,如下计算:
C : = m ⋅ I N + R ⋅ A \mathbf{C} :=m \cdot \mathbf{I}_N+\mathbf{R} \cdot \mathbf{A} C:=m⋅IN+R⋅A
其中, I N \mathbf{I}_N IN是 N × N N \times N N×N的单位矩阵。则密文为 C \mathbf{C} C。为满足同态性,密文长度不变,通常记为 Flatten ( C ) \text{Flatten}(\mathbf{C}) Flatten(C)。 -
解密: 输入私钥 s \mathbf{s} s和密文 C \mathbf{C} C,如下计算:
C s = ( m ⋅ I N + R ⋅ A ) s = m ⋅ I N s + R e = m ⋅ I N s + e ∗ = m ⋅ Powersof2 ( s ) + e ∗ \mathbf{C}\mathbf{s} =(m \cdot \mathbf{I}_N+\mathbf{R} \cdot \mathbf{A})\mathbf{s} =m \cdot \mathbf{I}_N\mathbf{s}+\mathbf{R}\mathbf{e} =m \cdot \mathbf{I}_N\mathbf{s}+\mathbf{e}^* =m\cdot\text{Powersof2}(\mathbf{s})+\mathbf{e}^* Cs=(m⋅IN+R⋅A)s=m⋅INs+Re=m⋅INs+e∗=m⋅Powersof2(s)+e∗
其中, m I N s = ( m , m s ′ ) m\mathbf{I}_N\mathbf{s}=(m,ms') mINs=(m,ms′)取出 m m m, R ⋅ e = e ∗ ≈ 0 \mathbf{R} \cdot \mathbf{e}=\mathbf{e}^*\approx 0 R⋅e=e∗≈0。 -
同态加法: C + C ′ = ( m + m ′ ) ⋅ I N + ( R + R ′ ) ⋅ A \mathbf{C}+\mathbf{C}' =(m+m')\cdot \mathbf{I}_N+(\mathbf{R}+\mathbf{R}') \cdot \mathbf{A} C+C′=(m+m′)⋅IN+(R+R′)⋅A
通常记为 Flatten ( C + C ′ ) \text{Flatten}(\mathbf{C}+\mathbf{C}') Flatten(C+C′)。 -
解密:
( C + C ′ ) s = ( ( m + m ′ ) ⋅ I N + ( R + R ′ ) ⋅ A ) s = ( m + m ′ ) ⋅ I N s + ( R + R ′ ) e (\mathbf{C}+\mathbf{C}')\mathbf{s}=((m+m') \cdot \mathbf{I}_N+(\mathbf{R}+\mathbf{R}') \cdot \mathbf{A})\mathbf{s}=(m+m') \cdot \mathbf{I}_N\mathbf{s}+(\mathbf{R}+\mathbf{R}')\mathbf{e} (C+C′)s=((m+m′)⋅IN+(R+R′)⋅A)s=(m+m′)⋅INs+(R+R′)e -
同态乘法: C ∙ C ′ = ( m ⋅ I N + R ⋅ A ) ∙ ( m ′ ⋅ I N + R ′ ⋅ A ) \mathbf{C}\bullet\mathbf{C}' =(m\cdot \mathbf{I}_N+\mathbf{R} \cdot\mathbf{A})\bullet(m'\cdot \mathbf{I}_N+\mathbf{R}' \cdot\mathbf{A}) C∙C′=(m⋅IN+R⋅A)∙(m′⋅IN+R′⋅A)
通常记为 Flatten ( C ∙ C ′ ) \text{Flatten}(\mathbf{C} \bullet\mathbf{C}') Flatten(C∙C′)。 -
解密:
由前面的解密步骤可知: C s = m ⋅ Powersof2 ( s ) + e ∗ \mathbf{C}\mathbf{s}=m\cdot\text{Powersof2}(\mathbf{s})+\mathbf{e}^* Cs=m⋅Powersof2(s)+e∗,所以如下解密:
( C ∙ C ′ ) s = C ∙ ( m ′ ⋅ Powersof2 ( s ) + e ′ ) = m ′ C Powersof2 ( s ) + C e ′ = m ′ ( m Powersof2 ( s ) + e ) + C e ′ = m ′ m Powersof2 ( s ) + m ′ e + C e ′ \begin{aligned} &(\mathbf{C}\bullet\mathbf{C}') \mathbf{s}\\ &=\mathbf{C}\bullet (m' \cdot \text{Powersof2}(\mathbf{s})+\mathbf{e'})\\ &=m'\mathbf{C}\text{Powersof2}(\mathbf{s})+\mathbf{C}\mathbf{e'}\\ &=m'(m\text{Powersof2}(\mathbf{s})+\mathbf{e})+\mathbf{C}\mathbf{e'}\\ &=m'm\text{Powersof2}(\mathbf{s})+m'\mathbf{e}+\mathbf{C}\mathbf{e'} \end{aligned} (C∙C′)s=C∙(m′⋅Powersof2(s)+e′)=m′CPowersof2(s)+Ce′=m′(mPowersof2(s)+e)+Ce′=m′mPowersof2(s)+m′e+Ce′
当 m ′ e + C e ′ ≤ ( N + 1 ) E = ( ( n + 1 ) l + 1 ) ⋅ 2 n B log q m'\mathbf{e}+\mathbf{C}\mathbf{e'}\le (N+1)E=((n+1)l+1)\cdot 2nB\log q m′e+Ce′≤(N+1)E=((n+1)l+1)⋅2nBlogq时,可解密成功。
经过深度为 L L L的电路计算后,结果密文的噪声至多为 ( N + 1 ) L E (N+1)^LE (N+1)LE。因此,需满足一下条件才能正确解密:
( N + 1 ) L E = ( ( n + 1 ) l + 1 ) L ⋅ 2 n B log q < q / 8 (N+1)^L E=((n+1)l+1)^L \cdot 2nB\log q <q/8 (N+1)LE=((n+1)l+1)L⋅2nBlogq<q/8
GSW 方案的主要缺点是较高的通信成本(密文相对于对应的明文较大)和计算复杂性。为了减少计算开销,提出了各种优化方法以改进启动过程(图7)。
3.3.2 TRLWE18
TFHE: Fast Fully Homomorphic Encryption over the Torus
令 R = Z [ x ] / ⟨ x d + 1 ⟩ R = \mathbb{Z}[x]/\langle x^d + 1 \rangle R=Z[x]/⟨xd+1⟩。其中, d d d是2的幂次方。令 T = R [ x ] / ⟨ x d + 1 ⟩ m o d 1 T = \mathbb{R}[x]/\langle x^d + 1 \rangle \mod 1 T=R[x]/⟨xd+1⟩mod1和 R 2 = F 2 [ x ] / ⟨ x d + 1 ⟩ R_2 = \mathbb{F}_2[x]/\langle x^d + 1 \rangle R2=F2[x]/⟨xd+1⟩,即 R 2 R_2 R2中的任何元素都是具有二进制系数的 R R R中的多项式。
TRLWE18方案构造如下:
-
密钥生成: 输入安全参数 λ \lambda λ,输出小的私钥 s ∈ R 2 n \mathbf{s}\in R_2^n s∈R2n。
-
加密: 输入私钥 s ∈ R 2 n \mathbf{s}\in R_2^n s∈R2n,错误参数 α \alpha α和消息 m ∈ T m \in T m∈T。然后,选择一个均匀随机的掩码 a ∈ T n a \in T^n a∈Tn,并选择一个小的噪声 e ∈ χ e \in \chi e∈χ。其中, χ \chi χ 是一个B有界分布,则密文为:
c : = ( a , b ) = ( a , s ⋅ a + m + e ) ∈ T n × T \mathbf{c} := (\mathbf{a}, b)=(\mathbf{a}, \mathbf{s} \cdot \mathbf{a} + m + e) \in T^n \times T c:=(a,b)=(a,s⋅a+m+e)∈Tn×T -
解密: 输入私钥 s ∈ R 2 n s \in R_2^n s∈R2n和密文 c ∈ T n + 1 \mathbf{c} \in T^{n+1} c∈Tn+1,计算密文 c \mathbf{c} c的秘密线性 κ \kappa κ-Lipschitz函数 φ s \varphi_s φs(称为相位)。该相位 φ s : T n × T → T \varphi_s:T^n \times T \to T φs:Tn×T→T 满足:
φ s ( a , b ) = b − s ⋅ a \varphi_s(\mathbf{a}, b) = b - s \cdot \mathbf{a} φs(a,b)=b−s⋅a
注意,该函数由私钥 s ∈ R 2 n \mathbf{s} \in R_2^n s∈R2n参数化。相位 φ s ( c ) \varphi_\mathbf{s}(\mathbf{c}) φs(c)接近实际的消息:
φ s ( c ) = s ⋅ a + m + e − s ⋅ a = m + e \varphi_\mathbf{s}(\mathbf{c}) = \mathbf{s} \cdot \mathbf{a} + m + e - \mathbf{s} \cdot \mathbf{a} = m + e φs(c)=s⋅a+m+e−s⋅a=m+e
最后,将 φ s ( c ) \varphi_s(c) φs(c) 四舍五入到消息空间 M ⊂ T M \subset T M⊂T 中的最近点。 -
(同态)密文的线性组合:
设 c 1 , … , c p \mathbf{c}_1, \dots, \mathbf{c}_p c1,…,cp为 p p p个独立的密文,具有相同的密钥 s \mathbf{s} s,并且设 f 1 , … , f p f_1, \dots, f_p f1,…,fp为 R R R中的整数多项式。如下构造线性组合的密文:
c = ∑ i = 1 p f i ⋅ c i \mathbf{c} = \sum_{i=1}^p f_i \cdot \mathbf{c}_i c=i=1∑pfi⋅ci
要求误差幅度保持小于 1 / 4 1/4 1/4, ∣ ∣ e ∣ ∣ ∞ ≤ 1 / 4 ||e||_{\infty} \leq 1/4 ∣∣e∣∣∞≤1/4。 -
解密:
Dec s ( c ) = ∑ i = 1 p f i ⋅ Dec s ( c i ) \text{Dec}_\mathbf{s}(\mathbf{c})=\sum_{i=1}^p f_i \cdot \text{Dec}_\mathbf{s}(\mathbf{c}_i) Decs(c)=i=1∑pfi⋅Decs(ci)
密文可以线性组合,从而得到一个新的密文,解密后可以获得明文的线性组合。
3.4 第4代:基于LWE和RLWE

图 8: 基于基于 LWE 和 RLWE 的第四代 FHE
3.4.1 CKKS16
Homomorphic Encryption for Arithmetic of Approximate Numbers
令 R = Z [ x ] / ⟨ x d + 1 ⟩ R = \mathbb{Z}[x]/\langle x^d + 1 \rangle R=Z[x]/⟨xd+1⟩ 且 d = 2 M d = 2^M d=2M。对于基数 p p p、模 q 0 q_0 q0和自然数 L L L(选择的层次),令 q ℓ = p ℓ ⋅ q 0 q_\ell = p^\ell \cdot q_0 qℓ=pℓ⋅q0对于 ℓ = 1 , … , L \ell = 1, \ldots, L ℓ=1,…,L。注意,层次 ℓ \ell ℓ的密文是 R q ℓ R_{q_\ell} Rqℓ中的一个向量。考虑以下相关分布:对于实数 σ \sigma σ, D G ( σ 2 ) DG(\sigma^2) DG(σ2)是一个在 Z d \mathbb{Z}^d Zd上的离散高斯分布,从独立的离散高斯分布中采样,每个分量的方差为 σ 2 \sigma^2 σ2。对于 0 ⟨ ρ ⟨ 1 0 \langle \rho \langle 1 0⟨ρ⟨1的实数,分布 Z O ( ρ ) ZO(\rho) ZO(ρ)是一个在 { − 1 , 0 , 1 } d \{-1, 0, 1\}^d {−1,0,1}d上的分布。其中, 0 0 0的概率为 1 − ρ 1 - \rho 1−ρ,而 − 1 -1 −1或 1 1 1的概率为 ρ 2 \frac{\rho}{2} 2ρ。最后, χ \chi χ是一个 B B B-有界分布。
层次型CKKS16方案构造如下:
-
密钥生成: 输入安全参数 λ \lambda λ,选择 M M M、整数 h h h和 t t t,以及实数 σ \sigma σ,使得对关联的RLWE实例,最佳攻击的复杂度为 2 λ 2^\lambda 2λ。私钥为 s k = ( 1 , s ) sk = (1, s) sk=(1,s)。其中, s ∈ χ s \in \chi s∈χ。生成一个均匀随机的 a ∈ R q L a \in R_{q_L} a∈RqL,并计算 b = − a s + e m o d q L b=-as + e \mod q_L b=−as+emodqL。其中, e e e 为 D G ( σ 2 ) DG(\sigma^2) DG(σ2)。最后,采样 a ′ ∈ R t ⋅ q L a'\in R_{t \cdot q_L} a′∈Rt⋅qL和 e ′ ∈ D G ( σ 2 ) e'\in DG(\sigma^2) e′∈DG(σ2),并计算 b ′ = − a s + e ′ + t s ′ m o d t ⋅ q L b' = -as + e' + ts' \mod t \cdot q_L b′=−as+e′+ts′modt⋅qL。公钥为 p k = ( b , a ) pk = (b, a) pk=(b,a)和评估密钥为 e v k = ( b ′ , a ′ ) evk = (b', a') evk=(b′,a′)。
-
加密: 消息为 m ∈ R m \in R m∈R,公钥为 p k = ( b , a ) ∈ R q L 2 pk=(b,a) \in R_{q_L}^2 pk=(b,a)∈RqL2,随机选择 v ∈ Z O ( 1 / 2 ) v \in ZO(1/2) v∈ZO(1/2)和噪声 e 0 , e 1 ∈ D G ( σ 2 ) e_0, e_1 \in DG(\sigma^2) e0,e1∈DG(σ2),如下计算密文
c = ( β , α ) = v ( b , a ) + ( m + e 0 , e 1 ) m o d q ℓ = ( v b + m + e 0 , v a + e 1 ) m o d q ℓ . \mathbf{c} = (\beta, \alpha) = v(b,a) + (m + e_0, e_1) \mod q_\ell =(vb+m + e_0,va+e_1)\mod q_\ell. c=(β,α)=v(b,a)+(m+e0,e1)modqℓ=(vb+m+e0,va+e1)modqℓ. -
解密: 输入私钥 s k = ( 1 , s ) sk = (1, s) sk=(1,s)和密文 c ∈ R q ℓ 2 \mathbf{c} \in R_{q_\ell}^2 c∈Rqℓ2,如下计算:
⟨ c , s k ⟩ m o d q ℓ = β + α s m o d q ℓ = v b + m + e 0 + ( v a + e 1 ) s m o d q ℓ = v ( − a s + e ) + m + e 0 + ( v a + e 1 ) s m o d q ℓ = m + v e + e 0 + e 1 s \begin{aligned} &\langle \mathbf{c}, sk \rangle \mod q_\ell \\ & = \beta + \alpha s \mod q_\ell \\ & = vb+m + e_0+(va+e_1)s\mod q_\ell \\ & = v(-as+e)+m + e_0+(va+e_1)s\mod q_\ell \\ & = m +ve+ e_0+e_1s \end{aligned} ⟨c,sk⟩modqℓ=β+αsmodqℓ=vb+m+e0+(va+e1)smodqℓ=v(−as+e)+m+e0+(va+e1)smodqℓ=m+ve+e0+e1s -
标量与密文乘法: 输入标量 k k k和密文 c \mathbf{c} c,直接乘
k c = ( k β , k α ) = k v ( b , a ) + k ( m + e 0 , e 1 ) m o d q ℓ = ( k v b + k m + k e 0 , k v a + k e 1 ) m o d q ℓ . k\mathbf{c} = (k\beta, k\alpha) = kv(b,a) + k(m + e_0, e_1) \mod q_\ell =(kvb+km + ke_0,kva + ke_1)\mod q_\ell. kc=(kβ,kα)=kv(b,a)+k(m+e0,e1)modqℓ=(kvb+km+ke0,kva+ke1)modqℓ. -
解密: ⟨ k c , s k ⟩ m o d q ℓ = k β + k α s m o d q ℓ = k v b + k m + k e 0 + k ( v a + e 1 ) s m o d q ℓ = k v ( − a s + e ) + k m + k e 0 + k ( v a + e 1 ) s m o d q ℓ = k m + k v e + k e 0 + k e 1 s \begin{aligned} &\langle k\mathbf{c}, sk \rangle \mod q_\ell \\ & = k\beta + k\alpha s \mod q_\ell \\ & = kvb+km + ke_0+k(va+e_1)s\mod q_\ell \\ & = kv(-as+e)+km + ke_0+k(va+e_1)s\mod q_\ell \\ & = km +kve+ ke_0+ke_1s \end{aligned} ⟨kc,sk⟩modqℓ=kβ+kαsmodqℓ=kvb+km+ke0+k(va+e1)smodqℓ=kv(−as+e)+km+ke0+k(va+e1)smodqℓ=km+kve+ke0+ke1s
解密获得 k m km km。如果 k = 10000 k=10000 k=10000,则是扩大;如果 k = 1 / 10000 k=1/10000 k=1/10000则是缩小。注意:直接缩小可能会与噪声重叠,解密会出错。通常需要先放大,后缩小,才不会与噪声重叠。 -
同态加法: c + c ′ = ( ( v + v ′ ) b + ( m + m ′ ) + ( e 0 + e 0 ′ ) , ( a + a ′ ) a + ( e 1 + e 1 ′ ) ) m o d q ℓ \mathbf{c} + \mathbf{c}'=((v+v')b+(m+m') + (e_0+e_0'),(a+a')a+(e_1+e_1'))\mod q_\ell c+c′=((v+v′)b+(m+m′)+(e0+e0′),(a+a′)a+(e1+e1′))modqℓ
-
解密:
输入私钥 s k = ( 1 , s ) sk = (1, s) sk=(1,s)和密文 c + c ′ ∈ R q ℓ 2 \mathbf{c} + \mathbf{c}' \in R_{q_\ell}^2 c+c′∈Rqℓ2,如下计算:
⟨ ( c + c ′ ) , s k ⟩ m o d q ℓ = ( β + β ′ ) + ( α + α ′ ) s m o d q ℓ = ( v + v ′ ) b + ( m + m ′ ) + ( e 0 + e 0 ′ ) + ( a + a ′ ) a s + ( e 1 + e 1 ′ ) s m o d q ℓ = ( v + v ′ ) ( − a s + e ) + ( m + m ′ ) + ( e 0 + e 0 ′ ) + ( a + a ′ ) a s + ( e 1 + e 1 ′ ) s m o d q ℓ = ( m + m ′ ) + ( v + v ′ ) e + ( e 0 + e 0 ′ ) + ( e 1 + e 1 ′ ) s \begin{aligned} &\langle (\mathbf{c} + \mathbf{c}'), sk \rangle \mod q_\ell \\ & = (\beta+\beta') + (\alpha+\alpha') s \mod q_\ell \\ & = (v+v')b+(m+m') + (e_0+e_0') + (a+a')as+(e_1+e_1')s\mod q_\ell \\ & = (v+v')(-as+e)+(m+m') + (e_0+e_0') + (a+a')as+(e_1+e_1')s\mod q_\ell \\ & = (m+m') +(v+v')e+ (e_0+e_0')+(e_1+e_1')s \end{aligned} ⟨(c+c′),sk⟩modqℓ=(β+β′)+(α+α′)smodqℓ=(v+v′)b+(m+m′)+(e0+e0′)+(a+a′)as+(e1+e1′)smodqℓ=(v+v′)(−as+e)+(m+m′)+(e0+e0′)+(a+a′)as+(e1+e1′)smodqℓ=(m+m′)+(v+v′)e+(e0+e0′)+(e1+e1′)s -
同态乘法: c ⋅ c ′ = ( β , α ) ( β ′ , α ′ ) = ( β β ′ , β α ′ , α β ′ , α α ′ ) = ( d 0 , d 1 ) + t − 1 d 2 e v k m o d q ℓ , \mathbf{c} \cdot \mathbf{c}' = (\beta, \alpha)(\beta', \alpha') =(\beta\beta',\beta\alpha',\alpha\beta',\alpha\alpha') = (d_0, d_1) + t^{-1} d_2 evk \mod q_\ell, c⋅c′=(β,α)(β′,α′)=(ββ′,βα′,αβ′,αα′)=(d0,d1)+t−1d2evkmodqℓ,
使用密钥交换技术使得扩展密文 c ⋅ c ′ = ( d 0 , d 1 , d 2 ) \mathbf{c} \cdot \mathbf{c}' =(d_0, d_1, d_2) c⋅c′=(d0,d1,d2)变成正常密文 ( β ˉ , α ˉ ) (\bar{\beta}, \bar{\alpha}) (βˉ,αˉ)。 -
解密:
-
如果是扩展密文 c ⋅ c ′ = ( d 0 , d 1 , d 2 ) \mathbf{c} \cdot \mathbf{c}' =(d_0, d_1, d_2) c⋅c′=(d0,d1,d2),则使用扩展私钥 ( 1 , s , s 2 ) (1,s,s^2) (1,s,s2)解密;
-
如果是再线性化密文 ( β ˉ , α ˉ ) (\bar{\beta}, \bar{\alpha}) (βˉ,αˉ),则使用正常私钥 ( 1 , s ) (1, s) (1,s)解密(通常是该情况,使得加密生成的密文与经过同态计算的密文不可区分)。
-
需要注意:当我们有两个密文 c , c ′ \mathbf{c}, \mathbf{c}' c,c′处于不同的级别 ℓ ′ < ℓ \ell' < \ell ℓ′<ℓ 时,应该通过调整更高级别的密文的级别来匹配两个密文的级别,即 ℓ ′ = ℓ \ell' = \ell ℓ′=ℓ。这可以通过重新缩放过程实现,该过程将级别为 ℓ \ell ℓ 的密文 c ∈ R q ℓ 2 \mathbf{c} \in R_{q_\ell}^2 c∈Rqℓ2 转换为 c ′ = ⌊ q ℓ ′ / q ℓ ⌉ m o d q ℓ ′ \mathbf{c}' = \lfloor q_{\ell'} / q_\ell \rceil \mod q_{\ell'} c′=⌊qℓ′/qℓ⌉modqℓ′。
CKKS16特点: 消息空间可以表示为扩展域 C C C中的元素。非正式地,消息 m m m可以嵌入 S = R [ x ] / ⟨ x d + 1 ⟩ S = R[x]/\langle x^d + 1 \rangle S=R[x]/⟨xd+1⟩ 中。由于 x d + 1 x^d + 1 xd+1的根是复数单位根,若要将 m ∈ S m \in S m∈S转换为复数向量,只需在这些复数根上对其进行求值。
第四代方案类似于第二代方案,区别在第四代是近似计算,能用于浮点数计算,且计算速度显著提高。
3.4.2 CKKS16应用
CKKS16实现浮点计算:
1.234 × 0.689 × 2.194 × 0.971 × 3.323 × 4.154 × 0.489 × 3.772 = ? 1.234\times 0.689\times 2.194\times 0.971\times 3.323\times 4.154\times 0.489\times 3.772 =? 1.234×0.689×2.194×0.971×3.323×4.154×0.489×3.772=?
-
ChatGPT 4o: 46.03 46.03 46.03
-
Gork 2.0: 45.8 45.8 45.8
-
deepseek: 46.12 46.12 46.12
逐步计算并保留2位小数: 1.23 × 0.68 × 2.19 × 0.91 × 3.32 × 4.15 × 0.48 × 3.77 = 41.62 1.23 \times 0.68 \times 2.19 \times 0.91 \times 3.32 \times 4.15 \times 0.48 \times 3.77=41.62 1.23×0.68×2.19×0.91×3.32×4.15×0.48×3.77=41.62
逐步计算并保留所有小数: 1.23 ⋅ 0.68 ⋅ 2.19 ⋅ 0.91 ⋅ 3.32 ⋅ 4.15 ⋅ 0.48 ⋅ 3.77 = 41.5594574077313280 ≈ 41.56 1.23\cdot 0.68\cdot 2.19\cdot 0.91\cdot 3.32\cdot 4.15\cdot 0.48\cdot 3.77 = 41.5594574077313280\approx 41.56 1.23⋅0.68⋅2.19⋅0.91⋅3.32⋅4.15⋅0.48⋅3.77=41.5594574077313280≈41.56
先放大,再缩小: 12340 ⋅ 6890 ⋅ 21940 ⋅ 9170 ⋅ 33230 ⋅ 41540 ⋅ 4890 ⋅ 37720 / 1000 0 8 = 4.361 ⋅ 1 0 33 / 1000 0 8 = 43.61 12340\cdot 6890\cdot 21940\cdot 9170\cdot 33230\cdot 41540\cdot 4890\cdot 37720 / {10000^8}=4.361\cdot {10^{33}}/{10000^8} = 43.61 12340⋅6890⋅21940⋅9170⋅33230⋅41540⋅4890⋅37720/100008=4.361⋅1033/100008=43.61
方法: 先放大,再计算,再缩小最终结果,则能获得准确值。
消息1.234扩大12340,然后加密,然后同态乘法,然后解密,然后缩小10000,获得1.234。加密和解密过程中的噪声对放大的消息影响较小。
缩减技术: CKKS16的密文能够乘以常量 1 / p 1/p 1/p,实现对应明文数据的缩小,用于缩小噪声。

图 9: 近似同态计算
参考文献
-
GGH公钥密码系统 Public-key cryptosystems from lattice reduction problems
-
Regev05论文On Lattices, Learning with Errors, Random Linear Codes, and Cryptography
-
Brakerski12论文Fully Homomorphic Encryption without Modulus Switching from Classical GapSVP
-
Micciancio-Regev书 Lattice-based cryptography
-
KTX07论文Multi-bit Cryptosystems Based on Lattice Problems
-
DGHV10论文Fully homomorphic encryption over the integers
-
LV10论文On Ideal Lattices and Learning with Errors over Rings
-
Gentry09论文Fully homomorphic encryption using ideal lattices
-
CR16论文Recovering Short Generators of Principal Ideals in Cyclotomic Rings
-
BV11论文Efficient Fully Homomorphic Encryption from (Standard)LWE
-
LTV13论文On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption
-
GSW13论文Homomorphic Encryption from Learning with Errors:Conceptually-Simpler, Asymptotically-Faster, Attribute-Based
-
TRLWE18论文TFHE: Fast Fully Homomorphic Encryption over the Torus
-
陈智罡 全同态加密:从理论到实践
-
周福才、徐剑 格理论与密码学
-
Google Jeremy Kun 2024.5博客 A High-Level Technical Overview of Fully Homomorphic Encryption
-
Optalysys团队2024年10月博客 Fully Homomorphic Encryption industry leaders join forces to form global FHE Hardware Consortium
-
Fhenix团队2023年10月17日博客 The Holy Grail of Encryption: The Rise of FHE Technology
-
NGC Ventures团队2024年1月12日博客 Introduction to FHE and Blockchain: Implications for Scalability and Privacy
-
Awesome Fully Homomorphic Encryption (FHE) x Blockchain resources, libraries, projects, and more
-
Awesome Homomorphic Encryption
-
PANews 2024年9月17日文章 全同态加密(FHE)的进展与应用
-
2022年论文《Survey on Fully Homomorphic Encryption, Theory, and Applications》
-
Craig Gentry 2022年论文《Homomorphic encryption: a mathematical survey》
-
2024年12月20日Jorge Myszne,Niobium Microsystems 首席产品官 博客 3 Homomorphic Encryption Trends for 2025
-
HCLTech团队2024年6月研报 Homomorphic encryption: Exploring technology trends and future approach
-
2024年论文《vFHE: Verifiable Fully Homomorphic Encryption》
-
PPS Lab团队2023年10月博客 Arithmetizing FHE in Circom
-
PPS Lab团队2023年10月博客 A primer on the FHEW & TFHE schemes
-
2024年论文《Oraqle: A Depth-Aware Secure Computation Compiler》
-
2023年10月论文《A Survey on Implementations of Homomorphic Encryption Schemes》
-
Sunscreen团队2021年8月博客 An Intro to Fully Homomorphic Encryption for Engineers
-
TFHE:2016年论文《Faster Fully Homomorphic Encryption: Bootstrapping in less than 0.1 Seconds》
-
BGV:2011年论文 《Fully Homomorphic Encryption without Bootstrapping》
-
BFV:2012年论文《Somewhat Practical Fully Homomorphic Encryption》
-
CKKS:2016年论文《Homomorphic Encryption for Arithmetic of Approximate Numbers》
-
HomomorphicEncryption.org 2018年slide Building Applications with Homomorphic Encryption
-
Greenfield Capital 2024年7月博客 The muted Seven – 7 things you should consider re confidential compute
-
Sunscreen 2023年8月博客 How SNARKs fall short for FHE
-
2024年4月18日BigBrainVC团队博客 Flawed Homomorphic Encryption
-
2024年Verisense Network slide An Introduction To FHE and Its Application in Rust
-
Vitalik 2020年7月20日博客 Exploring Fully Homomorphic Encryption
-
2023年论文《Verifiable Fully Homomorphic Encryption》
-
2018年《Homomorphic Encryption Standard v1.1》
-
2021年论文《SoK: Fully Homomorphic Encryption Compilers》
-
2024年论文《SoK: Fully Homomorphic Encryption Accelerators》
-
Sunscreen团队2023年5月博客 Building an FHE compiler for the real world
-
Zama团队2023年5月23日博客 Private Smart Contracts Using Homomorphic Encryption
-
Craig Gentry 2024年6月分享视频 FHE: Past, Present and Future
相关文章:

全同态加密理论、生态现状与未来展望(中2)
《全同态加密理论、生态现状与未来展望》系列由lynndell2010gmail.com和mutourend2010gmail.com整理原创发布,分为上中下三个系列: 全同态加密理论、生态现状与未来展望(上):专注于介绍全同态加密理论知识。全同态加密…...
鸿蒙UI(ArkUI-方舟UI框架)-开发布局
返回主章节 → 鸿蒙UI(ArkUI-方舟UI框架) 开发布局 1、布局概述 1)布局结构 2)布局元素组成 3)如何选择布局 声明式UI提供了以下10种常见布局,开发者可根据实际应用场景选择合适的布局进行页面开发。 …...
RPC是什么?和HTTP区别?
RPC 是什么?HTTP 是什么? 作为一个程序员,假设我们需要从A电脑的进程发送一段数据到B电脑的进程,我们一般会在代码中使用 Socket 进行编程。 此时,可选性一般就是 TCP 和 UDP 二选一,由于 TCP 可靠、UDP 不…...

Linux C\C++编程-建立文件和内存映射
【图书推荐】《Linux C与C一线开发实践(第2版)》_linux c与c一线开发实践pdf-CSDN博客 《Linux C与C一线开发实践(第2版)(Linux技术丛书)》(朱文伟,李建英)【摘要 书评 试读】- 京东图书 Linu…...
行政纠错——pycorrector学习
pycorrector是一个开源中文文本纠错工具,它支持对中文文本进行音似、形似和语法错误的纠正。此工具是使用Python3进行开发的,并整合了Kenlm、ConvSeq2Seq、BERT、MacBERT、ELECTRA、ERNIE、Transformer等多种模型来实现文本纠错功能。pycorrector官方仓库…...

Go的defer原理
Go 的 defer 原理 defer 是 Go 语言中的一个关键字,用于延迟执行一个函数调用。它通常用于处理资源释放、连接关闭等操作,确保这些操作在函数返回之前执行。 1. 什么是 defer? defer 关键字用于延迟执行一个函数调用,直到包含它…...

Windows 下本地 Docker RAGFlow 部署指南
Windows 下本地 Docker RAGFlow 部署指南 环境要求部署步骤1. 克隆代码仓库2. 配置 Docker 镜像加速(可选)3. 修改端口配置(可选)4. 启动服务5. 验证服务状态6. 访问服务7. 登录系统8. 配置模型8.1 使用 Ollama 本地模型8.2 使用在线 API 服务9. 开始使用10. 常见问题处理端…...

专题三_穷举vs暴搜vs深搜vs回溯vs剪枝_全排列
dfs解决 全排列&子集 1.全排列 link:46. 全排列 - 力扣(LeetCode) 全局变量回溯 code class Solution { public:vector<vector<int>> ans;vector<int> cur;vector<bool> used;vector<vector<int>> permute…...

【IEEE Fellow 主讲报告| EI检索稳定】第五届机器学习与智能系统工程国际学术会议(MLISE 2025)
重要信息 会议时间地点:2025年6月13-15日 中国深圳 会议官网:http://mlise.org EI Compendex/Scopus稳定检索 会议简介 第五届机器学习与智能系统工程国际学术会议将于6月13-15日在中国深圳隆重召开。本次会议旨在搭建一个顶尖的学术交流平台…...

华为E9000刀箱服务器监控指标解读
美信监控易内置了数千种常见设备监测器,能够监测超过20万项指标。这些指标涵盖了从硬件设备到软件系统,从网络性能到安全状态等各个方面。如下基于美信监控易——IT基础监控模块,对华为E9000刀箱服务器部分监控指标进行解读。 一、华为E9000…...

【LC】2544. 交替数字和
题目描述: 给你一个正整数 n 。n 中的每一位数字都会按下述规则分配一个符号: 最高有效位 上的数字分配到 正 号。剩余每位上数字的符号都与其相邻数字相反。 返回所有数字及其对应符号的和。 示例 1: 输入:n 521 输出&…...
QT QTreeWidget控件 全面详解
本系列文章全面的介绍了QT中的57种控件的使用方法以及示例,包括 Button(PushButton、toolButton、radioButton、checkBox、commandLinkButton、buttonBox)、Layouts(verticalLayout、horizontalLayout、gridLayout、formLayout)、Spacers(verticalSpacer、horizontalSpacer)、…...
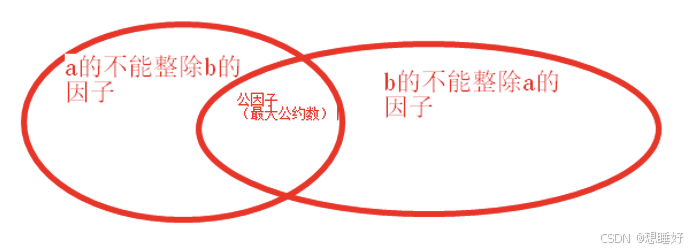
欧几里得算法求最小公倍数和最大公约数
一.最大公约数 gcd(a,b)gcd(b,a%b) 递归式,当且仅当b0,易得0和a的公约数为a.(可作为递归的出口) 证明: int gcd(int a, int b) {if (b 0) return a;else return gcd(b, a % b); } 二.最小公倍数 给定整数a b,求a b的最小公倍数 有图可知…...

Selenium配合Cookies实现网页免登录
文章目录 前言1 方案一:使用Chrome用户数据目录2 方案二:手动获取并保存Cookies,后续使用保存的Cookies3 注意事项 前言 在进行使用Selenium进行爬虫、网页自动化操作时,登录往往是一个必须解决的问题,但是Selenium每次…...
DeepSeek R1模型解读与使用
字节在春节前发布了doubao-1.5,它的官方介绍竟然是这样的: 这次发布了四个型号,doubao-1.5-pro-32k, doubao-1.5-pro-256k, doubao-1.5-lite-32k, doubao-1.5-vision-pro-32k,价格全部与上一个版本doubao模型一致,加量…...

Windows电脑不小心点击了关机,关机过程中如何阻止
如果电脑正在关机的过程中,想要阻止关机,可以尝试以下方法: 如果关机过程较慢,可以按下键盘组合键 Win R 打开运行窗口。输入 shutdown -a 后按回车键,这将中断关机操作(适用于 Windows 系统)…...
CNN-GRU卷积门控循环单元时间序列预测(Matlab完整源码和数据)
CNN-GRU卷积门控循环单元时间序列预测(Matlab完整源码和数据) 目录 CNN-GRU卷积门控循环单元时间序列预测(Matlab完整源码和数据)预测效果基本介绍CNN-GRU卷积门控循环单元时间序列预测一、引言1.1、研究背景与意义1.2、研究现状1…...

【吉林乡镇界】面图层shp格式arcgis数据乡镇名称和编码wgs84无偏移内容测评
标题中的“吉林省乡镇界面图层shp格式arcgis数据乡镇名称和编码wgs84无偏移”揭示了这是一个地理信息系统(GIS)相关的数据集,主要用于描绘吉林省的乡镇边界。这个数据集包含了一系列的文件,它们是ArcGIS软件能够识别和处理的Shape…...

fpga学习入门 串口rs232回环
奇偶检验位这里是省略了 做好回环后可以使用上位机做回环测试,top文件写的方式就是将rx(fpga端)接受到的模块(pc端)tx发送出去,这两个端口用杜邦线连接,同理模块的rx连接fpga的tx,…...

智启未来,AI筑梦科技新星”------华清远见成都中心2025冬令营圆满结束
2025年1月11日-16日,华清远见成都中心为期6天的“智启未来,AI筑梦科技新星”2025冬令营活动圆满结束。此次活动吸引了众多对人工智能和无人驾驶技术充满热情的学生参与,共同开启了一段点燃科技梦想的精彩旅程。 报道接待 以AI无人驾驶小车为核…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
