蓝桥杯 阶乘的和(C++完整代码+详细分析)
题目描述
原题链接
阶乘的和
问题描述
给定 n 个数 Ai,问能满足 m! 为 ∑=(Ai!) 的因数的最大的 m 是多少。其中 m! 表示 m 的阶乘,即 1×2×3×⋯×m。
输入格式
输入的第一行包含一个整数 n。
第二行包含 n 个整数,分别表示 Ai,相邻整数之间使用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
样例输入
3
2 2 2
样例输出
3
题目分析
要点1:阶乘之和的因数
n个不同的阶乘Ai 之和的最大因数(可写成m!)即为n个阶乘中的那个最小的阶乘。
例如,
3个阶乘: 2 ! 4 ! 3 ! 2! 4! 3! 2!4!3!
之和为 2 ∗ 1 + 4 ∗ 3 ∗ 2 ∗ 1 + 3 ∗ 2 ∗ 1 = 32 2*1+4*3*2*1+3*2*1=32 2∗1+4∗3∗2∗1+3∗2∗1=32,
能作其因数的阶乘的最大值即为 2 ! 2! 2!
因为,要想做阶乘之和的因数,则一定是各个阶乘的因数,则最大因数一定为最小的那个阶乘。
要点2:阶乘之和的转化
i + 1 i+1 i+1 个 i ! i! i! 可转化为 ( i + 1 ) ! (i+1)! (i+1)!
例如,
3 3 3 个 2 ! 2! 2! 为 3 ∗ 2 ! = 3 ! 3*2!=3! 3∗2!=3!
因为,
i + 1 i+1 i+1 个 i ! i! i!为 ( i + 1 ) ∗ i ! = ( i + 1 ) ! (i+1)*i!=(i+1)! (i+1)∗i!=(i+1)!
整体分析
则我们可以记录数据中最小的阶乘 res ,
以及各个阶乘出现的次数(便于进行阶乘的转化)
scanf("%d",&n);unordered_map<int,int> map; //map记录Ai阶乘的次数int res=2e9; //res为阶乘的最小值,设定初值为无穷大for(int i=0;i<n;i++){int a; //阶乘a!scanf("%d",&a);map[a]++; //阶乘a!出现次数+1res=min(res,a); //找到Ai中的最小值res}
从阶乘数最小的res开始遍历阶乘,
若满足 m a p [ i ] % ( i + 1 ) = = 0 map[i]\%(i+1)==0 map[i]%(i+1)==0,
则说明存在 i + 1 i+1 i+1 个 i ! i! i! ,可转化为 ( i + 1 ) ! (i+1)! (i+1)!,
且可转为 ( i + 1 ) ! (i+1)! (i+1)!的个数为 m a p [ i ] / ( i + 1 ) map[i]/(i+1) map[i]/(i+1).
否则,
更新阶乘失败,不存在更大的阶乘因数,退出循环遍历。
for(int i=res;;i++){if(map[i]%(i+1)==0){ //有i+1个i!,则可转化为(i+1)!res=i+1; //答案更新为i+1map[i+1]+=map[i]/(i+1); //由i!转化为map[i]/(i+1)个(i+1)!}else break; //退出循环}
完整代码
#include <iostream>
#include <unordered_map>
#include <algorithm>
using namespace std;
int n;
int main()
{scanf("%d",&n);unordered_map<int,int> map; //map记录Ai阶乘的次数int res=2e9; //res为结果,设定初值为无穷大for(int i=0;i<n;i++){int a; //阶乘a!scanf("%d",&a);map[a]++; //阶乘出现次数+1res=min(res,a); //找到Ai中的最小值}for(int i=res;;i++){if(map[i]%(i+1)==0){ //有i+1个i!,则可转化为(i+1)!res=i+1; //答案更新为i+1map[i+1]+=map[i]/(i+1); //由i!转化为map[i]/(i+1)个(i+1)!}else break;}printf("%d",res);return 0;
}
相关文章:
)
蓝桥杯 阶乘的和(C++完整代码+详细分析)
题目描述 原题链接 阶乘的和 问题描述 给定 n 个数 Ai,问能满足 m! 为 ∑(Ai!) 的因数的最大的 m 是多少。其中 m! 表示 m 的阶乘,即 123⋯m。 输入格式 输入的第一行包含一个整数 n。 第二行包含 n 个整数,分别表示 Ai,相…...
【Bug 记录】el-sub-menu 第一次进入默认不高亮
项目场景: 项目场景:el-sub-menu 第一次进入默认不高亮 问题描述 例如:sub-menu 的 index 后端默认传过来是 number,我们需要手动转为 string,否则会有警告,而且第一次进入 sub-menu 默认不高亮。 解决方…...

SpringCloud两种注册中心
SpringCloud 基本概念 系统架构 我们之前做的所有的项目都属于单体架构,下面我们将要学习更适合大型项目的分布式架构 单体架构: 将业务的所有功能几种在一个项目中开发,打成一个包部署。 优点:架构简单、部署成本低 缺点&am…...

陕西羊肉泡馍:味蕾上的西北风情
陕西羊肉泡馍:味蕾上的西北风情 在广袤的西北地区,有一道美食以其独特的口感、丰富的营养价值和深厚的文化底蕴,成为了无数食客心中的佳肴——陕西羊肉泡馍。这道传统美食,不仅承载着陕西人民的饮食智慧,更以其醇厚的味道和暖胃耐饥的特性,赢得了国内外食客的一致赞誉。 历史渊…...

蓝桥杯试题:整数反转
一、题目要求: 给定一个整数,请将该数各个位上数字反转得到一个新数。新数也应满足整数的常见形式,即除非给定的原数为零,否则反转后得到的新数的最高位数字不应为零 二、题目分析代码演示: 该程序的主要功能是接收一个整数输入&…...
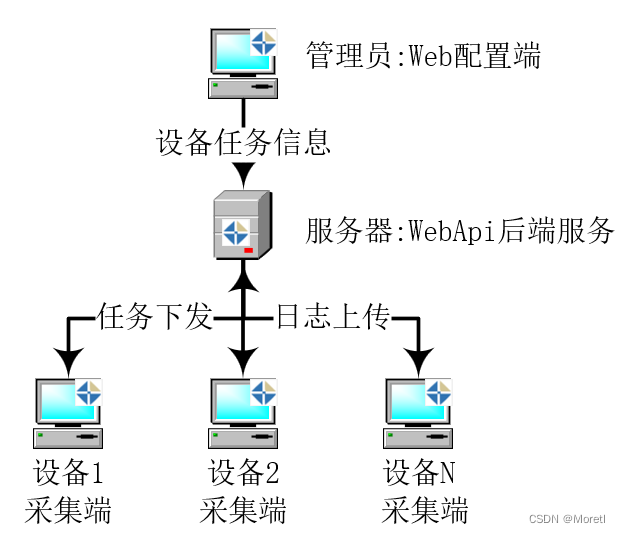
Moretl FileSync增量文件采集工具
永久免费: <下载> <使用说明> 我们希望Moretl FileSync是一款通用性很好的文件日志采集工具,解决工厂环境下,通过共享目录采集文件,SMB协议存在的安全性,兼容性的问题. 同时,我们发现工厂设备日志一般为增量,为方便MES,QMS等后端系统直接使用数据,我们推出了增量采…...
day1代码练习
输出3-100以内的完美数,(完美数:因子和(因子不包含自身)数本身) #include <stdio.h>// 判断一个数是否为完美数的函数 int panduan(int n) {if (n < 2) {return 0; // 小于2的数不可能是完美数}int sum 1; // 因子和初始化为1(因…...

【Pytest】结构介绍
1.目录结构介绍 project_root/ │ ├── tests/ # 测试用例存放目录 │ ├── __init__.py │ ├── test_module1.py │ ├── module1.py # 被测试的模块 ├── conftest.py # pytest配置文件,可定义fixture和钩子函数 ├── py…...

Django基础之ORM
一.前言 上一节简单的讲了一下orm,主要还是做个了解,这一节将和大家介绍更加细致的orm,以及他们的用法,到最后再和大家说一下cookie和session,就结束了全部的django基础部分 二.orm的基本操作 1.settings.py&#x…...

【以音频软件FFmpeg为例】通过Python脚本将软件路径添加到Windows系统环境变量中的实现与原理分析
在Windows系统中,你可以通过修改环境变量 PATH 来使得 ffmpeg.exe 可在任意路径下直接使用。要通过Python修改环境变量并立即生效,如图: 你可以使用以下代码: import os import winreg as reg# ffmpeg.exe的路径 ffmpeg_path …...

检测到联想鼠标自动调出运行窗口,鼠标自己作为键盘操作
联想鼠标会自动时不时的调用“运行”窗口 然后鼠标自己作为键盘输入 然后打开这个网页 (不是点击了什么鼠标外加按键,这个鼠标除了左右和中间滚轮,没有其他按键了)...

web UI自动化测试笔记
在当今数字化转型的浪潮中,Web 应用已经无处不在,而其质量保障的关键之一就是自动化测试。想象一下,如果每次都手动验证 UI 功能,不仅耗时耗力,还容易遗漏问题。Python 的强大生态为 Web UI 自动化测试提供了高效的解决…...

计算机网络 (60)蜂窝移动通信网
一、定义与原理 蜂窝移动通信网是指将一个服务区分为若干蜂窝状相邻小区并采用频率空间复用技术的移动通信网。其原理在于,将移动通信服务区划分成许多以正六边形为基本几何图形的覆盖区域,称为蜂窝小区。每个小区设置一个基站,负责本小区内移…...

计算机网络三张表(ARP表、MAC表、路由表)总结
参考: 网络三张表:ARP表, MAC表, 路由表,实现你的网络自由!!_mac表、arp表、路由表-CSDN博客 网络中的三张表:ARP表、MAC表、路由表 首先要明确一件事,如果一个主机要发送数据,那么必…...

DRF开发避坑指南01
在当今快速发展的Web开发领域,Django REST Framework(DRF)以其强大的功能和灵活性成为了众多开发者的首选。然而,错误的使用方法不仅会导致项目进度延误,还可能影响性能和安全性。本文将从我个人本身遇到的相关坑来给大…...

批量提取多个 Excel 文件内指定单元格的数据
这篇文章将介绍如何从多个相同格式的Excel文件中,批量提取指定单元格的数据,合并后保存到新的工作薄。 全程0代码,可视化操作。 提取前: 提取后: 准备数据 这里准备了3个测试数据 开始提取 打开的卢易表࿰…...

#HarmonyOS篇:build-profile.json5里面配置productsoh-package.json5里面dependencies依赖引入
oh-package.json5 用于描述包名、版本、入口文件和依赖项等信息。 {"license": "","devDependencies": {},"author": "","name": "entry","description": "Please describe the basic…...

Spring集成Redis|通用Redis工具类
一、基础使用 概述 在SpringBoot中一般使用RedisTemplate提供的方法来操作Redis。那么使用SpringBoot整合Redis需要 那些步骤呢。 1、 JedisPoolConfig (这个是配置连接池) 2、 RedisConnectionFactory 这个是配置连接信息,这里的RedisConnectionFactory是一个接 …...

Vue中设置报错页面和“Uncaught runtime errors”弹窗关闭
文章目录 前言操作步骤大纲1.使用Vue自带的报错捕获机制添加报错信息2.在接口报错部分添加相同机制3.把报错信息添加到Vuex中方便全局使用4.添加报错页面备用5.app页面添加if判断替换报错界面 效果备注:vue项目中Uncaught runtime errors:怎样关闭 前言 在开发Vue项…...

【力扣】219. 存在重复元素 II
题目 给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] nums[j] 且 abs(i - j) < k 。如果存在,返回 true ;否则,返回 false 。 示例 1: 输入:…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...
