【算法学习】归并排序算法思想的应用—求逆序对数量
Hey,大家好!👋 今天我们来聊聊一个有趣的话题——如何在归并排序的基础上,高效解决求逆序对数量的问题。如果你对算法感兴趣,或者正在准备算法面试,这篇文章一定会对你有所帮助!🚀
题目描述 📝
给定一个长度为 n 的整数数列,请你计算数列中的逆序对的数量。
逆序对的定义如下:
对于数列的第 i 个和第 j 个元素,如果满足 i < j 且 a[i] > a[j],则其为一个逆序对;否则不是。
输入格式
第一行包含整数 n,表示数列的长度。
第二行包含 n 个整数,表示整个数列。
输出格式
输出一个整数,表示逆序对的个数。
数据范围
1 ≤ n ≤ 100000,数列中的元素的取值范围 [1,10^9]。
输入样例:
6
2 3 4 5 6 1
输出样例:
5
理解何为逆序对 🤔
首先,我们来理解一下什么是逆序对。简单来说,逆序对就是在一个数列中,前面的数比后面的数大。比如在数列 [2, 3, 4, 5, 6, 1] 中,2 和 1 就是一个逆序对,因为 2 > 1 且 2 在 1 的前面。
解题策略 🛠️
1. 策略①:暴力解决 💪
算法思路
在理解了逆序对的概念之后,很自然能想到可以直接使用逐个比较的策略进行求解:
分别将每个元素和其后面的所有元素进行
逐个比较
- if 后面有比其小的元素: 逆序对数量++
- 重复直至最后一个元素
核心代码
// 暴力解决策略的核心代码
int count = 0;
for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {if (a[i] > a[j]) {count++;}}
}
复杂度分析
需要使用两个for循环—— O ( n 2 ) O(n^2) O(n2)
复杂度较高,在一些要求较高的情况下会报超时错误
小挑战:你能尝试用暴力解法解决这个问题吗?试试看,感受一下它的时间复杂度吧!😉
2. 策略②:运用「归并排序」的算法思想 🧠
(1)回顾「归并排序」算法原理
归并排序是一种经典的分治算法,它的核心思想是将一个数组分成两个子数组,分别对子数组进行排序,然后将两个有序的子数组合并成一个有序的数组。归并排序的时间复杂度是 O ( n log n ) O(n \log n) O(nlogn),比暴力解法高效得多。
(2)改动以求逆序对数量
原理分析
在归并排序的过程中,当我们合并两个有序的子数组时,如果左边的某个元素 a[i] 大于右边的某个元素 a[j],那么 a[i] 和 a[j] 就构成了一个逆序对。不仅如此,由于左边的子数组是有序的,a[i] 后面的所有元素也都大于 a[j],因此我们可以一次性计算出多个逆序对。
代码实现
#include <iostream>using namespace std;typedef long long LL; // 结果较大const int N = 100010;
int n;
int a[N], temp[N];// 求逆序对数量
LL rev_pair(int a[], int l, int r)
{if (l >= r)return 0;int mid = l + r >> 1;LL res = rev_pair(a, l, mid) + rev_pair(a, mid + 1, r);int i = l, j = mid + 1;int k = 0;while (i <= mid && j <= r){if (a[i] <= a[j])temp[k++] = a[i++];else{temp[k++] = a[j++];// 当a[i]>a[j]时,对于a[j]:与[i, mid]区间内的元素可组成逆序对res += mid - i + 1;}}while (i <= mid)temp[k++] = a[i++];while (j <= r)temp[k++] = a[j++];for (int i = l, j = 0; i <= r; ++i, ++j)a[i] = temp[j];return res;
}int main()
{cin >> n;for (int i = 0; i < n; ++i)cin >> a[i];LL res = rev_pair(a, 0, n - 1);cout << res << endl;return 0;
}
复杂度分析
归并排序的时间复杂度是 O ( n log n ) O(n \log n) O(nlogn),因此这个解法的时间复杂度也是 O ( n log n ) O(n \log n) O(nlogn),比暴力解法高效得多。
学习建议和鼓励 🌟
- 多动手实践:算法的学习离不开实践,建议你亲自编写代码并运行,感受算法的魅力。
- 不要害怕挑战:算法的学习过程中难免会遇到困难,但每一次克服困难都是一次成长。💪
- 多与他人交流:加入一些算法学习群,和志同道合的小伙伴一起讨论问题,互相学习。
互动性元素 🎉
小挑战:你能尝试用归并排序的思想解决其他问题吗?比如求一个数组中的顺序对数量?🤔
推荐阅读:如果你对归并排序还不熟悉,推荐你阅读这篇关于「归并排序」的博客,里面有详细的归并排序讲解。
结语 🎯
通过这篇文章,我们不仅学习了如何用归并排序的思想高效解决求逆序对数量的问题,还了解了暴力解法和优化解法之间的差异。希望你能从中有所收获,并在算法的学习道路上越走越远!🚀
如果你有任何问题或想法,欢迎在评论区留言,我们一起讨论!😄
Happy Coding! 🎉
相关文章:

【算法学习】归并排序算法思想的应用—求逆序对数量
Hey,大家好!👋 今天我们来聊聊一个有趣的话题——如何在归并排序的基础上,高效解决求逆序对数量的问题。如果你对算法感兴趣,或者正在准备算法面试,这篇文章一定会对你有所帮助!🚀 …...

一组开源、免费、Metro风格的 WPF UI 控件库
前言 今天大姚给大家分享一个开源、免费、Metro风格的 WPF UI 控件库:MahApps.Metro。 项目介绍 MahApps.Metro 是一个开源、免费、Metro风格的 WPF UI 控件库,提供了现代化、平滑和美观的控件和样式,帮助开发人员轻松创建具有现代感的 Win…...

Spring Security 应用详解
Spring Security 应用详解 集成SpringBootSpring Boot 介绍创建maven工程spring 容器配置Servlet Context配置安全配置测试 工作原理结构总览认证流程认证流程AuthenticationProviderUserDetailsServicePasswordEncoder 授权流程授权流程授权决策 自定义认证自定义登录页面认证…...

业务对象和对象的区别
"业务对象"和"对象"这两个术语在日常编程和软件工程中经常被使用,但它们之间存在一些区别,主要体现在它们的目的、范围和抽象层次上。 ### 对象(Object) 1. **定义**: - 对象是面向对象编程&#…...

81,【5】BUUCTF WEB [b01lers2020]Life on Mars
进入靶场 怎莫颠颠的,一下子就想到展博了 先把左边的挨个点一遍 在最后一个有点收获 不过也没其他收获了 这种进去给个正常网页的题目,基本都靠url获取信息了 抓包看看有没有其他信息 竟然没有任何信息 自闭了 看别人的wp去咯 为什么别人抓到的包里…...

华硕笔记本装win10哪个版本好用分析_华硕笔记本装win10专业版图文教程
华硕笔记本装win10哪个版本好用?华硕笔记本还是建议安装win10专业版。Win分为多个版本,其中家庭版(Home)和专业版(Pro)是用户选择最多的两个版本。win10专业版在功能以及安全性方面有着明显的优势ÿ…...

Linux进程 -fork(初识),进程状态和进程优先级
目录 一、通过系统调用创建进程-fork 1.fork的介绍 2.fork的理解 3.fork常规用法 4.fork的三个问题 5.创建多个子进程 二、进程状态 (1)Linux内核源代码 (2)进程的状态 R运行状态(运行态) S 睡眠状态&…...

数据从前端传到后端入库过程分析
数据从前端传到后端入库过程分析 概述 积累了一些项目经验,成长为一个老程序员了,自认为对各种业务和技术都能得心应手的应对了,殊不知很多时候我们借助了搜索引擎的能力,当然现在大家都是通过AI来武装自己。 今天要分析的话题是…...

macOS如何进入 Application Support 目录(cd: string not in pwd: Application)
错误信息 cd: string not in pwd: Application 表示在当前目录下找不到名为 Application Support 的目录。可能的原因如下: 拼写错误或路径错误:确保你输入的目录名称正确。目录名称是区分大小写的,因此请确保使用正确的大小写。正确的目录名…...

第38周:猫狗识别 (Tensorflow实战第八周)
目录 前言 一、前期工作 1.1 设置GPU 1.2 导入数据 输出 二、数据预处理 2.1 加载数据 2.2 再次检查数据 2.3 配置数据集 2.4 可视化数据 三、构建VGG-16网络 3.1 VGG-16网络介绍 3.2 搭建VGG-16模型 四、编译 五、训练模型 六、模型评估 七、预测 总结 前言…...

【2024年华为OD机试】 (A卷,200分)- 计算网络信号、信号强度(JavaScriptJava PythonC/C++)
一、问题描述 题目解析 问题描述 我们有一个 m x n 的二维网格地图,每个格子可能是以下几种情况之一: 0:表示该位置是空旷的。x(正整数):表示该位置是信号源,信号强度为 x。-1:表示该位置是阻隔物,信号无法直接穿透。信号源只有一个,阻隔物可能有多个。信号在传播…...

【go语言】数组和切片
一、数组 1.1 什么是数组 数组是一组数:数组需要是相同类型的数据的集合;数组是需要定义大小的;数组一旦定义了大小是不可以改变的。 1.2 数组的声明 数组和其他变量定义没有什么区别,唯一的就是这个是一组数,需要给…...

2025美赛MCM数学建模A题:《石头台阶的“记忆”:如何用数学揭开历史的足迹》(全网最全思路+模型)
✨个人主页欢迎您的访问 ✨期待您的三连 ✨ 《石头台阶的“记忆”:如何用数学揭开历史的足迹》 目录 《石头台阶的“记忆”:如何用数学揭开历史的足迹》 ✨摘要✨ ✨引言✨ 1. 引言的结构 2. 撰写步骤 (1)研究背景 &#…...

使用 Docker Compose 一键启动 Redis、MySQL 和 RabbitMQ
目录 一、Docker Compose 简介 二、服务配置详解 1. Redis 配置 2. MySQL 配置 3. RabbitMQ 配置 三、数据持久化与时间同步 四、部署与管理 五、总结 目录挂载与卷映射的区别 现代软件开发中,微服务架构因其灵活性和可扩展性而备受青睐。为了支持微服务的…...

新增自定义数据功能|UWA Gears V1.0.7
UWA Gears 是UWA最新发布的无SDK性能分析工具。针对移动平台,提供了实时监测和截帧分析功能,帮助您精准定位性能热点,提升应用的整体表现。 本次版本更新新增了自定义数据功能,支持灵活定义和捕获关键性能指标,满足特…...
docker 简要笔记
文章目录 一、前提内容1、docker 环境准备2、docker-compose 环境准备3、流程说明 二、打包 docker 镜像1、基础镜像2、国内镜像源3、基础的dockerfile4、打包镜像 四、构建运行1、docker 部分2、docker-compose 部分2.1、构建docker-compose.yml2.1.1、同目录构建2.1.2、利用镜…...

在Ubuntu上使用Apache+MariaDB安装部署Nextcloud并修改默认存储路径
一、前言 Nextcloud 是一款开源的私有云存储解决方案,允许用户轻松搭建自己的云服务。它不仅支持文件存储和共享,还提供了日历、联系人、任务管理、笔记等丰富的功能。本文将详细介绍如何在 Ubuntu 22.04 LTS 上使用 Apache 和 MariaDB 安装部署 Nextcl…...
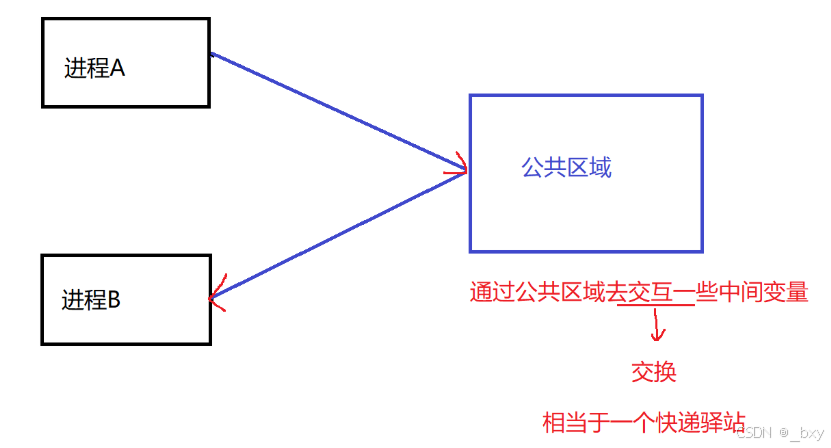
【JavaEE】-- 计算机是如何工作的
文章目录 1. 冯诺依曼体系(VonNeumann Architecture)2. CPU 基本工作流程2.1 寄存器(Register)和 内存(RAM)2.2 控制单元 CU(ControlUnit)2.3 指令(Instruction) 3. 操作系统(OperatingSystem)3.1 操作系统的定位3.2 什么是进程/任务(Process…...
政安晨的AI大模型训练实践三:熟悉一下LF训练模型的WebUI
政安晨的个人主页:政安晨 欢迎 👍点赞✍评论⭐收藏 希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正! 目录 启动WebUI 微调模型 LLaMA-Factory 支持通过 WebUI 零代码微调大语言模型。 启动Web…...
基于微信小程序的网上订餐管理系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、Vue项目源码、SSM项目源码、微信小程序源码 精品专栏:…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
