高等数学学习笔记 ☞ 微分方程
1. 微分方程的基本概念
1. 微分方程的基本概念:
(1)微分方程:含有未知函数及其导数或微分的方程。
举例说明微分方程:
;
。
(2)微分方程的阶:指微分方程中未知函数的导数的最高阶数。
举例说明微分方程的阶数:一阶微分方程:
,
;二阶微分方程:
,
。
(3)微分方程的解:就是把一个函数代入微分方程使其成立,那么这个函数就是微分方程的解。
(4)微分方程的通解:它是微分方程的解,该解具有《解里边含有任意常数的个数等于微分方程的阶数》特性。
举例说明微分方程的通解:
;
。
(5)微分方程的特解:将给定的初始条件代入微分方程的通解,求解任意常数后的通解,称为微分方程的特解。
举例说明微分方程的特解:已知初始条件:
,微分方程
的通解为:
,
将初始条件代入通解,可得:
,则特解为
。
(6)解微分方程:就是找出未知函数的过程。
2. 微分方程的分类:
(1)根据微分方程中所含有的自变量的个数分类:
①:常微分方程:指微分方程中只包含一个自变量的方程,如:。
②:偏微分方程:指微分方程中包含两个或两个以上自变量的方程,如:。
备注:偏微分方程里边含有偏导数,如
。
(2)根据微分方程中未知函数及其导数之间的关系分类:
①:线性微分方程:指未知函数及其导数呈线性关系。如:。
②:非线性微分方程:指未知函数及其导数不呈线性关系。如;
。
备注:微分方程的线性与非线性与线性代数中的线性与非线性是有区别的。
2. 一阶微分方程
2.1 可分离变量的微分方程
1. 定义:就是指自变量和因变量可以分离开来的微分方程。可转化为形如类型的等式。
说明:①:
:与
相关的式子;
:与
相关的式子。
②:等式两端同时取不定积分,即:
,再进一步进行求解即可。
2. 举例说明:
(1)求微分方程的通解:
解:等式两端同时取不定积分,可得:
。
求解等式两端的不定积分可得:
。
等式两端同时取
的指数,整理得:
。
进一步整理可得:
。
备注:求解微分方程时,根据实际情况适当的对
进行处理,如
。
(2)求微分方程的通解:
解:方程两端同时除以
,然后等式两端同时取不定积分,可得:
。
求解等式两端的不定积分可得:
。
进一步整理可得微分方程的解:
。
注意:当最等式两端做除法运算时,需要考虑相应的定义(验证通解是否包含特殊情况),即:
当同时除以
时,默认是
的,那么此时就需要验证
是否是
微分方程的解。将
代入微分方程可知,等式成立,故
也是微分方程的解。
备注:求解微分方程时不要漏解,一般要求最终整理出来的式子不要带分式。
2.2 齐次微分方程
1. 定义:就是指自变量和因变量作为一个整体出现且次数相等的微分方程。可转化为形如或
类型的等式。
说明:
表明:
是自变量和
是因变量;
表明:
是自变量和
是因变量。
2. 举例说明:
(1)求微分方程的通解(固定解法,三步走):
解:方程两端同时除以
,整理可得:
。①
三步走:令
,则
。②
②带入①上式可得:
。
对上式方程两端同时取不定积分并整理可得:
。
进行回代可得:
。
(2)求微分方程的通解(固定解法,三步走):
解:三步走:令
,则
。
将上式带入微分方程可得:
。
对上式方程两端同时取不定积分并整理可得:
。
进行回代可得:
。
2.3 一阶线性微分方程
1. 定义:就是指未知函数的导数的最高阶数为1且未知函数及其导数之间呈线性关系的微分方程,
可转化为形如或
类型的等式。
备注:当
与
出现在一起时,默认意识都是
是关于
的函数,但其实
也是关于
的函数。
2. 种类:
(1)一阶齐次线性微分方程:指或
时的一阶线性微分方程。
求解方法:转化为可分离变量的微分方程的形式进行求解。
(2)一阶非齐次线性微分方程:指或
时的一阶线性微分方程。
求解方法:
第一步:将原微分方程转化为
或
的标准形式,
并明确
与
或
与
的表达式。
第二步:直接带入通解公式:
或
。
3. 举例说明:
(1)求微分方程的通解:
解:根据微分方程可知:
。
带入通解公式可得:
注意:求解一阶非齐次线性微分方程时,常数
只需要在最后那一项添加即可。
(2)求微分方程的通解:
解:根据微分方程可知:
。
带入通解公式可得:
注意:求解一阶非齐次线性微分方程时,若
的指数幂含有
或
形式的不定积分,则积出来的原函数不用加绝对值。
2.4 伯努利方程
1. 定义:形如的微分方程。
2. 求解过程:
第一步:等式两端同时除以,可得:
。
第二步:将拿到导数部分,可得:
。
第三步:令,并整理可得:
。
第四步:将看成一个整体,
看成一个整体,即转化为一阶线性微分方程。
第五步:按照一阶线性微分方程的求解方法,求解完微分方程后进行的回代。
3. 举例说明:求微分方程的通解:
解:根据微分方程可知:
,则
。
将
带入原微分方程可得:
。
由上式可得:
。
所以:
。
将
回代可得:
。
3. 高阶微分方程
3.1 可降阶的高阶微分方程
1. 形如:型的微分方程
例:求微分方程的通解。
解:对微分方程连续积分两次可得:
,
。
备注:
型微分方程的通解含有
个任意常数(微分方程的阶数)。
2. 形如:型的微分方程
例:求微分方程的通解。
解:设,则
,代入原微分方程可得:
。
对两端同时取积分可得:
。
又知,则有
。
对连续积分3次可得:
。
备注:替换后得到的一阶微分方程的形式不同,根据相应的形式去求解。
3. 形如:型的微分方程
例:求微分方程的通解。
解:设,则
,代入原微分方程可得:
。
对两端同时取积分可得:
。
又知,则有
。
对同时取积分可得:
。
核心思想:设
,即:
,则
,即:
。
3.2 二阶常系数齐次线性微分方程
1. 二阶齐次线性微分方程:形如的微分方程。
2. 二阶齐次线性微分方程解的结构:
(1)若,
是
的解,则
也是
的解。
备注:按照微分方程的解的定义即可求证。
但不一定是
的通解。
。
备注:按照微分方程的通解的定义即可求证。
那么如何保证是
的通解呢?
想要保证是通解,那么通解必须含有两个任意常数,即这两个常数不会被整合成一个常数。
此时,就需要保证,
不能成比例,也就是保证
,
是线性无关的。
所以:若,
是
的两个线性无关的解,那么
就是
的通解。(定理)
(2)若,
,
是
阶齐次线性微分方程的
个线性无关的解,那么
阶齐次线性微分方程的通解为
。
3. 二阶常系数齐次线性微分方程:形如的微分方程。
4. 二阶常系数齐次线性微分方程求解:
若求的通解,只需要求解出该微分方程的两个线性无关的解,那么根据相关定理,通解就可以表示为:
。故当前目标就是求解出该微分方程的两个线性无关的解。
假设(
为常数)为
的解,但到底是不是该微分方程的解谁知道呢,需要进一步验证。
根据可得:
,
。将其代入
,整理可得:
。
因为,故若使得
恒成立,则有:
成立。
由此可知,只需要解算出的值,并带入
,就可以得到
的解
,故
是微分方程
的解。
此时,我们将称为微分方程
的特征方程。并通过求解特征方程
的特征根
获取微分方程 的两个线性无关的解。分析如下:
特征方程是一个一元二次方程,它的根有以下三种情形:
(1)特征方程有两个不相等的实根,即
。
经过上述分析可知,是微分方程的解,所以我们就直接找到了微分方程的两个解,即
,
。
因为不是成比例关系的,故
与
线性无关。
所以微分方程的通解为:
。
举例说明,求微分方程
的通解:
解:根据所给的微分方程可得:特征方程
。
解得:
。
所以通解为:
(2)特征方程有两个相等的实根,即
。
经过上述分析可知,是微分方程的解,所以我们就直接找到了微分方程的第一个解,即
。
接下来寻找第二个解,第二个解只需要与第一个解线性无关即可。
因为不能成比例关系,所以设
,即:
。
假设是
的解,但到底是不是该微分方程的解谁知道呢,需要进一步验证。
根据可得:
,
。
将其代入,整理可得:
。
因为是特征方程
的根,则有
。
又因为特征方程有两个相等的实根,则特征方程可表示为
,
通过等式对比可知:。
故。
我们的目的是寻找一个,使得
不成比例,所以根据
,可选取
。
所以微分方程的第二个解为。
因为不是成比例关系的,故
与
线性无关。
所以微分方程的通解为:
。
举例说明,求微分方程
的通解:
解:根据所给的微分方程可得:特征方程
。
解得:
。
所以通解为:
。
(3)特征方程有一对共轭复根,即
,
。
经过上述分析可知,是微分方程的解,所以我们就直接找到了微分方程的两个解,即
,
。
代入整理可得: ,
,此时的解为复数形式,为得到实数形式的解,为此进一步将其转化。
利用欧拉公式:可以把
,
改写为:
,
。
因为微分方程的两个解,则
,
依然是微分方程的两个解(代入证明可得结果),
即:,
。
因为不是成比例关系的,故
与
线性无关。
所以微分方程的通解为:
。
举例说明,求微分方程
的通解:
解:根据所给的微分方程可得:特征方程
。
解得:
。故:
。
所以通解为:
。
5. 阶常系数齐次线性微分方程求解:
| 特征方程的根 | 微分方程通解中的对应项 |
| 单实根 | 给出一项: |
| 一对单复根 | 给出两项: |
| 给出 | |
| 一对 | 给出 |
举例说明:若微分方程的特征根别
,
,
,
。
则通解为:

。
3.3 二阶常系数非齐次线性微分方程
1. 二阶非齐次线性微分方程:形如的微分方程。
2. 二阶非齐次线性微分方程解的结构:
(1)若是
的特解,
是
的通解,
则:的通解为
。
(2)若,
是
的特解,则:
是
的特解。
(3)若是
的特解,
是
的特解,
则:是
的特解。
3. 二阶常系数非齐次线性微分方程:形如的微分方程。
4. 二阶常系数非齐次线性微分方程求解:
由二阶非齐次线性微分方程解的结构可知:
二阶常系数非齐次线性微分方程的通解等于二阶常系数非齐次线性微分方程的特解 + 对应的二阶常系数齐次线性微分方程的通解,
上一节已解决二阶常系数齐次线性微分方程的通解的求法,此时需要解决的问题就是求二阶常系数非齐次线性微分方程的特解。
以下是微分方程中的
取两种常见形式时特解的求法。
(1)型
备注:
是常数;
是关于
的一个
次多项式。
观察可知,等号右边是多项式与指数函数的乘积。而多项式与指数函数的乘积的导数依然是多项式
与指数函数的乘积,所以我们有理由怀疑可能是微分方程的特解。其中
是某个多项式。
假设是微分方程的特解,则
,
。
将,
带入
可得如下等式:
。
根据可得对应的
的特征方程为:
。
①:若不是特征方程
的根,则有
。
因为是关于
的一个
次多项式,若使得
式恒成立,则等号左端也应该是关于
的一个
次多项式,由于
求导
之后,次数降低,所以此时只能是关于
的一个
次多项式。
设,将
带入
式,利用待定系数法,即可得到
的值。所以此时微分方程的特解为:
。
②:若是特征方程
的单根,则有
,
。
因为是关于
的一个
次多项式,若使得
式恒成立,则等号左端也应该是关于
的一个
次多项式,由于
的系数
为零,所以此时只能是关于
的一个
次多项式,那么
则是关于
的一个
次多项式。
设,那么
可用
来表示,将
带入式,利用待定系数法,即可得到
的值。所以此时微分方程的特解为:
。
③:若是特征方程
的重根,则有
,
。
因为是关于
的一个
次多项式,若使得
式恒成立,则等号左端也应该是关于
的一个
次多项式,由于
和
的系数为零,所以此时只能是关于
的一个
次多项式,则
是关于
的一个
次多项式。
设,那么
可用
来表示,将
带入式,利用待定系数法,即可得到
的值。所以此时微分方程的特解为:
。
综上所述,总结如下:
如果
,那么二阶常系数非齐次线性微分方程的特解可以表示为:
。
其中:
与
是同次(
次)的多项式。
不是特征方程的根,则
;
是特征方程的单根,则
,
是特征方程的重根,则
。
(2)型
备注:
是常数;
分别是关于
的一个
次、
次多项式,且有一个多项式可以为零。
如果,那么二阶常系数非齐次线性微分方程的特解可以表示为:
。
其中:与
是
次的多项式
,
,
。
(或
)不是特征方程的根,则
;
(或
)是特征方程的单根,则
。
备注:根据题设写出特解,将其代入原微分方程,利用待定系数法即可求解多项式系数。
相关文章:
高等数学学习笔记 ☞ 微分方程
1. 微分方程的基本概念 1. 微分方程的基本概念: (1)微分方程:含有未知函数及其导数或微分的方程。 举例说明微分方程:;。 (2)微分方程的阶:指微分方程中未知函数的导数…...

【探索 Kali Linux】渗透测试与网络安全的终极操作系统
探索 Kali Linux:渗透测试与网络安全的终极操作系统 在网络安全领域,Kali Linux 无疑是最受欢迎的操作系统之一。无论是专业的渗透测试人员、安全研究人员,还是对网络安全感兴趣的初学者,Kali Linux 都提供了强大的工具和灵活的环…...

四方连续贴图是什么意思
上下左右四个方向都是连续的图案,是由一个纹样或几个纹样组成一个单位,向四周重复地连续和延伸扩展而成的图案形式...

RKNN_C++版本-YOLOV5
1.背景 为了实现低延时,所以开始看看C版本的rknn的使用,确实有不足的地方,请指正(代码借鉴了rk官方的仓库文件)。 2.基本的操作流程 1.读取模型初始化 // 设置基本信息 // 在postprocess.h文件中定义,详见…...

k8s优雅重启
理论上处于terminating状态的pod,k8s 就会把它从service中移除了,只用配置一个优雅停机时长就行了。kubectl get endpoints 验证 因此,优雅重新的核心问题,是怎么让空闲长连接关闭,再等待处理中的请求执行完。 一些底…...

三高“高性能、高并发、高可靠”系统架构设计系列文章
目录 高并发系统的艺术:如何在流量洪峰中游刃有余 《数据密集型应用系统设计》读后感与高并发高性能实践案例 系统稳定性与高可用保障的几种思路 软件系统限流的底层原理解析 技术解决方案调研 延迟队列调研 重试调研 异步回调调研 分库分表调研 分布式事…...

opengrok_使用技巧
Searchhttps://xrefandroid.com/android-15.0.0_r1/https://xrefandroid.com/android-15.0.0_r1/ 选择搜索的目录(工程) 手动在下拉框中选择,或者 使用下面三个快捷按钮进行选择或者取消选择。 输入搜索的条件 搜索域说明 域 fullSearc…...

C++资料
InterviewGuide 首页 - 八股精 Releases halfrost/LeetCode-Go GitHub GitHub - GrindGold/CppGuide: 「C/C学习面试指南」一份涵盖大部分 C 程序员所需要掌握的知识。入门、进阶、深入、校招、社招,准备 C 学习& 面试,首选 CppGuide࿰…...

基于模糊PID的孵化箱温度控制系统(论文+源码)
1系统方案设计 本课题为基于模糊PID的孵化箱温度控制系统,其以STM32最小系统与模糊PID控制器为控制核心。系统主要包括数据采集模块、处理器模块、电机控制模块。 数据采集模块由温度传感器构成,通过温度传感器感应温度变化,获得待处理的数据…...

景联文科技加入AIIA联盟数据标注分委会
2025年1月16日,中国人工智能产业发展联盟(简称AIIA)数据委员会数据标注分委会(以下简称“分委会”)正式成立。景联文科技成为第一批AIIA联盟数据标注分委会委员单位。 数据标注分委会的成立旨在搭建数据标注领域产学研…...

1-1 飞机大战项目框架搭建
前言: 基于本人巩固C语言编写,仅供学习参考 1.0 框架搭建 搭建完成后状态 C语言飞机大战框架 使用loadimage时出现波浪线的错误如何解决,这个问题主要是编码格式不对造成的,我们需要修改系统的编码格式,将unicode编码格…...

【C++高并发服务器WebServer】-7:共享内存
本文目录 一、共享内存1.1 shmget函数1.2 shmat1.3 shmdt1.4 shmctl1.5 ftok1.6 共享内存和内存映射的关联1.7 小demo 二、共享内存操作命令 一、共享内存 共享内存允许两个或者多个进程共享物理内存的同一块区域(通常被称为段)。由于一个共享内存段会称…...

RabbitMQ 多种安装模式
文章目录 前言一、Windows 安装 RabbitMq1、版本关系2、Erlang2.1、下载安装 Erlang 23.12.2、配置 Erlang 环境变量 3、RabbitMQ3.1、下载安装 RabbitMQ 3.8.93.2、环境变量3.3、启动RabbitMQ 管理插件3.3、RabbitMQ3.4、注意事项 二、安装docker1、更新系统包:2、…...

C++ 包装器与绑定器的应用之回调函数的实现
回调函数的实现 在消息队列和网络库的框架中,当接收到消息(报文)时,回调用户自定义的函数对象,把消息(报文)参数传给它,由它决定如何处理。 queue参考文章:C queue(STL queue&…...

Baichuan大模型Base、Chat、Instruct等版本的区别
Baichuan大模型Base与Instruct等版本的区别解析 Baichuan大模型作为国内领先的开源语言模型,其不同版本(如Base、Chat、Instruct等)在训练目标、应用场景和性能特点上存在显著差异。以下是基于公开技术文档和行业分析的详细对比:…...

3.DrawCall的概念
DrawCall是渲染管线中的一个重要概念,指的是CPU向GPU发送的一个绘制命令,告诉GPU:“请根据我提供的数据,画一个物体(或一部分物体)。” 通俗易懂讲解:DrawCall就像给画师下订单 想象你是一个老…...

ubuntu电脑调用摄像头拍摄照片
一、 1、先装环境 conda create -n text python3.8 -y conda activate text 2、 pip install opencv-python -i https://pypi.tuna.tsinghua.edu.cn/simple 1、连接摄像头拍摄收集数据集 capture_image5.py import cv2 as cv import os import datetime import n…...

PyQt4 的图片切割编辑器
一、 编辑器功能明确 允许用户加载图片、选择切割模式、对切割后的图片片段进行操作(如移动、复制、粘贴、删除等),并支持撤销和重做操作。 环境:Py2.7 PyQt 4.11 二、导入模块介绍 sys: 用于访问与 Python 解释器强相关的变…...

mac 电脑上安装adb命令
在Mac下配置android adb命令环境,配置方式如下: 1、下载并安装IDE (android studio) Android Studio官网下载链接 详细的安装连接请参考 Mac 安装Android studio 2、配置环境 在安装完成之后,将android的adb工具所在…...
 - Windows 编译)
Webrtc (1) - Windows 编译
最近项目上遇到webrtc wgc 的几个test case无法通过,与webrtc人员沟通后决定要自行修复一下(因为他们不想管…) 参考文档 https://webrtc.org/support/contributinghttps://chromium.googlesource.com/chromium/src//main/docs/#checking-out-and-building 以上两…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...
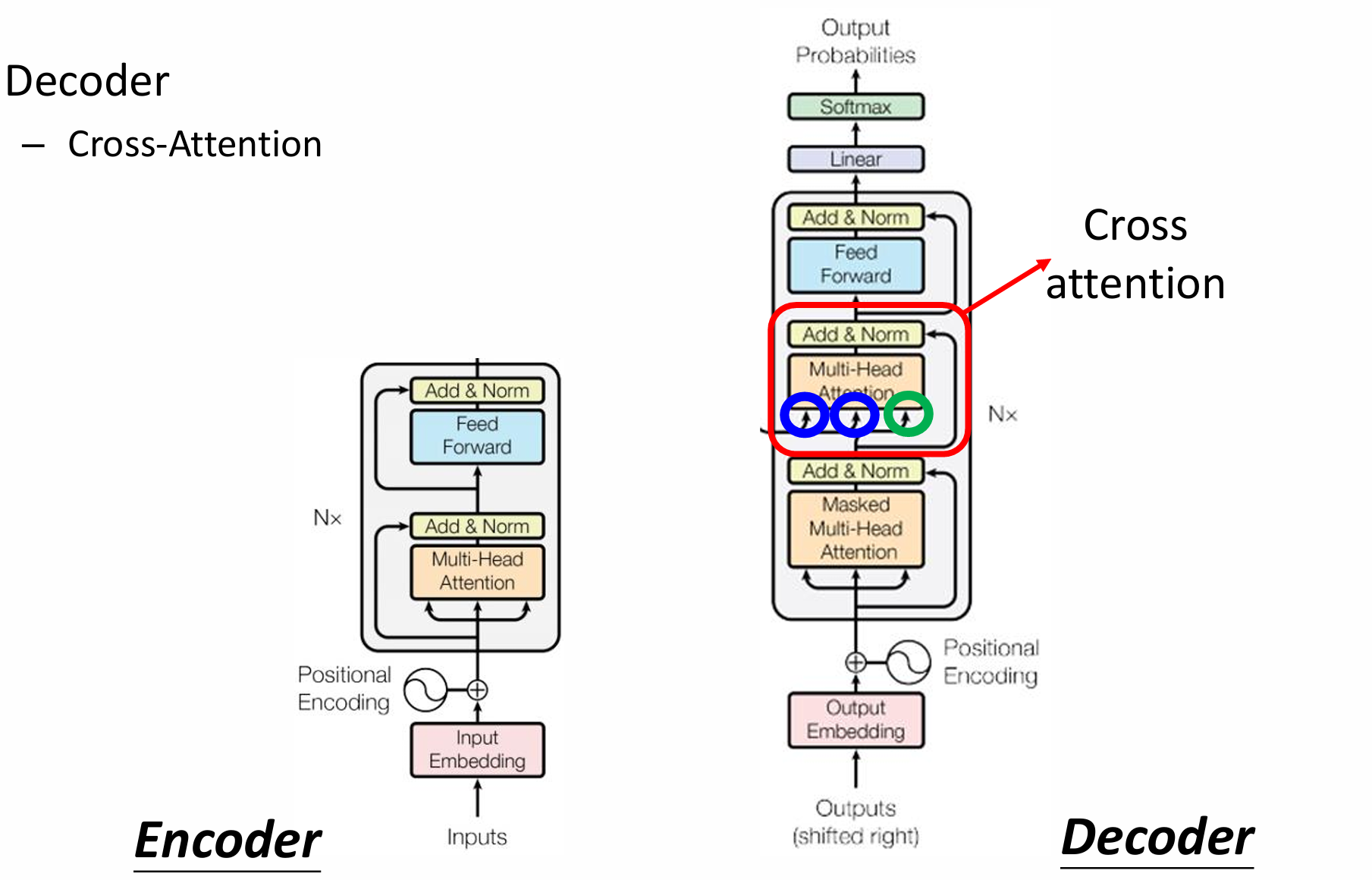
自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
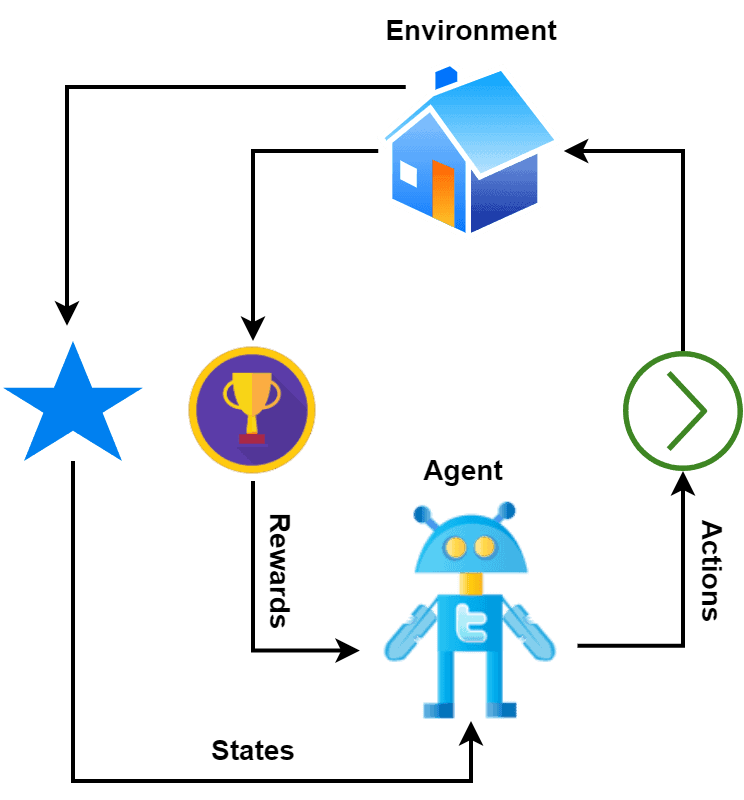
【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
