算法题(56):旋转链表


审题:
我们需要根据k的大小把链表向右移动对应次数,并返回移动后的链表的头结点指针
思路:
根据提示中的数据大小我们发现:k的值可以远大于节点数。也就是说我们对链表的操作存在周期,如果k%len==0,说明我们就不用做任何操作了,而如果k%len!=0,我们需要操作的次数就是运算后的余数。
第一步:确定需要操作的次数
(1)写个getlen方法
(2)利用k=k%len求出需要操作的次数k
实际上,我们如果真的一次次去操作链表会发现一个问题:我们如何更新指针?
因为每次进行移动我们都需要头指针,尾指针
问题出在尾指针又需要我们每次都去遍历一次链表来找。
那么我们有没有办法可以只进行一次操作呢?
我们只需要找到移动k次后的头结点,该头结点的前一个节点,以及一开始的链表的尾结点即可
第二步:找到三个关键节点
第三步:修改指针指向
最后是特殊情况处理
解题:
(1)确定需要操作的次数
getlen的逻辑就是遍历链表,每次遍历到一个节点就让num++,直到遍历到空指针
特殊情况处理:
1.当链表为空的时候len为0,由于0不能做被除数,所以这里k%0会出问题,我们要提前截断这种情况
2.当k取余后为0,说明不用我们操作,直接返回head
(2)找到三个关键节点
疑问:为什么prvleft需要指向一个哨兵节点?
若他指向head先,而我们的left最终也是head,就会因为逻辑问题出错
(3)修改指针指向
61. 旋转链表 - 力扣(LeetCode)
相关文章:

算法题(56):旋转链表
审题: 我们需要根据k的大小把链表向右移动对应次数,并返回移动后的链表的头结点指针 思路: 根据提示中的数据大小我们发现:k的值可以远大于节点数。 也就是说我们对链表的操作存在周期,如果k%len0,说明我们…...

解决PyG安装中torch-sparse安装失败问题:详细指南
1 问题描述 最近在学习GNN,需要使用PyTorch Geometric(PyG)库。在安装PyG的过程中,遇到了torch-sparse安装失败的问题,错误提示为: ERROR: Failed building wheel for torch-sparse本文将详细记录问题的解…...

如何创建折叠式Title
文章目录 1 概念介绍2 使用方法3 示例代码 我们在上一章回中介绍了SliverGrid组件相关的内容,本章回中将介绍SliverAppBar组件.闲话休提,让我们一起Talk Flutter吧。 1 概念介绍 我们在本章回中介绍的SliverAppBar和普通的AppBar类似,它们的…...

go-zero学习笔记(三)
利用goctl生成rpc服务 编写proto文件 // 声明 proto 使用的语法版本 syntax "proto3";// proto 包名 package demoRpc;// golang 包名(可选) option go_package "./demo";// 如需为 .proto 文件添加注释,请使用 C/C 样式的 // 和 /* ... */…...

Wildcard工具详解:从入门到精通
1. Wildcard基础知识 什么是Wildcard? Wildcard(通配符)是一种用于匹配文件名或字符串的特殊字符。它允许用户使用简单的符号来表示复杂的匹配规则,从而快速定位目标文件或数据。 常见的Wildcard符号 *:匹配任意数量…...

冰蝎v3.0 beta7来啦
我用了一台kali,一台centos,一台windows,做了一个文件上传和一个反弹shell实验,载荷是AES加密的,终于感受到了对加密流量的无可奈何~ kali(php8.1)centos(php7.1)window…...

React中使用箭头函数定义事件处理程序
React中使用箭头函数定义事件处理程序 为什么使用箭头函数?1. 传递动态参数2. 避免闭包问题3. 确保每个方块的事件处理程序是独立的4. 代码可读性和维护性 示例代码总结 在React开发中,处理事件是一个常见的任务。特别是当我们需要传递动态参数时&#x…...

记忆化搜索和动态规划 --最长回文子串为例
记忆化搜索 记忆化搜索是一种优化递归算法的方法,通过将已经计算过的子问题的结果存储起来(通常使用哈希表或数组),避免重复计算相同的子问题。 本质上是通过缓存中间结果来减少计算的重复性。 动态规划 动态规划是通过将问题分…...
 ))
Tree Compass( Codeforces Round 934 (Div. 2) )
Tree Compass( Codeforces Round 934 (Div. 2) ) You are given a tree with n n n vertices numbered 1 , 2 , … , n 1, 2, \ldots, n 1,2,…,n. Initially, all vertices are colored white. You can perform the following two-step operation: …...

【Numpy核心编程攻略:Python数据处理、分析详解与科学计算】2.17 掩码数组:缺失值处理的优雅方案
2.17 掩码数组:缺失值处理的优雅方案 目录 #mermaid-svg-12vjJJbyudPnkYBO {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-12vjJJbyudPnkYBO .error-icon{fill:#552222;}#mermaid-svg-12vjJJbyudPnkYBO…...

PHP 常用函数2025.02
PHP implode() 函数 语法 implode(separator,array) 参数描述separator可选。规定数组元素之间放置的内容。默认是 ""(空字符串)。array必需。要组合为字符串的数组。 技术细节 返回值:返回一个由数组元素组合成的字符串。PHP 版…...

react中如何获取dom元素
实现代码 const inputRef useRef(null) inputRef.current.focus()...

【C++】继承(下)
大家好,我是苏貝,本篇博客带大家了解C的继承(下),如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 5.继承与友元6.继承与静态成员7.复杂的菱形继承及菱形虚拟继承8.继…...

C语言实现字符串排序:从代码到原理深度解析
在编程的世界里,字符串处理是一项基础且重要的技能。今天,我们通过分析一段C语言代码来深入了解如何对字符串进行排序。 一、代码呈现 #include <stdio.h> #include <string.h> int main() { char s[1001]; scanf("%s", s); int…...

Vue3的el-table-column下拉输入实时查询API数据选择的实现方法
由于本人对el-table-column有下拉输入选择的要求,根据网上搜索的资料及本人优化,推出我比较满意的方法,供各位读者参考使用。 效果图 el-table-column写法 <el-table-columnlabel"货品编号"align"center"prop"…...
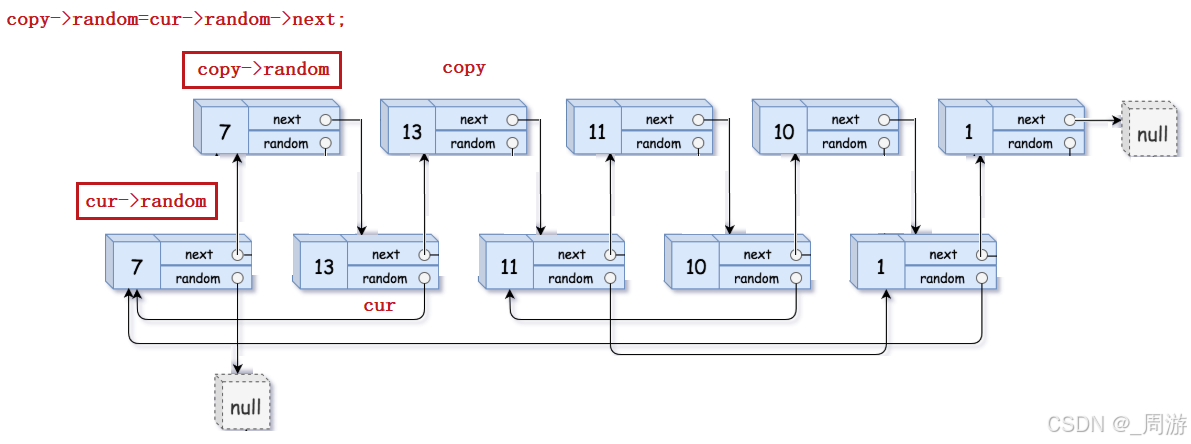
【数据结构】_链表经典算法OJ:复杂链表的复制
目录 1. 题目链接及描述 2. 解题思路 3. 程序 1. 题目链接及描述 题目链接:138. 随机链表的复制 - 力扣(LeetCode) 题目描述: 给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,…...

Vue 图片引用方式详解:静态资源与动态路径访问
目录 前言1. 引用 public/ 目录2. assets/ 目录3. 远程服务器4. Vue Router 动态访问5. 总结6. 扩展(图片不显示) 前言 🤟 找工作,来万码优才:👉 #小程序://万码优才/r6rqmzDaXpYkJZF 在 Vue 开发中&#x…...

chatGPT写的网页版贪吃蛇小游戏
chatGPT写的网页版贪吃蛇小游戏 前言网页版贪吃蛇小游戏 前言 之前无聊,让ChatGPT写了一段基于html语言的贪吃蛇小游戏代码 网页版贪吃蛇小游戏 将以下内容复制到记事本,重命名为xxx.html即可打开浏览器游玩 这里是一个使用HTML、CSS和JavaScript编写…...

Python量化交易助手:xtquant的安装与应用
Python量化交易助手:xtquant的安装与应用 技术背景和应用场景 在量化交易领域,Python因其强大的库支持和灵活性成为了许多开发者的首选语言。其中,xtquant 是迅投官方开发的一个Python包,专门用于与miniqmt通信,实现…...

前缀和算法
文章目录 算法总览题目1371.每个元音包含偶数次的最长子字符串 算法总览 题目 1371.每个元音包含偶数次的最长子字符串 1371.每个元音包含偶数次的最长子字符串 参考博主的讲解 思路分析:就是得使用前缀和记录情况,dp[i][j]表示s[0] 到s[i] 中&…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...




