第二十章 存储函数
目录
一、概述
二、语法
三、示例
一、概述
前面章节中,我们详细讲解了MySQL中的存储过程,掌握了存储过程之后,学习存储函数则肥仓简单,存储函数其实是一种特殊的存储过程,也就是有返回值的存储过程。存储函数的参数只能是IN类型的。
二、语法
CREATE FUNCTION 存储函数名称 ([ 参数列表 ])
RETURNS type [characteristic ...]
BEGIN
-- SQL语句
RETURN ...;
END ;characteristic说明:
DETERMINISTIC:相同的输入参数总是产生相同的结果
NO SQL :不包含 SQL 语句。
READS SQL DATA:包含读取数据的语句,但不包含写入数据的语句。
三、示例
计算从1累加到n的值,n为传入的参数值。
create function fun1(n int)
returns int deterministic
begindeclare total int default 0;while n > 0 doset total := total + n;set n := n - 1;end while;return total;
end;select fun1(50);在mysql8.0版本中binlog默认是开启的,一旦开启了,mysql就要求在定义存储过程时,需要指定
characteristic特性,否则就会报如下错误:

相关文章:

第二十章 存储函数
目录 一、概述 二、语法 三、示例 一、概述 前面章节中,我们详细讲解了MySQL中的存储过程,掌握了存储过程之后,学习存储函数则肥仓简单,存储函数其实是一种特殊的存储过程,也就是有返回值的存储过程。存储函数的参数…...

架构规划之任务边界划分过程中承接分配
架构师在边界划分的过程中需要做什么事情呢?接下来,我们会讨论一些关于任务分配的 基础假设,以及由这些基础假设而带来的决策路径。 所谓任务边界划分,就是判定某个任务在多个承接方中,应该归属到哪个承接方的过程。…...

【C++】线程池实现
目录 一、线程池简介线程池的核心组件实现步骤 二、C11实现线程池源码 三、线程池源码解析1. 成员变量2. 构造函数2.1 线程初始化2.2 工作线程逻辑 3. 任务提交(enqueue方法)3.1 方法签名3.2 任务封装3.3 任务入队 4. 析构函数4.1 停机控制 5. 关键技术点解析5.1 完美转发实现5…...

vsnprintf的概念和使用案例
vsnprintf 是 C/C 标准库中用于格式化字符串的安全函数,属于 <stdio.h>(C)或 <cstdio>(C)头文件。它是 snprintf 的可变参数版本(v 表示 va_list),允许通过 va_list 处理…...

解读隐私保护工具 Fluidkey:如何畅游链上世界而不暴露地址?
作者:Techub 独家解读 撰文:Tia,Techub News 隐私不只是个人权利的象征,更是我们迈向透明、信任未来的重要过渡桥梁。如果你还未意识到隐私的重要性,推荐阅读 KeyMapDAO 的文章《「被出卖的自由」:我到底该…...

Linux环境Kanass安装配置简明教程
Kanass是一款国产开源免费的项目管理软件,本文将介绍如何快速在linux centos环境下安装配置,以快速上手。 1. 安装 以下以linux centos7下安装为例。 下载,下载地址:Kanass - 下载,下载Linux安装包如tiklab-kanass-1.0.4.rpm&am…...

数据分析常用的AI工具
数据分析领域中常用的AI工具种类繁多,涵盖了从数据处理、分析到可视化和预测的各个环节。以下是一些常见且广泛应用的AI数据分析工具及其特点: 1. 数据处理与清洗工具 Python库:如PandasAI,集成了生成式AI能力,支持自…...

项目中常用中间件有哪些?分别起什么作用?
在项目开发中,常用的中间件包括消息中间件、缓存中间件、数据库中间件等,以下是一些常见的中间件及其作用: 消息中间件 Kafka:一般用于处理大规模的消息数据,具有高吞吐量、低延迟的特点,适用于日志收集、…...

kaggle视频行为分析1st and Future - Player Contact Detection
这次比赛的目标是检测美式橄榄球NFL比赛中球员经历的外部接触。您将使用视频和球员追踪数据来识别发生接触的时刻,以帮助提高球员的安全。两种接触,一种是人与人的,另一种是人与地面,不包括脚底和地面的,跟我之前做的这…...

1. junit5介绍
JUnit 5 是 Java 生态中最流行的单元测试框架,由 JUnit Platform、JUnit Jupiter 和 JUnit Vintage 三个子项目组成。以下是 JUnit 5 的全面使用指南及示例: 一、环境配置 1. Maven 依赖 <dependency><groupId>org.junit.jupiter</grou…...

(脚本学习)BUU18 [CISCN2019 华北赛区 Day2 Web1]Hack World1
自用 题目 考虑是不是布尔盲注,如何测试:用"1^1^11 1^0^10,就像是真真真等于真,真假真等于假"这个测试 SQL布尔盲注脚本1 import requestsurl "http://8e4a9bf2-c055-4680-91fd-5b969ebc209e.node5.buuoj.cn…...

Caxa 二次开发 ObjectCRX-1 踩坑:环境配置以及 Helloworld
绝了,坑是真 nm 的多,官方给的文档里到处都是坑。 用的环境 ObjectCRX,以下简称 objcrx。 #1 安装环境 & 参考文档的大坑 #1.1 Caxa 提供的文档和环境安装包 首先一定要跟 Caxa 对应版本的帮助里提供的 ObjectCRX 安装器 (wizard) 匹配…...

【自然语言处理(NLP)】生成词向量:GloVe(Global Vectors for Word Representation)原理及应用
文章目录 介绍GloVe 介绍核心思想共现矩阵1. 共现矩阵的定义2. 共现概率矩阵的定义3. 共现概率矩阵的意义4. 共现概率矩阵的构建步骤5. 共现概率矩阵的应用6. 示例7. 优缺点优点缺点 **总结** 目标函数训练过程使用预训练的GloVe词向量 优点应用总结 个人主页:道友老…...

bable-预设
babel 有多种预设,最常见的预设是 babel/preset-env,它可以让你使用最新的 JS 语法,而无需针对每种语法转换设置具体的插件。 babel/preset-env 预设 安装 npm i -D babel/preset-env配置 .babelrc 文件 在根目录下新建 .babelrc 文件&a…...

回顾生化之父三上真司的游戏思想
1. 放养式野蛮成长路线,开创生存恐怖类型 三上进入capcom后,没有培训,没有师傅手把手的指导,而是每天摸索写策划书,老员工给出不行的评语后,扔掉旧的重写新的。 然后突然就成为游戏总监,进入开…...

无公网IP 外网访问青龙面板
青龙面板是一款基于 Docker 的自动化管理平台,用户可以通过简便的 Web 界面,轻松的添加、管理和监控各种自动化任务。而且这款面板还支持多用户、多任务、任务依赖和日志监控,个人和团队都比较适合使用。 本文将详细的介绍如何用 Docker 在本…...

中国证券基本知识汇总
中国证券市场是一个多层次、多领域的市场,涉及到各种金融工具、交易方式、市场参与者等内容。以下是中国证券基本知识的汇总: 1. 证券市场概述 证券市场:是指买卖证券(如股票、债券、基金等)的市场。证券市场可以分为…...

C基础寒假练习(2)
一、输出3-100以内的完美数,(完美数:因子和(因子不包含自身)数本身 #include <stdio.h>// 函数声明 int isPerfectNumber(int num);int main() {printf("3-100以内的完美数有:\n");for (int i 3; i < 100; i){if (isPerfectNumber…...

Baklib如何提升内容中台智能化推荐系统的精准服务与用户体验
内容概要 在数字化转型的浪潮中,内容中台的智能化推荐系统成为提升用户体验的重要工具。Baklib作为行业领先者,在这一领域积极探索,推出了具有前瞻性的解决方案,旨在提高内容的匹配度和推荐的精准性。本文将深入探讨Baklib如何通…...

【Java】位图 布隆过滤器
位图 初识位图 位图, 实际上就是将二进制位作为哈希表的一个个哈希桶的数据结构, 由于二进制位只能表示 0 和 1, 因此通常用于表示数据是否存在. 如下图所示, 这个位图就用于标识 0 ~ 14 中有什么数字存在 可以看到, 我们这里相当于是把下标作为了 key-value 的一员. 但是这…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...
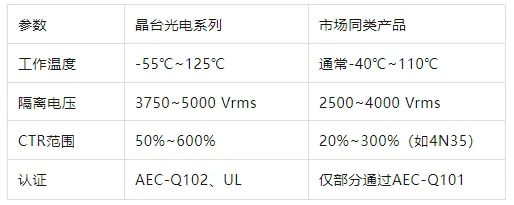
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...
