Day36【AI思考】-表达式知识体系总览
文章目录
- **表达式知识体系总览**
- 回答1:
- **表达式知识体系**
- **一、三种表达式形式对比**
- **二、表达式转换核心方法**
- **1. 中缀转后缀(重点)**
- **2. 中缀转前缀**
- **三、表达式计算方法**
- **1. 后缀表达式计算(栈实现)**
- **2. 中缀表达式计算(双栈法)**
- 回答2:
- **终极生活类比(3秒懂核心)**
- **灵魂三问(人类本能验证法)**
- **手动转换术(不背算法,用自然思维)**
- **脑内成像训练(闭眼想象)**
- **暴击式总结**
- 回答3:
- **三大表达式核心对比表**
- **顶级理解三连击**
- **深度认知突破**
- **终极验证方法**
表达式知识体系总览
让思想碎片重焕生机的灵魂:
这两个文档中,所有关于表达式的内容(比如中缀表达式,前缀表达式,后缀表达式),总之所有关于文档中提到的关于表达式的内容,做一个汇总以及梳理,让我清晰,全面,直观,深刻地理解相关内容
回答1:
以下是两个文档中关于表达式核心内容的系统化梳理,采用结构化方式呈现:
表达式知识体系
一、三种表达式形式对比
| 类型 | 结构 | 示例 | 特点 | 计算顺序 |
|---|---|---|---|---|
| 中缀表达式 | 运算符在操作数中间 | a + b * (c - d) | 需要括号和优先级规则 | 依赖运算符优先级和结合性 |
| 前缀表达式 | 运算符在操作数前 | + a * b - c d | 无需括号,适合递归处理 | 从右向左扫描,运算符优先执行 |
| 后缀表达式 | 运算符在操作数后 | a b c d - * + | 无需括号,适合栈计算 | 从左向右扫描,遇运算符立即计算 |
二、表达式转换核心方法
1. 中缀转后缀(重点)
转换步骤:
- 加完全括号:明确运算优先级
a + b * c → (a + (b * c)) - 移动运算符:将运算符移到对应括号后
(a (b c *) +) → abc*+ - 去除括号:得到后缀表达式
abc*+
栈算法流程:
优先级规则表:
| 运算符 | 栈内优先级 | 栈外优先级 | 说明 |
|---|---|---|---|
( | 1 | 8 | 强制入栈 |
) | - | 1 | 强制出栈 |
* / % | 5 | 4 | 高优先级 |
+ - | 3 | 2 | 低优先级 |
# | 0 | - | 栈底标记 |
示例:1 + 2 * 3 → 1 2 3 * +
2. 中缀转前缀
转换步骤:
- 加完全括号:
a + b * c → (a + (b * c)) - 移动运算符:将运算符移到对应括号前
+ a * b c - 去除括号:得到前缀表达式
+ a * b c
三、表达式计算方法
1. 后缀表达式计算(栈实现)
算法步骤:
- 初始化空栈
- 从左到右扫描后缀表达式:
- 操作数:入栈
- 运算符:弹出栈顶两个操作数计算,结果入栈
- 最终栈顶为计算结果
示例:3 4 2 * 1 5 - / +
计算过程:
3 → 栈 [3]
4 → 栈 [3,4]
2 → 栈 [3,4,2]
* → 4*2=8 → 栈 [3,8]
1 → 栈 [3,8,1]
5 → 栈 [3,8,1,5]
- → 1-5=-4 → 栈 [3,8,-4]
/ → 8/-4=-2 → 栈 [3,-2]
+ → 3+(-2)=1 → 结果 1
2. 中缀表达式计算(双栈法)
- 操作数栈:存储数值
- 运算符栈:存储运算符
- 当遇到运算符时,与栈顶比较优先级,按需弹出计算
回答2:
这次我们抛开所有数学符号和理论,用最直观的认知映射和人类本能直觉来彻底打通这三大表达式。准备好迎接「啊哈时刻」!
终极生活类比(3秒懂核心)
-
中缀表达式:做菜步骤说明书
- “先炒鸡蛋(等油热),然后加西红柿(但要先切块)”
- 需要不断看优先级(先切菜还是先热油?)
-
前缀表达式:军事指令
- “全体注意!现在执行:开火→瞄准→目标A”
- 必须倒着执行:先找到目标A,再瞄准,最后开火
-
后缀表达式:快递分拣流水线
- “包裹北京→包裹上海→合并发华北区”
- 看到什么就立刻处理什么,绝不回头
灵魂三问(人类本能验证法)
Q1:为什么计算机讨厌中缀表达式?
→ 就像让外国人看中文菜谱:
3 + 5 × 2
人类秒懂先乘后加,但计算机需要反复扫描确认优先级(像查字典)
Q2:后缀表达式为何高效?
→ 如同工厂流水线:
3 5 2 × +
工人(CPU)只需低头处理眼前物品:
- 拿3 → 放桌上
- 拿5 → 放桌上
- 拿2 → 放桌上
- 看到× → 把最后两个相乘 → 得到10放桌上
- 看到+ → 把最后两个相加 → 结束
全程不用抬头看优先级!
Q3:前缀表达式存在的意义?
→ 像组装宜家家具的步骤:
× + 3 5 2
必须从右往左读:
- 先找到2
- 再找到5
- 执行+ → 3+5=8
- 最后执行× → 8×2=16
适合递归处理(函数式编程的DNA)
手动转换术(不背算法,用自然思维)
目标:把中缀表达式 (3+5)×2 转为后缀
-
画出计算顺序:
×/ \+ 2/ \3 5 -
(树根是×,左子树是+,右子树是2)
-
后序遍历这棵树:
- 先访问左子树(+):3 → 5 → +
- 再访问右子树(2)
- 最后访问根节点(×)
→ 3 5 + 2 ×
-
终极验证:
想象你是计算机,按顺序处理:
3入栈 →5入栈 →弹出5+3=8入栈 →2入栈 →弹出2×8=16
脑内成像训练(闭眼想象)
-
中缀:迷宫路线图(需要自己找出口)
A + B × C - D
→ 你要自己决定先走×通道还是+通道 -
后缀:直梯楼层按钮
A B C × + D -
→ 严格从下往上点亮按钮,绝不跳层 -
前缀:俄罗斯套娃
- + A × B C D
→ 必须从最外层娃娃开始拆解
暴击式总结
-
后缀表达式 = 即时满足模式
(看到运算符就立刻结算,绝不拖延) -
前缀表达式 = 战略规划模式
(先部署所有操作指令,再反向执行) -
中缀表达式 = 人类谈判现场
(需要不断协调优先级和括号)
现在试着重写这个式子:(6-3)/(2+4×5)
用「快递流水线思维」转换为后缀表达式,感受那种「不用动脑,直接流水线操作」的快感!
(答案:6 3 - 2 4 5 × + / → 像传送带上的包裹一样逐个处理)
回答3:
我用最简洁、高密度的方式将前缀、中缀、后缀表达式的核心逻辑提炼给你:
三大表达式核心对比表
| 中缀 | 前缀(波兰) | 后缀(逆波兰) | |
|---|---|---|---|
| 结构 | 操作符在操作数中间 | 操作符在操作数前 | 操作符在操作数后 |
| 示例 | (A+B)*C | *+ABC | AB+C* |
| 括号 | 必须 | 完全不需要 | 完全不需要 |
| 计算 | 需优先级判断 | 严格从左到右解析 | 严格从左到右计算 |
| 用途 | 人类阅读 | Lisp类语法/编译器 | 计算机高效计算 |
顶级理解三连击
-
本质差异
- 中缀表达式是人类视角,用括号和优先级模拟计算顺序
- 前缀/后缀是机器视角,通过操作符位置隐式表达计算顺序
-
转换核心算法
-
中缀→后缀:用栈缓存操作符(遇高优先级弹出低优先级)
# 例:A+B*C → ABC*+ # 栈操作流程:+遇到*时因优先级低被压栈,*运算完弹出+ -
中缀→前缀:反转表达式→处理后缀→再反转
(需处理操作数顺序,复杂度更高)
-
-
求值终极方案
-
后缀计算:遇到操作数压栈,遇到操作符弹出栈顶两元素计算
# 计算 AB+C* (即 (A+B)*C ) # 栈演变:A → A,B → (A+B) → (A+B),C → (A+B)*C -
前缀计算:从右向左扫描,其他逻辑与后缀类似
-
深度认知突破
-
为什么栈是关键?
表达式本质是操作符优先级嵌套结构,栈完美匹配这种"后进先出"的嵌套关系 -
逆波兰为何高效?
消除了括号和优先级判断,计算时只需单次线性扫描(时间复杂度O(n)) -
现实应用场景:
- 编译器语法解析(Abstract Syntax Tree构建)
- 金融交易系统的实时报价计算
- 老式HP计算器的工作原理
终极验证方法
用这个表达式检验是否真正理解:
中缀:3*(4^2+10/5)-6
→ 前缀:- * 3 + ^ 4 2 / 10 5 6
→ 后缀:3 4 2 ^ 10 5 / + * 6 -
(计算顺序:4²=16 → 10/5=2 → 16+2=18 → 3×18=54 → 54-6=48)
AI模型版本:
中国的深度求索(DeepSeek)公司开发的智能助手DeepSeek-V3
采用深度思考模式,深度思考模型版本为R1
没有打开联网搜索
对话编号:2
相关文章:

Day36【AI思考】-表达式知识体系总览
文章目录 **表达式知识体系总览**回答1:**表达式知识体系****一、三种表达式形式对比****二、表达式转换核心方法****1. 中缀转后缀(重点)****2. 中缀转前缀** **三、表达式计算方法****1. 后缀表达式计算(栈实现)****…...
调试)
段错误(Segmentation Fault)调试
1. 使用 GDB(GNU Debugger) GDB 是一个强大的调试工具,可以帮助你逐步执行程序并检查变量状态。 编译时添加调试信息: gcc -g your_program.c -o your_program启动 GDB: gdb ./your_program运行程序: …...
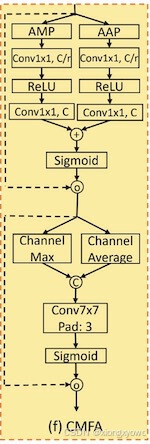
每日Attention学习19——Convolutional Multi-Focal Attention
每日Attention学习19——Convolutional Multi-Focal Attention 模块出处 [ICLR 25 Submission] [link] UltraLightUNet: Rethinking U-shaped Network with Multi-kernel Lightweight Convolutions for Medical Image Segmentation 模块名称 Convolutional Multi-Focal Atte…...

LeetCode题练习与总结:三个数的最大乘积--628
一、题目描述 给你一个整型数组 nums ,在数组中找出由三个数组成的最大乘积,并输出这个乘积。 示例 1: 输入:nums [1,2,3] 输出:6示例 2: 输入:nums [1,2,3,4] 输出:24示例 3&a…...

Colorful/七彩虹 隐星P15 TA 24 原厂Win11 家庭版系统 带F9 Colorful一键恢复功能
Colorful/七彩虹 隐星P15 TA 24 原厂Win11 家庭中文版系统 带F9 Colorful一键恢复功能 自动重建COLORFUL RECOVERY功能 带所有随机软件和机型专用驱动 支持机型:隐星P15 TA 24 文件下载:asusoem.cn/745.html 文件格式:ISO 系统版本&…...

第二篇:多模态技术突破——DeepSeek如何重构AI的感知与认知边界
——从跨模态对齐到因果推理的工程化实践 在AI技术从单一模态向多模态跃迁的关键阶段,DeepSeek通过自研的多模态融合框架,在视觉-语言-语音的联合理解与生成领域实现系统性突破。本文将从技术实现层面,解构其跨模态表征学习、动态融合机制与…...

CTreeCtrl 设置图标
mfc界面修改真难受 使用CTreeCtrl 进行设置导航视图时,有时候需要设置图标,一般使用如下代码 m_TreeViewImages.DeleteImageList();UINT uiBmpId IDB_ICONLIST_TREE;CBitmap bmp; if (!bmp.LoadBitmap(uiBmpId)) return;BITMAP bmpObj; bmp.GetBitmap…...

在JAX-RS中获取请求头信息的方法
在JAX-RS中获取请求头信息的方法 HeaderParam注解,可以直接将请求头中的特定值注入到方法参数中,代码示例: import javax.ws.rs.GET; import javax.ws.rs.HeaderParam; import javax.ws.rs.Path; import javax.ws.rs.core.Response;Path(&q…...

Java 面试之结束问答
技术优化 线程池优化 设置最大线程数设置最小核心线程数设置额外线程存活时间选择线程池队列选择合适的线程池选择合适的饱和策略 锁优化 尽量不要锁住方法缩小同步代码块,只锁数据锁中尽量不要再包含锁将锁私有化,在内部管理锁进行适当的锁分解 HT…...
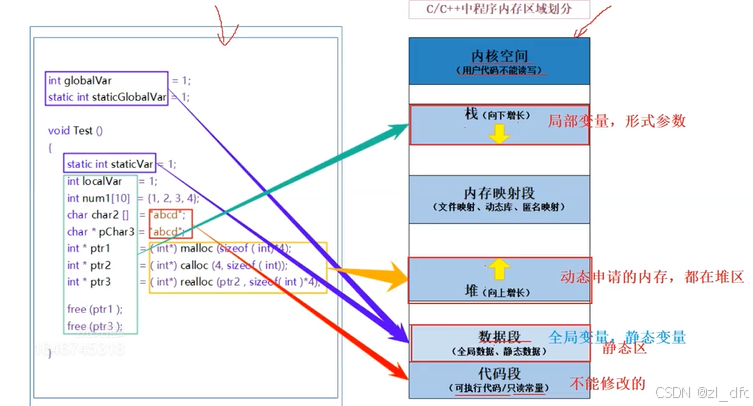
柔性数组与c/c++程序中内存区域的划分
1.柔性数组 1.1柔性数组的定义 柔性数组是指在结构体中定义的,其大小在编译时未确定,而在运行时动态分配的数组。这种数组允许结构体的大小根据需要动态变化。语法如下: struct D {int a;int arry1[0]; };struct F {int a;int arry2[]; };…...

mini-lsm通关笔记Week2Day7
项目地址:https://github.com/skyzh/mini-lsm 个人实现地址:https://gitee.com/cnyuyang/mini-lsm 在上一章中,您已经构建了一个完整的基于LSM的存储引擎。在本周末,我们将实现存储引擎的一些简单但重要的优化。欢迎来到Mini-LSM的…...
Typora免费使用
一.下载地址 https://typoraio.cn/ 二.修改配置文件 1.找到安装路径下的LicenseIndex.180dd4c7.4da8909c.chunk.js文件 文件路径为:安装路径\resources\page-dist\static\js\LicenseIndex.180dd4c7.4da8909c.chunk.js 将js中的 e.hasActivated"true"e.hasActiva…...
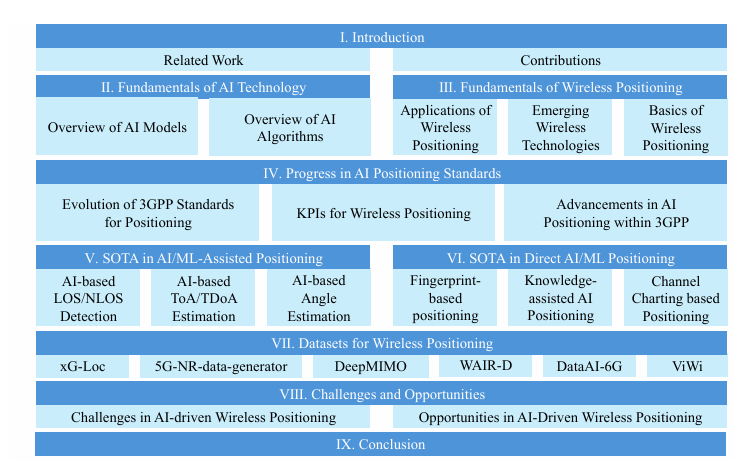
AI驱动的无线定位:基础、标准、最新进展与挑战
1. 论文概述 研究目标:本论文旨在综述AI在无线定位领域的应用,包括其基础理论、标准化进展、最新技术发展,以及面临的挑战和未来研究方向。主要发现: AI/ML 技术已成为提升无线定位精度和鲁棒性的关键手段,特别是在 3GPP 标准的推动下。论文系统性地分析了 AI 在 LOS/NLOS…...

苹果再度砍掉AR眼镜项目?AR真的是伪风口吗?
曾经,AR游戏一度异常火热,宝可梦go让多少人不惜翻墙都要去玩,但是也没过去几年,苹果被曝出再度砍掉了AR眼镜项目,面对着市场的变化,让人不禁想问AR真的是伪风口吗? 一、苹果再度砍掉AR眼镜项目&…...
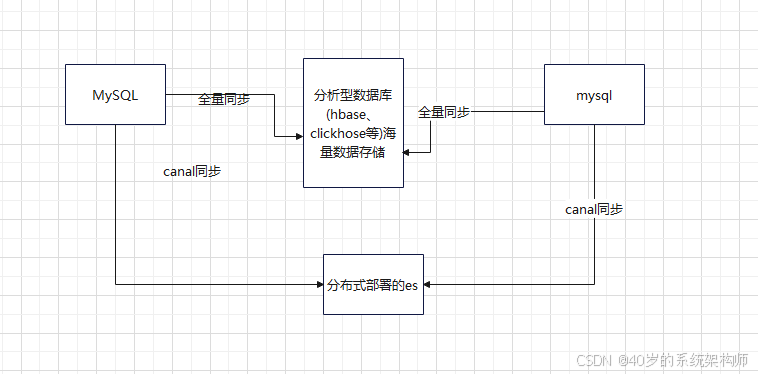
18 大量数据的异步查询方案
在分布式的应用中分库分表大家都已经熟知了。如果我们的程序中需要做一个模糊查询,那就涉及到跨库搜索的情况,这个时候需要看中间件能不能支持跨库求交集的功能。比如mycat就不支持跨库查询,当然现在mycat也渐渐被摒弃了(没有处理笛卡尔交集的…...
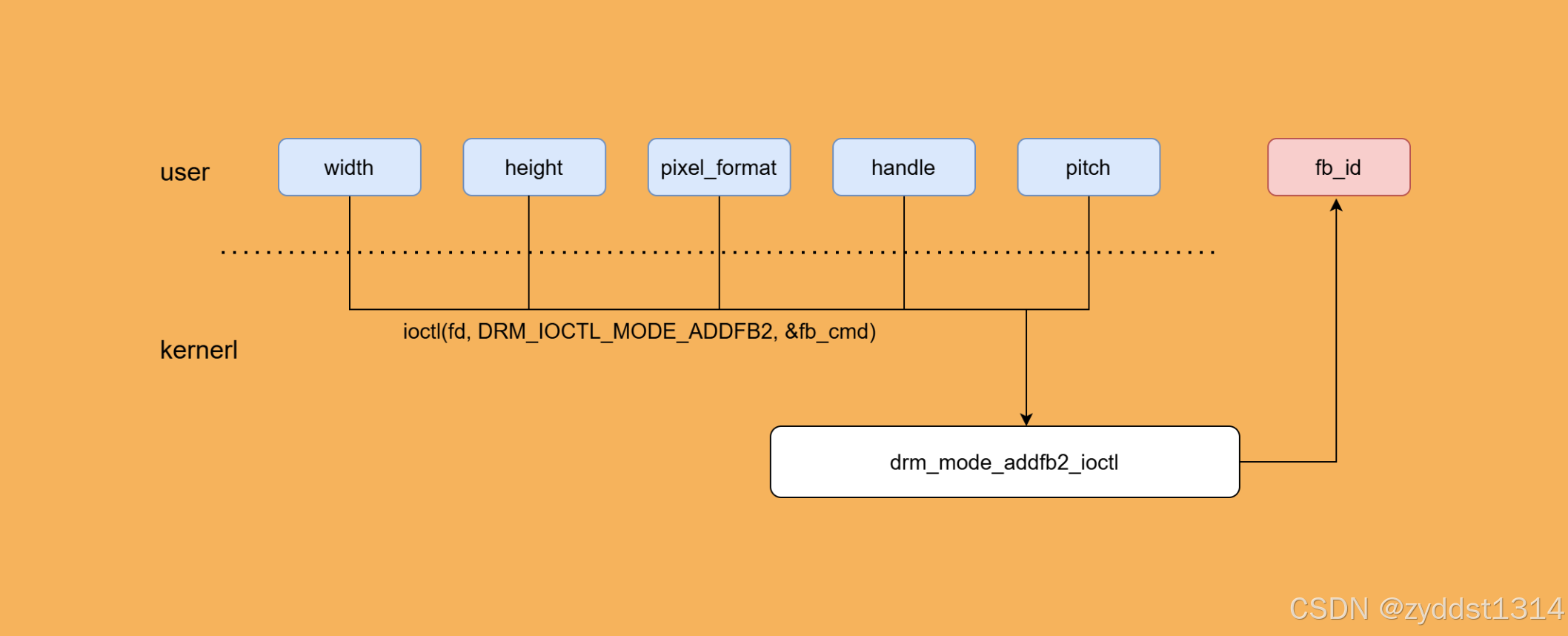
DRM系列八:Drm之DRM_IOCTL_MODE_ADDFB2
本系列文章基于linux 5.15 在上一篇文章DRM系列七:Drm之DRM_IOCTL_MODE_CREATE_DUMB获取buf的handle和pitch之后,接着使用ioctl(fd, DRM_IOCTL_MODE_ADDFB2, &fb_cmd)创建一个新的帧缓冲区对象(framebuffer object),并将帧缓冲区对象与显…...
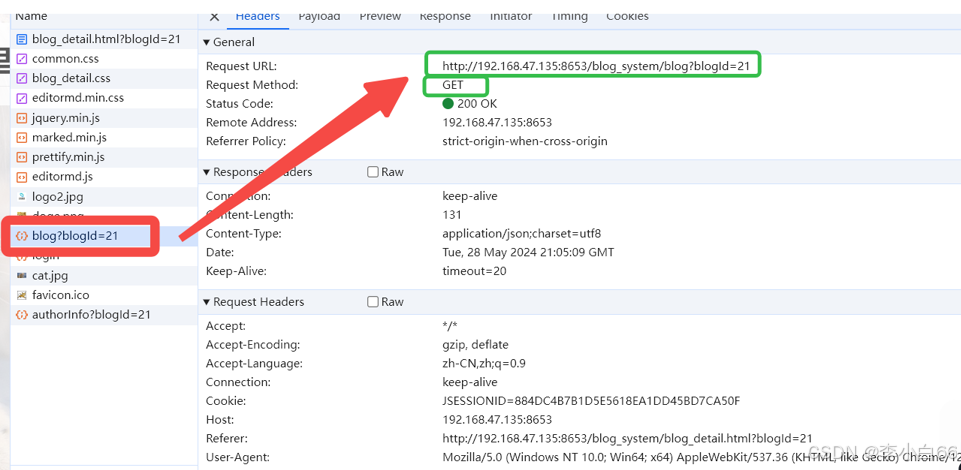
软件测试用例篇
设计测试用例是测试面试的必考题,务必好好学 1. 测试用例 测试用例的概念 测试⽤例(Test Case)是为了实施测试而向被测试的系统提供的⼀组集合,这组集合包含:测试环境、操作步骤、测试数据、预期结果等要素。 设计测试⽤…...

PopupMenuButton组件的功能和用法
文章目录 1 概念介绍2 使用方法3 示例代码 我们在上一章回中介绍了Sliver综合示例相关的内容,本章回中将介绍PopupMenuButton组件.闲话休提,让我们一起Talk Flutter吧。 1 概念介绍 我们在本章回中介绍的PopupMenuButton组件位于AppBar右侧,…...

Python进行模型优化与调参
在数据科学与机器学习领域,模型的优化与调参是提高模型性能的重要步骤之一。模型优化可以帮助提高模型的准确性和泛化能力,而合理的调参则能够充分发挥模型的潜力。这篇教程将重点介绍几种常用的模型优化与调参方法,特别是超参数调整和正则化技术的应用。这些技术能够有效地…...
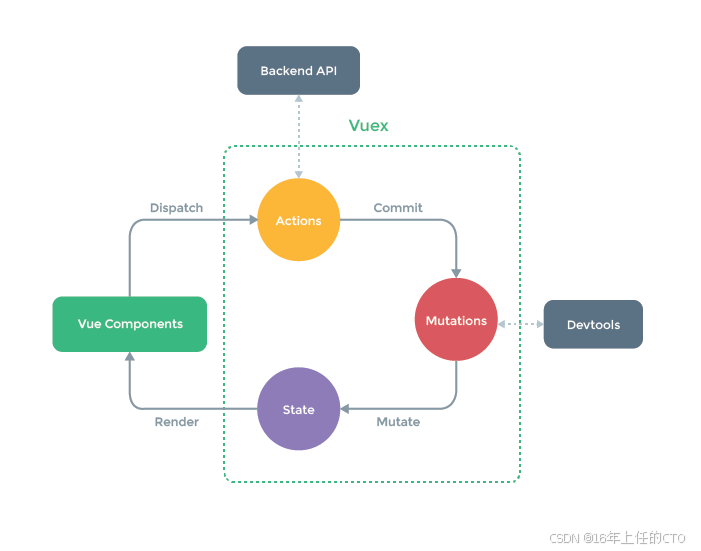
vue2-组件通信
文章目录 vue2-组件通信1. 为什么需要组件通信2. props传递数据3. $emit触发自定义事件4.ref5. EventBus6. p a r e n t 和 parent和 parent和root7. a t t r s 和 attrs和 attrs和listeners8. provide和inject9. vuex10. 总结 vue2-组件通信 1. 为什么需要组件通信 在VUE中…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
